Espressioni con angoli associati: ESERCIZI SVOLTI

Espressioni con angoli associati: ESERCIZI SVOLTI! In questa pagina vediamo esercizi svolti sugli angoli associati. Vedremo inoltre un trucchetto per non imparare a memoria la tabella degli angoli associati! Vediamo poi come utilizzare tali formule per semplificare le espressioni, iniziamo subito!

Indice

• Angoli associati tabella
• Come NON imparare a memoria la tabella
• Espressioni goniometriche con angoli associati

Lasciamo qui giù la tabella di formule di angoli associati, che ci servirà per risolvere gli esercizi di espressioni sugli angoli associati.

---

Angoli associati TABELLA

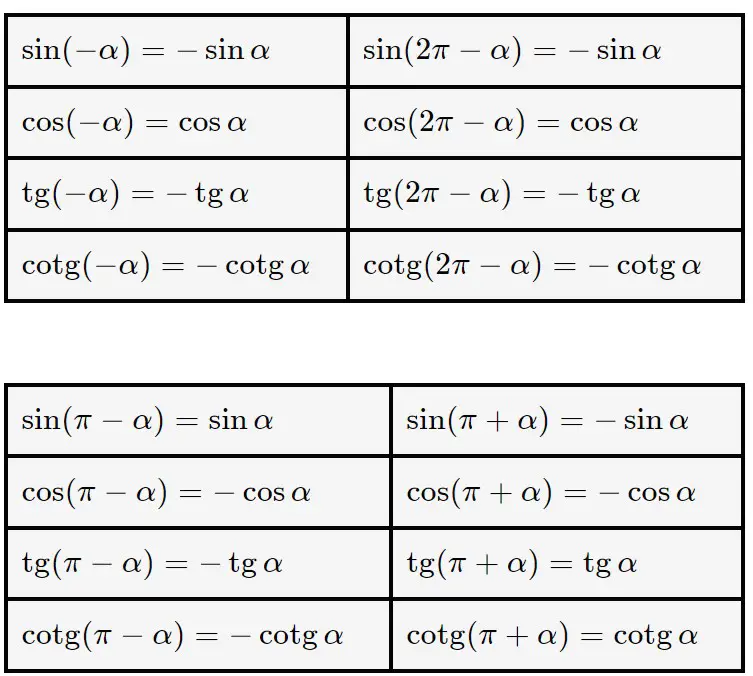
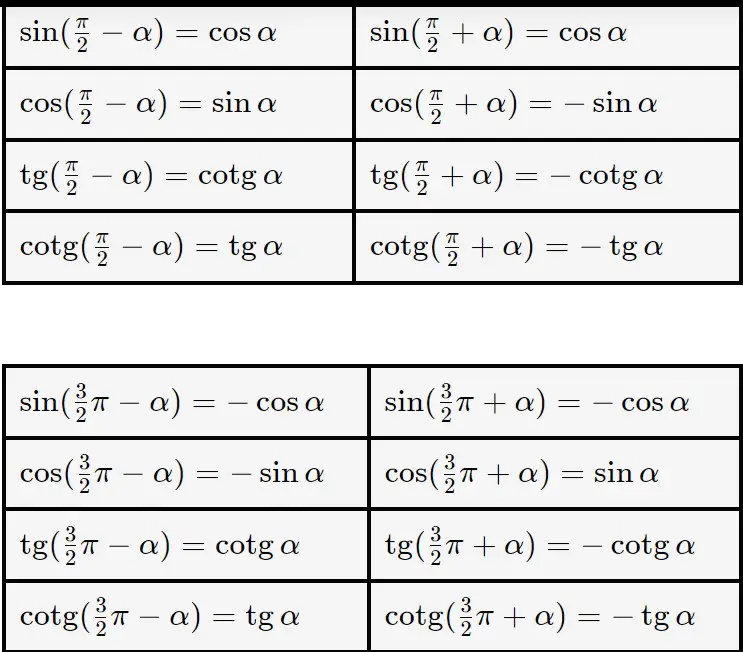
Questa tabella sarà utilissima soprattutto durante la verifica in classe! Ma come fare se non c’è possibilità di averla davanti o di copiarla? In questa sezione vedremo un trucchetto per ricavare qualsiasi formula della tabella a momento, senza troppe difficoltà!

Come NON imparare a memoria la tabella

Adesso vediamo una cosa utilissima, che non c’è scritta quasi da nessuna parte sul web! Tutte le formule di angoli associati sopra scritta possono essere ricavate a momento. Adesso vediamo come fare.

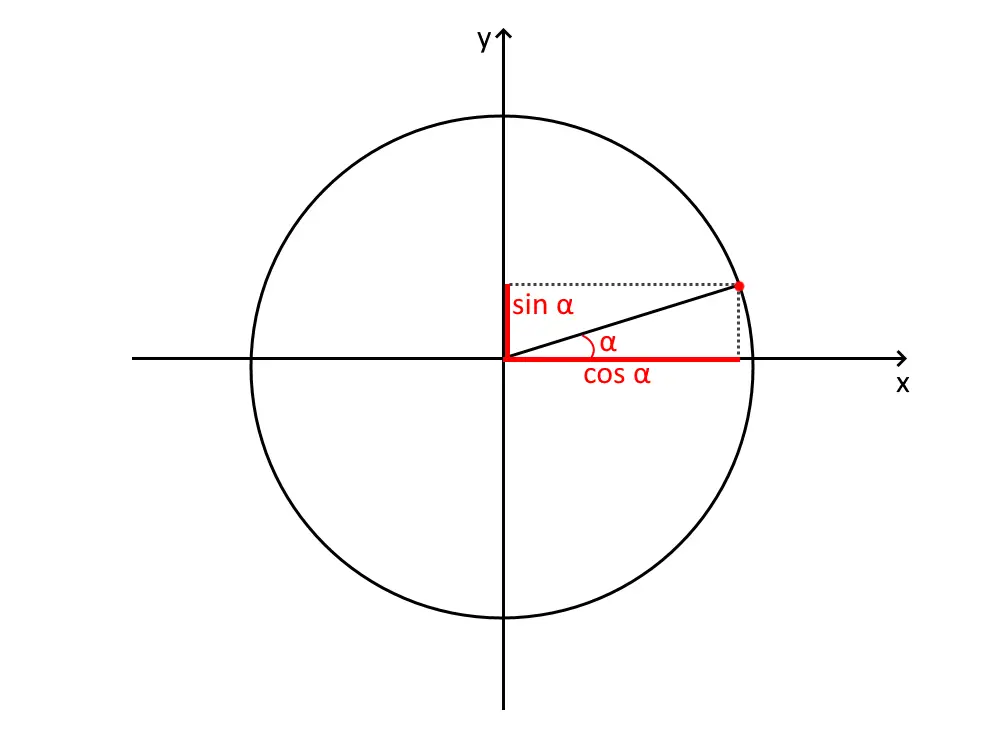
La prima cosa da fare è disegnare un angolo piccolino nel primo quadrante, come segue. Questo sarà l’angolo $\alpha$. E’ importante che sia piccolo, altrimenti ci si potrebbe confondere dopo. Proiettiamo sugli assi poi il punto che si interseca con la circonferenza goniometrica: in questo modo abbiamo il suo seno ed il suo coseno.

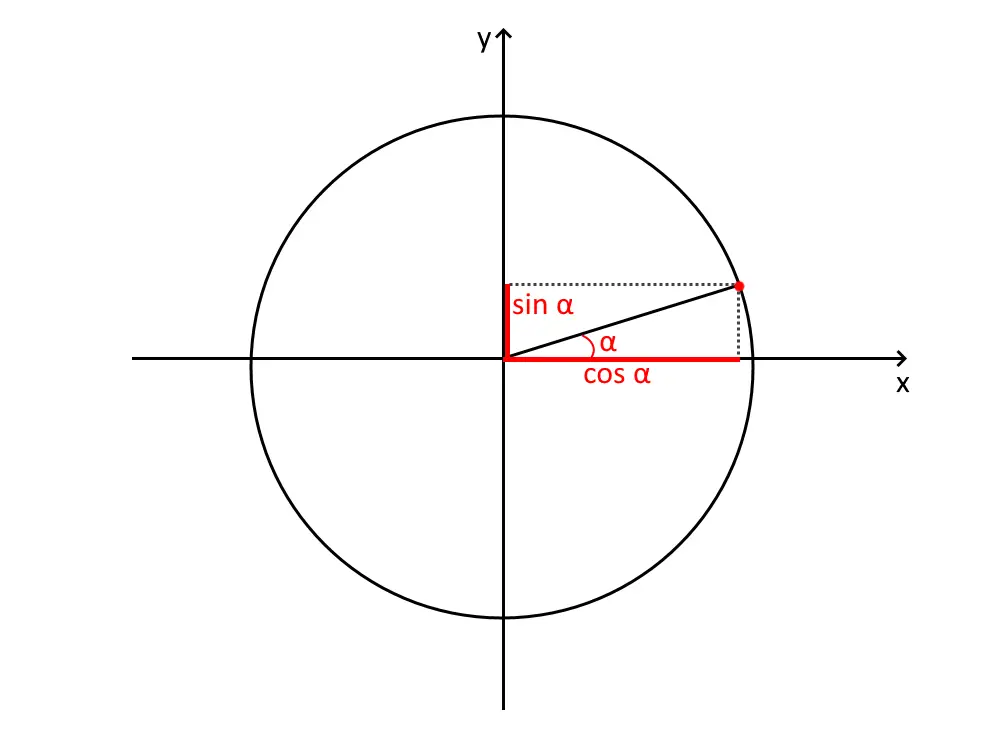
Adesso vediamo cosa ci chiede l’esercizio. Supponiamo che nell’esercizio ci sia scritto:

$\cos (\pi + \alpha) = ?$

Per ricavare ad esempio questo angolo associato, il secondo punto è: disegnare l’angolo che sta scritto nell’esercizio, quindi qui ad esempio è $\pi + \alpha$. L’esercizio ci chiede il coseno di questo angolo, quindi proiettiamo solamente il suo coseno, cioè la proiezione sull’asse x.

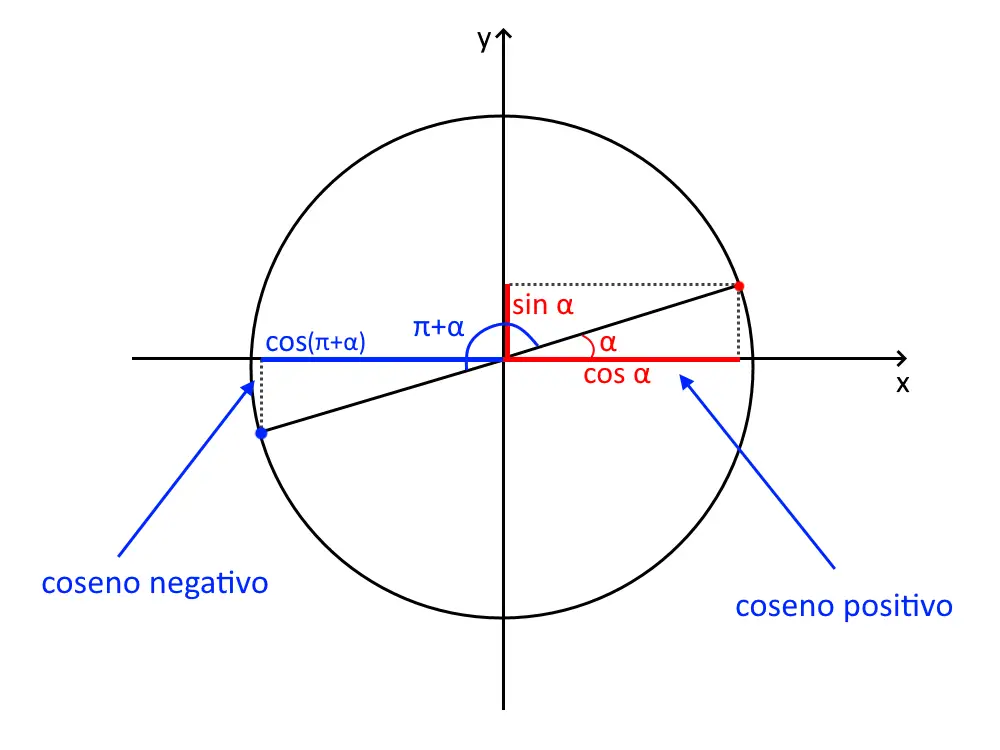
Questo coseno lo disegniamo col rosso, ed è questo che vogliamo sapere. Ora vediamo semplicemente quale lato rosso è uguale al coseno di $\pi + \alpha$. Notiamo che il lato uguale è quello relativo al $\cos \alpha$.

Adesso dobbiamo vedere il segno: notiamo che uno è negativo e l’altro è positivo. Quindi la formula dell’angolo associato sarà:

$\cos (\pi + \alpha) = - \cos \alpha$

Ecco fatto!

Vediamo un altro esempio, nell’espressione goniometrica supponiamo ci sia scritto:

$\sin (\frac{\pi}{2} + \alpha ) = ?$

Il procedimento è sempre lo stesso: disegniamo la circonferenza goniometrica, un angolo piccolino nel primo quadrante, e poi vi proiettiamo il suo seno ed il suo coseno.

Ora il secondo punto è disegnare l’angolo $\frac{\pi}{2} + \alpha$. Poi l’esercizio ci chiede il suo seno, quindi proiettiamo solo il suo seno, ossia sull’asse y.

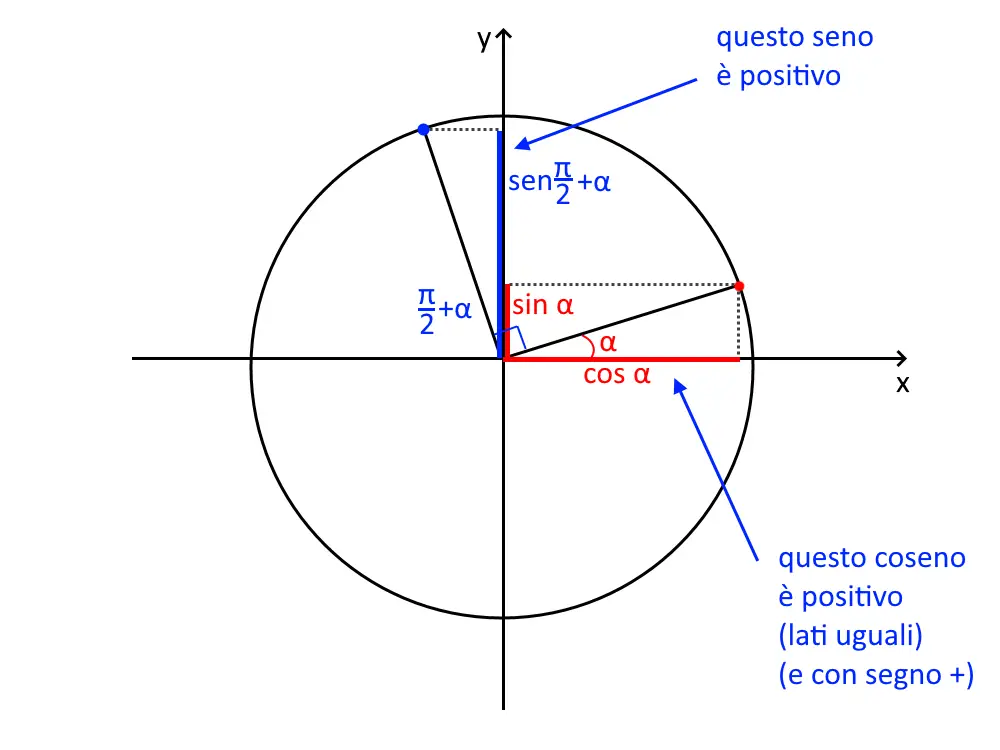
Adesso dobbiamo vedere quale lato rosso è uguale a quello blu. Notiamo che il lato rosso relativo al coseno dell’angolo alfa è uguale. Quindi questa è la relazione di uguaglianza. Ora dobbiamo vedere se i segni coincidono: tutti e due questi lati sono positivi. Quindi il segno da mettere nella relazione è +, quindi la formula goniometrica dell’angolo associato sarà:

$\sin (\frac{\pi}{2} + \alpha ) = \cos \alpha$

Ora vediamo un ultimo esempio con la cotangente questa volta. Supponiamo che nell’espressione ci sia scritto:

$\cotg (\frac{\pi}{2} + \alpha ) = ?$

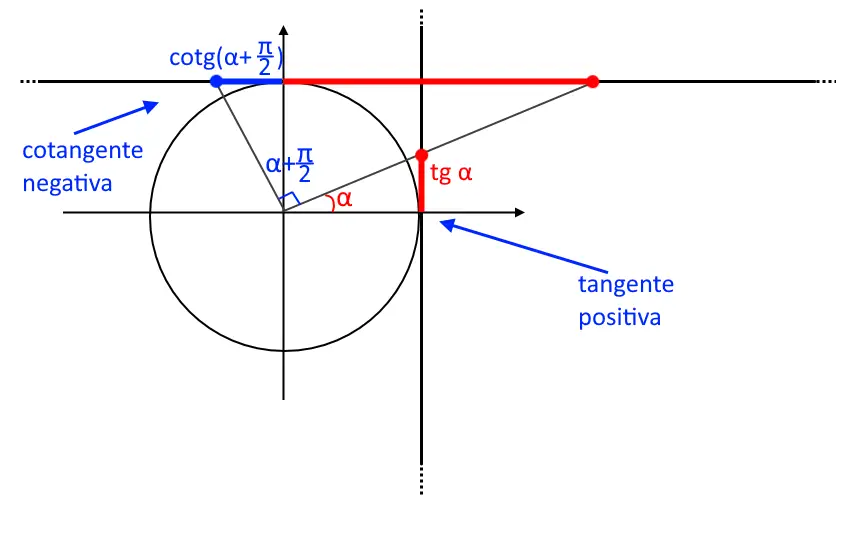
Ricordate che la tangente è legata con la cotangente e viceversa. Quindi andiamo a disegnare sempre l’angolo piccolino, e poi proiettiamo tale sulla cotangente questa volta, e anche sulla tangente!

Ora disegniamo l’angolo $\frac{\pi}{2} + \alpha$. L’esercizio vuole sapere la cotangente, quindi proiettiamo tale valore solo sulla cotangente chiaramente. Notiamo che tale lato blu è piccolo: il lato rosso uguale è quello relativo alla tangente! Adesso dobbiamo vedere i segni: uno è positivo, e l’altro è negativo, quindi nella formula dobbiamo mettere un segno meno! La formula di angolo associato è quindi:

$\cotg (\frac{\pi}{2} + \alpha ) = - \tg \alpha$

Ora vediamo come applicare le formule goniometriche degli angoli associati in espressioni nei nostri esercizi svolti e spiegati!

ESPRESSIONI goniometriche con angoli associati
esercizi svolti

Riassumiamo qui gli esercizi modello, quelli da fare assolutamente:

• Esercizio 1
• Esercizio 4
• Esercizio 5
• Esercizio 6
• Esercizio 7

---

Esercizio 1. $\cos (-\alpha ) + \cos (360° - \alpha ) + \cos (180° - \alpha) - \cos (180° + \alpha )$


Per non confonderci, il primo passaggio sarà di scrivere tutto in radianti, visto che le formule degli angoli associati sono in radianti. Se volete potete saltare questo passaggio. Per ciò basta ricordarci che i valori degli angoli più importanti:

$\begin{cases} 90° = \frac{\pi}{2} \\ 180° = \pi \\ 270° = \frac{3}{2}\pi \\ 360° = 2\pi \end{cases}$

Quindi la nostra espressione assume una forma più consona alle formule che dobbiamo utilizzare!

$\cos (-\alpha ) + \cos (2\pi - \alpha ) + \cos (\pi - \alpha) - \cos (\pi + \alpha )$

E a questo punto basta vedere nella tabella le formule necessarie, una ad una. Se siete durante una verifica e non avete modo di vedere la tabella di tutti gli archi associati, basta vedere la sezione precedente, che spiega come ricavare tutte le formule con facilità, senza imparare a memoria nulla!

Applicando le formule:

$\implies \cos \alpha + \cos \alpha - \cos \alpha - (-\cos \alpha )$

Nell’ultimo termine, essendoci già un segno meno davanti, è sempre meglio mettere le parentesi! I segni negativi sono sempre tediosi, quindi mettete le parentesi per sicurezza!

$\implies \cos \alpha + \cos \alpha - \cos \alpha + \cos \alpha$

Sommiamo i termini di coseno, come se fossero dei termini algebrici normali:

$\implies 2\cos \alpha$

E l’espressione è stata semplificata! L’esercizio è finito quindi.

Esercizio 2. $\sin (90° + \alpha ) \tg (- \alpha) + \sin (90° + \alpha ) \cotg (90° - \alpha) - \cos ( - \alpha) \sin (90° - \alpha )$


Per comodità, la prima cosa che andiamo a fare è scrivere tutti gli angoli in radianti, così spiccano all’occhio subito le formule da usare!

$\sin (\frac{\pi}{2} + \alpha ) \tg (- \alpha) + \sin (\frac{\pi}{2} + \alpha ) \cotg (\frac{\pi}{2} - \alpha) - \cos ( - \alpha) \sin (\frac{\pi}{2} - \alpha )$

Vediamo nella tabella/ricaviamole a momento, ed applichiamo tali formule, ricordando sempre di mettere le parentesi soprattutto quando ci sono dei segni negativi.

$\cos \alpha \cdotp (- \tg \alpha) + \cos \alpha \cdotp \tg \alpha - \cos \alpha \cdotp \cos \alpha$

Leviamo la parentesi e mettiamo il segno meglio scritto:

$- \cos \alpha \cdotp \tg \alpha) + \cos \alpha \cdotp \tg \alpha - \cos \alpha \cdotp \cos \alpha$

L’obiettivo di questi esercizi è sempre quello di semplificare il più possibile l’espressione goniometrica! Lo possiamo fare ricordando la definizione di tangente!

$\tg \alpha = \frac{\sin \alpha }{\cos \alpha }$

L’ultimo pezzo inoltre è in pratica il coseno al quadrato:

$- \cos \alpha \frac{\sin \alpha }{\cos \alpha } + \cos \alpha \frac{\sin \alpha }{\cos \alpha } - \cos^2 \alpha$

Semplifichiamo i coseni delle frazioni, visto che uno sta al numeratore ed uno al denominatore in pratica.

$- \sin \alpha + \sin \alpha - \cos^2 \alpha$

Il seno se ne va, essendo due seni uguali ed opposti di segno, e quindi il risultato dell’esercizio è:

$\implies - \cos^2 \alpha$

Esercizio 3. $\frac{\sin ( - \alpha ) + \cos (180° - \alpha) - \tg (180° + \alpha) }{\tg (180° - \alpha) - \cos (90° - \alpha ) - \cos (- \alpha) }$


Qui abbiamo una frazione, diversamente dagli scorsi esercizi: il succo non cambia, usiamo le formule degli archi associati al numeratore, ed al denominatore. Alla fine ci aspettiamo qualche messa in evidenza, o semplificazioni fra numeratore e denominatore. Scriviamo innanzitutto in radianti:

$\frac{\sin ( - \alpha ) + \cos (\pi - \alpha) - \tg (\pi + \alpha) }{\tg (\pi - \alpha) - \cos (\frac{\pi}{2} - \alpha ) - \cos (- \alpha) }$

Di conseguenza ricaviamo:

$\frac{-\sin \alpha - \cos \alpha - \tg \alpha }{-\tg \alpha - \sin \alpha - \cos \alpha }$

Prima di pensare di scrivere la tangente attraverso la sua definizione, e poi fare un minimo comune multiplo…osserviamo bene la frazione! Il numeratore è esattamente uguale al denominatore: hanno gli stessi 3 termini, e quindi possiamo semplificare direttamente ed ottenere come risultato:

$\implies 1$

Continuiamo con altre espressioni con angoli associati esercizi svolti!

Esercizio 4. $\sin (\frac{3}{2}\pi -\alpha ) + \cos (3\pi + \alpha ) + \sin ( - \alpha) \cotg ( \alpha -5\pi )$


Il primo termine è chiaramente un angolo associato. Ma per gli altri come facciamo? Vista la periodicità degli angoli nella circonferenza goniometrica, possiamo sfruttarla per riscrivere gli angoli in una forma diversa.

Quando gli angoli sono più grandi di $2\pi = 360°$ possiamo riscrivere l’angolo andando a sottrarre di volta in volta $2\pi$ finché non si arriva ad un angolo noto. Ad esempio nella nostra espressione abbiamo nel coseno $3\pi$, e facciamo come segue:

$3\pi = 3\pi - 2\pi = \pi$

E questo è lo stesso identico angolo, ma facendo un giro in meno in pratica. Ed è la stessa identica cosa! Quindi ricapitolando, sottraiamo di volta in volta 360°.

Per l’altro poi:

$5\pi = 5\pi - 2\pi = 3\pi$

E di nuovo: $3\pi - 2\pi = \pi$

Quindi l’espressione si trasforma in una forma molto più semplice ed intuitiva, con un semplice passaggio!

$\sin (\frac{3}{2}\pi -\alpha ) + \cos (\pi + \alpha ) + \sin ( - \alpha) \cotg ( \alpha -\pi )$

Considerando le relazioni degli angoli associati, ricaviamo che:

$- \cos \alpha - \cos \alpha - \sin \alpha \cdotp \cotg ( \alpha -\pi )$

L’ultimo NON è un angolo associato, perché come vedete gli angoli associati sono della forma inversa, cioè:

cotg (angolo – alfa)

In questi casi si mette un segno meno in evidenza all’interno dell’angolo della cotangente:

$- \cos \alpha - \cos \alpha - \sin \alpha \cdotp \cotg [-( \pi - \alpha )]$

A questo punto prendiamo da parte la cotangente un attimo.

$\cotg [-( \pi - \alpha )]$

Poniamo un attimo $\pi - \alpha = \beta$

$\implies \cotg [- \beta ]$

Vediamo negli angoli associati (la denominazione di alfa o beta non cambia nulla) e segue che:

$\cotg [- \beta ] =- \cotg \beta$

Ed ora risostituiamo ed otteniamo quindi:

$- \cotg \beta = - \cotg (\pi - \alpha )$

Ed ora l’espressione ha anche la cotangente come angolo associato!

$- \cos \alpha - \cos \alpha - \sin \alpha \cdotp - \cotg (\pi - \alpha )$

$- \cos \alpha - \cos \alpha - \sin \alpha \cdotp + \cotg \alpha$

L’ultimo segno diventa:

$- \cos \alpha - \cos \alpha - \sin \alpha \cotg \alpha$

Adesso sì che non possiamo fare null’altro, quindi utilizziamo la definizione di cotangente, e sommiamo i primi due termini uguali di coseno:

$- 2\cos \alpha - \sin \alpha \frac{ \cos \alpha }{ \sin \alpha}$

Semplifichiamo col denominatore e ricaviamo:

$- 2\cos \alpha - \cos \alpha = -3 \cos \alpha$

Esercizio 5. $\sin (\alpha -2\pi) \cotg (- \alpha ) + \sin ( \alpha + \frac{3}{2}\pi ) \cos ( \alpha +5\pi) + \sin^2 (6\pi - \alpha)$


Ci sono molti angoli strani, quindi non mettiamo mano direttamente tutto in una volta sull’espressione, ma vediamoli uno per uno con calma. Partiamo dal primo seno che non è un angolo associato (perché alfa deve stare a destra):

$\sin (\alpha -2\pi) = \sin [ - ( 2\pi - \alpha ) ] = \sin (- \beta )$

E come fatto prima, in pratica mettiamo in evidenza un segno meno dentro l’angolo, e poi lo rinominiamo beta, e da lì possiamo usare la formula dell’angolo associato del seno:

$\sin (- \beta ) = - \sin \beta = -\sin (2\pi - \alpha)$

Ed ora lo abbiamo trasformato in angolo associato! L’altro seno va bene perché l’addizione è commutativa:

$\sin ( \alpha + \frac{3}{2}\pi ) = \sin ( \frac{3}{2}\pi + \alpha )$

Passiamo all’analisi del coseno adesso. Come già visto abbiamo un angolo più grande di $2\pi$, e quindi dobbiamo andare a sottrarre valori di $2\pi$ fino a che non arriviamo ad un angolo comune:

$5\pi = 5 \pi - 2\pi - 2\pi = \pi$

Per l’ultimo seno il discorso è uguale! Ed allora:

$6\pi = 6 \pi - 2\pi - 2\pi = 2\pi$

Sostituiamo il tutto nella nostra espressione, ora notevolmente più semplificata!

$-\sin (2\pi - \alpha) \cotg (- \alpha ) + \sin ( \frac{3}{2}\pi +\alpha ) \cos ( \pi + \alpha ) + \sin^2 (2\pi - \alpha)$

L’ultimo seno è elevato al quadrato, quindi stacchiamolo! E così la formula appare in maniera naturale:

$-\sin (2\pi - \alpha) \cotg (- \alpha ) + \sin ( \frac{3}{2}\pi +\alpha ) \cos ( \pi + \alpha ) + \sin (2\pi - \alpha) \cdotp \sin (2\pi - \alpha)$

Applichiamo le formule degli angoli associati (grande attenzione ai SEGNI):

$- \cdotp -\sin \alpha \cdotp -\cotg \alpha - \cos \alpha \cdotp - \cos \alpha - \sin \alpha \cdotp - \sin \alpha$

Mettiamo i segni apposto come si deve!

$- \sin \alpha \cotg \alpha + \cos \alpha \cos \alpha + \sin \alpha \sin \alpha$

$- \sin \alpha \cotg \alpha + \cos^2 \alpha + \sin^2 \alpha$

Usiamo la definizione di cotangente ora:

$- \sin \alpha \frac{\cos \alpha }{\sin \alpha } + \cos^2 \alpha + \sin^2 \alpha$

$-\cos \alpha + \cos^2 \alpha + \sin^2 \alpha$

Ricordando la prima relazione fondamentale della goniometria, abbiamo una espressione ancora più compatta:

$-\cos \alpha +1$

Continuiamo con altre espressioni con angoli associati esercizi svolti!

Esercizio 6. $\cos (-\alpha ) \sin (\frac{5}{2}\pi + \alpha ) + \sin (\frac{7}{2}\pi - \alpha) \cotg (\frac{\pi}{2} + \alpha ) + \sin (\frac{\pi}{2} + \alpha ) \tg (\pi - \alpha)$


Osserviamo l’espressione goniometrica e individuiamo prima tutti i termini non immediatamente riconducibili a angolo associati. Partiamo proprio dal primo seno, che ha un angolo più grande di $2 \pi$. Anche se la frazione può spaventare, non cambia nulla: sottraiamo sempre per $2 \pi$:

$\frac{5}{2}\pi = \frac{5}{2}\pi - 2\pi = \frac{5\pi - 4 \pi }{2} = \frac{\pi}{2}$

E stessa identica cosa per l’altro seno, cui c’è bisogno di sottrarre sempre una volta, per arrivare ad un angolo comune.

$\frac{7}{2}\pi = \frac{7}{2}\pi - 2\pi = \frac{7\pi - 4 \pi }{2} = \frac{3}{2}\pi$

Abbiamo finito, possiamo quindi riscrivere l’espressione in questa forma più semplice:

$\cos (-\alpha ) \sin (\frac{\pi}{2} + \alpha ) + \sin (\frac{3}{2}\pi - \alpha) \cotg (\frac{\pi}{2} + \alpha ) + \sin (\frac{\pi}{2} + \alpha ) \tg (\pi - \alpha)$

Applichiamo le formule degli archi associati ed otteniamo perciò:

$\cos \alpha \cos \alpha - \cos \alpha \cdotp - \tg \alpha + \cos \alpha \cdotp - \tg \alpha$

Riscriviamo in una forma più umana i segni dell’espressione.

$\cos \alpha \cos \alpha + \cos \alpha \tg \alpha - \cos \alpha \tg \alpha$

Il primo è un coseno quadro in pratica, poi gli altri due termini sono uguali ed opposti, e quindi si cancellano! Il risultato è quindi:

$\implies \cos^2 \alpha$

Esercizio 7. $-\cos (-\alpha - \frac{3}{2} \pi ) - \sin ( \alpha - 5\pi) + \sin ( - \alpha - \frac{7}{2} \pi )$


Come sempre osserviamo prima l’espressione goniometrica che il libro o la professoressa ci dà e riflettiamoci un attimo. Il primo coseno ha un angolo strano, analizziamolo e riscriviamolo mettendo un segno meno in evidenza dentro il coseno:

$\cos (-\alpha - \frac{3}{2} \pi ) = \cos - ( \alpha + \frac{3}{2} \pi ) = \cos (- \beta )$

Abbiamo fatto comparire uno dei primi angoli associati, quindi il coseno di meno beta diventa:

$\cos (- \beta ) = \cos \beta = \cos ( \alpha + \frac{3}{2} \pi )$

Ed abbiamo fatto con questo coseno. Poi abbiamo un seno con un angolo più grande, e alfa che dovrebbe stare a sinistra. Allora, una cosa alla volta, ricordiamo che:

$5\pi = 5\pi -2 \pi - 2 \pi = \pi$

$\implies \sin ( \alpha - 5\pi) = \sin ( \alpha - \pi) = \sin - (\pi - \alpha)$

Poniamo tale angolo in beta, e sfruttiamo l’angolo associato del seno:

$\implies \sin - \beta = - \sin \beta = - \sin (\pi - \alpha)$

Anche l’ultimo seno richiede un discorso analogo, se non uguale in pratica. Riscriviamo innanzitutto l’angolo più grande come:

$\frac{7}{2} \pi = \frac{7}{2} \pi - 2 \pi = \frac{7 \pi - 4 \pi}{2} = \frac{3}{2} \pi$

Ed allora iniziamo a sostituire questo e poi:

$\sin ( - \alpha - \frac{3}{2} \pi ) = \sin - (\alpha + \frac{3}{2} \pi) = \sin ( - \beta )$

$\implies \sin ( - \beta ) = - \sin \beta = - \sin (\alpha + \frac{3}{2} \pi)$

Abbiamo tutto riscritto in termini family-friendly delle formule goniometriche in una forma che ci piace tanto! Ora l’espressione quindi viene riscritta come:

$-\cos ( \alpha + \frac{3}{2} \pi ) - \cdotp - \sin (\pi - \alpha) - \sin (\alpha + \frac{3}{2} \pi)$

$-\cos ( \alpha + \frac{3}{2} \pi ) + \sin (\pi - \alpha) - \sin (\alpha + \frac{3}{2} \pi)$

Usiamo le amatissime formule ormai:

$\sin \alpha + \sin \alpha - \cos \alpha = 2 \sin \alpha - \cos \alpha$

---

In questa pagina abbiamo visto come ricavare da soli le formule degli archi associati, e abbiamo visto esercizi svolti su espressioni goniometriche semplificabili utilizzando tali formule. Il prossimo step è risolvere espressioni con formule goniometriche, poi le identità goniometriche!

Continuate a studiare sul nostro sito: trovate altre centinaia di esercizi svolti sia di matematica che altro ancora!



Per approfondire:
https://it.wikipedia.org/wiki/Trigonometria

Espressioni goniometriche con angoli associati esercizi svolti

Espressioni
con angoli
associati