La FORMULA del PENDOLO è SBAGLIATA!

Il pendolo, il famoso pendolo! Viene studiato per anni al Liceo, e poi ripreso all’Università! Il pendolo è in pratica composto da una pallina di una certa massa, cui è posto in un piano verticale ad un punto tramite un filo di lunghezza L.

La formula che abbiamo sempre usato per il periodo del pendolo è:

T = 2 \pi \sqrt{\frac{L}{g} }

Guardiamo bene questa formula e commentiamola per capire perché questa è sbagliata nella realtà e non funziona!

Abbiamo 2 \pi che è una costante, poi abbiamo l’accelerazione di gravità g che anch’essa è una costante (è vero che in montagna è diversa dalla pianura, ma facciamo finta che sia pari ad un valore costante per semplicità). Quindi l’unica variabile del periodo del pendolo è L, la lunghezza del filo.

Ciò significa che facendo variare SOLO la lunghezza del filo VARIA il periodo del pendolo (ossia quanto ci mette per fare sinistra-destra in pratica). Ma qualcosa non torna!

Perché non torna? Se noi facessimo partire il pendolo ad un’ampiezza iniziale \theta_0 piccola come a sinistra, o con un’ampiezza iniziale molto più grande come a destra, allora non cambia nulla? Il periodo è sempre uguale? Ci mette lo stesso tempo? Beh dovete sapere che se provate a fare degli esperimenti, capirete che non è uguale. E quindi la formula non è corretta.

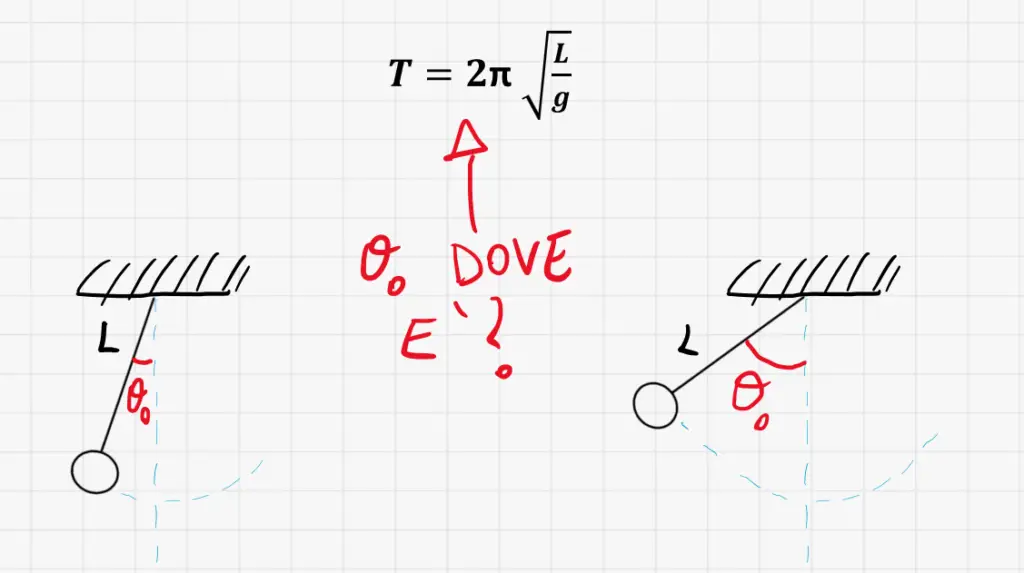
Ma allora perché usiamo questa? Da dove esce? Partiamo prima col darvi la formula più precisa in assoluto:

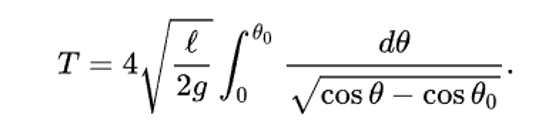
Come possiamo vedere compare ora \theta_0 ! Eccolo! Ora…siamo capaci di usarla? No, ovviamente. Anzi, non è un integrale qualsiasi, è anche molto difficile da risolvere. Di conseguenza al Liceo non possiamo di certo usare questa formula, e nemmeno all’Università! Di fatti questo lo si risolve con metodi super avanzati.

La formula a noi nota allora da dove esce?

Per chi vuol vedere qualche calcolino, eccovi a voi. Ma non ci soffermeremo troppo, altrimenti ci annoiamo tutti!

Concentrandoci sulla dinamica che avviene tangente al moto, si ha:

m a_t = - mg \sin \theta

Usando poi la definizione di accelerazione angolare, ossia tale che:

a_t = L \frac{d^2 \theta}{dt^2}

Si ha che l’equazione da risolvere per ottenere informazioni sul moto è:

\frac{d^2 \theta}{dt^2} + \frac{g}{L} \sin \theta = 0

Il problema è che questa è davvero super complicata da risolvere, anche con metodi di primi anni universitari. Quindi si escogita un metodo per arrivare comunque ad una formula accettabile e approssimata. Ossia andiamo a considerare piccoli angoli!

Consideriamo quindi \theta << 1rad

E chi è questo 1rad? A cosa corrisponde? Beh, possiamo fare questo ragionamento seguente. Se \pi = 3.14 che corrisponde a 180°, allora 1 corrisponderà a 57° circa (una semplice proporzione).

E allora andiamo a sviluppare il seno, perché è quello il problema. Se ci fosse solo l’angolo, allora sarebbe una equazione differenziale di secondo ordine omogenea di cui sappiamo la soluzione. Ed allora sviluppiamo:

\sin \theta \approx \theta - \frac{\theta^3}{3!} +...

E decidiamo di fermarci al primo ordine. Di conseguenza la nuova equazione approssimata è:

\frac{d^2 \theta}{dt^2} + \frac{g}{L} \theta = 0

Che ora sappiamo risolvere! E che ci porterà alla famosa formula che conosciamo del pendolo!

Approssimata, ma che significa?

Abbiamo ricavato la formula approssimata del pendolo, o meglio del suo periodo, ma cosa significa questo? Vale? In che range vale?

Allora, la formula è stata ricavata, andando a considerare angoli:

\theta << 1rad

Abbiamo capito che \theta = 1 corrispondevano 57°, ed ora quindi:

57° << 1

Quando si scrive questo, ossia “molto più piccolo di”, si intende un ordine di grandezza di differenza almeno. Di conseguenza vogliamo intendere angoli più piccoli di 5,7°!

La formula vale quindi per angoli più piccoli di tale quantità! Però facciamo un altro po’ di chiarezza!

La formula, come sempre capita in Fisica, non è precisa al 100%. Più vi si avvicina con un’ampiezza iniziale che tende a 0° e più l’errore relativo si avvicina a 0, e la formula è precisa.

A 5,7° di ampiezza iniziale si ha un errore relativo di 10^{-3} , che è comunque piccolissimo! Ma è chiaro che se vogliamo misure ancora più precise già ora abbiamo dei problemi!

Più diventa grande l’angolo e più l’errore su tale formula sarà grande! Di conseguenza ad angoli di 50° o 80° la formula è super imprecisa. Ci darà quindi valori diversi da quelli osservati nella realtà. E qui entra in gioco l’altra formula.

Ma è chiaro che, piuttosto che non studiare tale argomento, si preferisce ovviamente usare quella formula, che è molto semplice per tutti.