Teorema di Pitagora FORMULA e DIMOSTRAZIONE
Teorema di Pitagora: FORMULA e DIMOSTRAZIONE! In questa pagina vedremo l’enunciato del Teorema di Pitagora, la sua formula e come la si dimostra. Poi vedremo alcuni problemi svolti e diverse applicazioni (come quella in un triangolo isoscele): in questo modo sarete preparati a qualsiasi evenienza nella verifica in classe! Iniziamo subito!
Indice
- Teorema di Pitagora: formula
- Dimostrazione del Teorema di Pitagora
- Teorema di Pitagora: triangolo isoscele
- Teorema di Pitagora: triangolo equilatero
- Problemi
Concetti base
Prima di iniziare ripetiamo alcuni concetti base che ci serviranno:
- Triangolo rettangolo: è un triangolo che ha un angolo retto, ossia di 90°;
- Ipotenusa: è il lato più grande di un triangolo;
- Cateto minore: è il lato più piccolo di un triangolo;
- Cateto maggiore: è l’ultimo lato.
Iniziamo subito ad enunciare il Teorema di Pitagora, e a vederne le formule!
Teorema di Pitagora: formula
Enunciato: In un triangolo rettangolo, il quadrato costruito sull’ipotenusa ha l’Area uguale alla somma delle Aree degli altri due quadrati costruiti sui cateti.
Cosa significa questo in parole povere?
In pratica prendiamo un triangolo rettangolo (ossia con un angolo retto, di 90°) e ci disegniamo su ogni lato un quadrato, abbiamo la figura seguente.
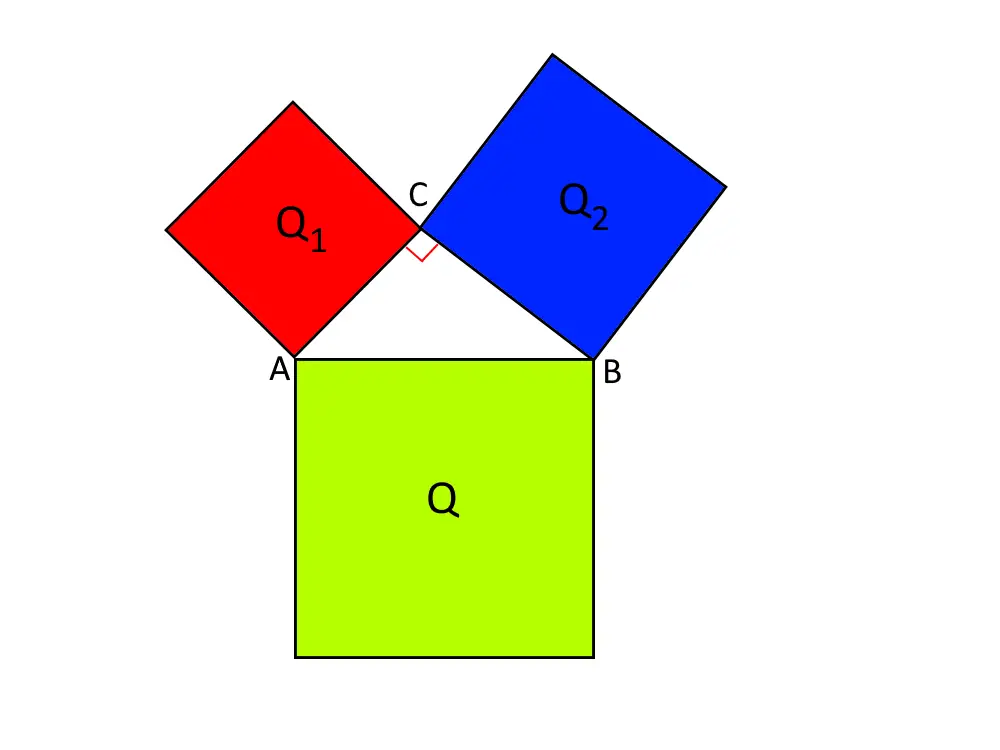
Una volta fatto questo piccolo giochetto, Pitagora misurò l’Area di ogni singolo quadrato e scoprì una cosa: l’Area del quadrato più grande (cioè quello che ha come lato l’ipotenusa) è proprio esattamente uguale alle altre due Aree sommate fra di loro:
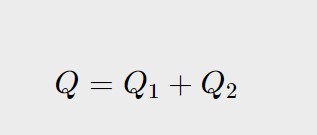
E questa è la prima importante formula!
A questo punto ricordiamoci un attimo la formula per calcolare l’Area di un Quadrato qualsiasi:
A = l \cdotp l = l^2
Grazie proprio a questa formula possiamo riscrivere in una forma diversa questa:
Q=Q_1 + Q_2
Iniziamo a calcolare l’Area del quadrato più grande. Chiamiamo con la lettera i l’ipotenusa del triangolo (che come vedete dal disegno è proprio anche il lato del quadrato Q!). L’Area di Q è:
Q= i \cdotp i = i^2
Adesso calcoliamo l’Area del quadrato Q_1 che ha come lato il cateto minore c del triangolo.
Q_1= c \cdotp c = c^2
Adesso ci rimane da calcolare l’Area del quadrato Q_2 che ha come lato il cateto maggiore C del triangolo.
Q_2= C \cdotp C = C^2
Abbiamo calcolato l’Area di tutti e 3 i quadrati. Adesso ritorniamo alla formula che Pitagora trovò, ossia:
Q=Q_1 + Q_2
Ora che conosciamo le tre Aree possiamo sostituire i risultati ottenuti! Visto che:
- Q=i^2
- Q_1=c^2
- Q_2=C^2
Sostituiamo e otteniamo la nuova formula:
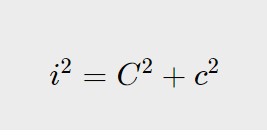
Come potete vedere questa formula lega assieme, grazie a questa relazione, tutti e 3 i lati di un triangolo. Partendo proprio da questa formula possiamo calcolare ogni singolo lato, conoscendo gli altri due: vediamo come!
Calcoliamo l’ipotenusa di un triangolo: per fare ciò facciamo la radice quadrata ad entrambi i membri! Otteniamo:
\sqrt{i^2}=\sqrt{C^2 + c^2}
La radice del primo termine, grazie ad una proprietà delle potenze e radici, si semplifica col quadrato dell’ipotenusa ed otteniamo quindi:
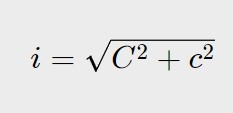
Grazie a questa formula possiamo calcolare la lunghezza dell’ipotenusa di un triangolo, solamente conoscendo la lunghezza degli altri due cateti!
Adesso proviamo invece a calcolare la lunghezza del cateto maggiore C. Partiamo sempre dalla formula iniziale:
i^2=C^2 + c^2
Portiamo il termine C^2 a primo membro (ricordatevi che in una equazione quando si cambia lato bisogna anche cambiare di segno poi):
-C^2 + i^2=c^2
Ora portiamo l’ipotenusa a secondo membro:
-C^2 =-i^2 + c^2
Cambiamo tutto di segno adesso, perché vogliamo il cateto maggiore C positivo (visto che poi dovremmo fare la radice dopo):
C^2 =i^2 - c^2
Ed otteniamo questo! Ora possiamo come prima fare la radice quadrata ad ambo i membri. La radice è per definizione positiva o uguale a zero, ed è per questo che vogliamo il primo termine positivo ed abbiamo cambiato tutto di segno! Quindi applichiamo la radice quadrata ed otteniamo:
\sqrt{C^2} =\sqrt{i^2 - c^2}
Il primo termine, come detto prima, fa semplificare il quadrato con la radice e quindi otteniamo questa nuova formula:
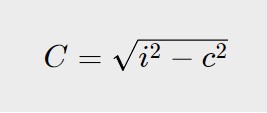
Questa qui sopra ci permette di calcolare la lunghezza del cateto maggiore C, solamente conoscendo la lunghezza questa volta dell’ipotenusa e del cateto minore c. State attenti che a differenza di prima qui c’è un segno meno!
Adesso ci rimane da calcolare il cateto minore c. Partiamo sempre dalla formula iniziale:
i^2=C^2 + c^2
Portiamo il cateto minore a primo membro (non dimenticatevi di cambiare segno):
-c^2 + i^2=C^2
Adesso portiamo l’ipotenusa a secondo membro:
-c^2 =-i^2 + C^2
Ora, per il discorso fatto prima (ossia che visto che dobbiamo fare la radice vogliamo tutto positivo) cambiamo tutto di segno:
c^2 =i^2 - C^2
Adesso, possiamo fare la radice ad ambo i membri ed otteniamo:
\sqrt{c^2} =\sqrt{ i^2 - C^2 }
Nel primo termine radice e quadrato si semplificano, per una proprietà delle potenze e radici. Quindi otteniamo una nuova formula:
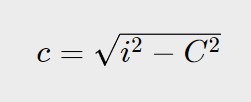
Questa ci permette di calcolare la lunghezza del cateto minore c, solo conoscendo la lunghezza dell’ipotenusa e del cateto maggiore!
Abbiamo trovato tutte le formule che ci servono grazie al Teorema di Pitagora!
Dimostrazione Teorema di Pitagora
Nel capitolo precedente abbiamo enunciato il Teorema di Pitagora che dice che: in un triangolo rettangolo, il quadrato costruito sull’ipotenusa ha l’Area uguale alla somma delle Aree degli altri due quadrati costruiti sui cateti.
E siamo arrivati alla conseguente formula:
Q=Q_1 + Q_2
E’ proprio questo quindi quello che vogliamo dimostrare con i calcoli!
Prendendo lo stesso disegno di prima, quindi quello col triangolo rettangolo ed i quadrati disegnati, prolunghiamo l’altezza \overline{AH} del triangolo rettangolo, fino a che non divide il quadrato Q in due.
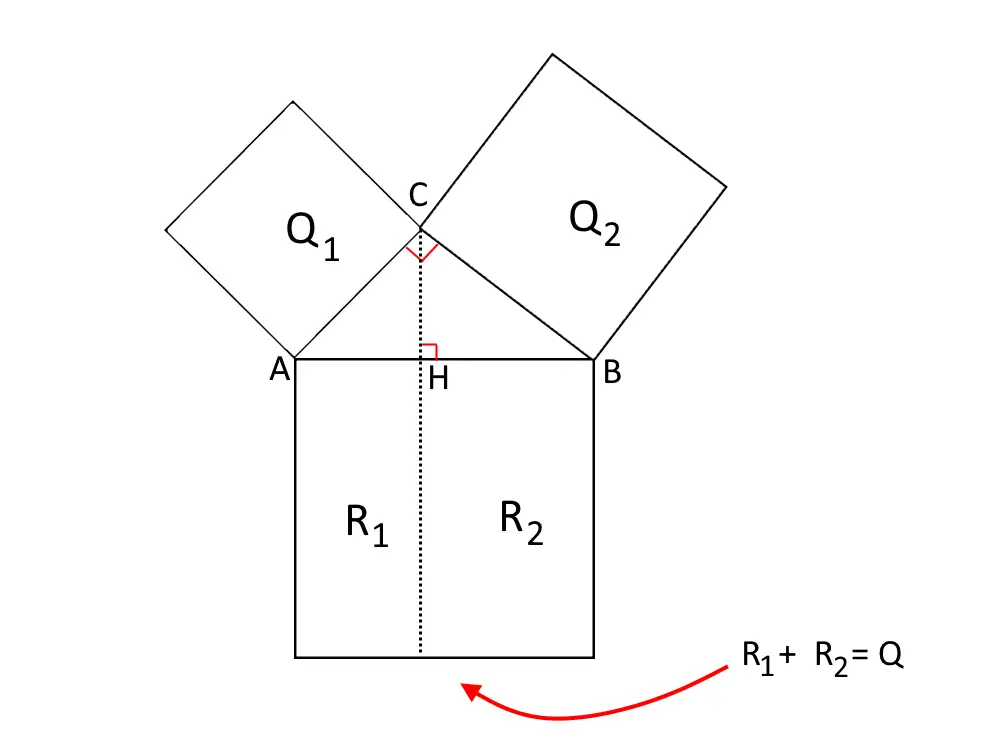
Il quadrato Q è diviso, come vedete dal disegno, in due rettangoli R_1 ed R_2.
Il primo Teorema di Euclide ci dice che:
- L’area del quadrato Q_1 è uguale a quella del rettangolo R_1
- L’area del quadrato Q_2 è uguale a quella del rettangolo R_2
In breve:
\begin{cases} Q_1 = R_1 \\ Q_2 = R_2 \end{cases}
Adesso sommiamo membro a membro (ossia sommiamo i membri di sinistra fra di loro e poi quelli di destra fra di loro). Viene fuori:
Q_1 + Q_2 = R_1 + R_2
I due rettangoli non sono nient’altro che il quadrato Q divido in due. Quindi ovviamente l’area del primo rettangolo sommata all’area del secondo rettangolo mi ritorna a dare il quadrato iniziale Q! Cioè in formule:
Q= R_1 + R_2
Questa relazione la sostituiamo nella seguente:
Q_1 + Q_2 = R_1 + R_2
Quindi adesso sostituiamo:
Q_1 + Q_2 = Q
Ed abbiamo così dimostrato e ricavato ciò che dice il Teorema di Pitagora e la sua formula!
(se volete sapere come ricavare l’ipotenusa, cateto maggiore e cateto minore sono state fatte nel capitolo precedente)
Teorema di Pitagora: triangolo isoscele
Vediamo adesso come si può applicare il Teorema di Pitagora ad un triangolo che non è rettangolo! Ma bensì isoscele. Ripetiamo che un triangolo isoscele è: un triangolo che ha due lati e due angoli uguali.
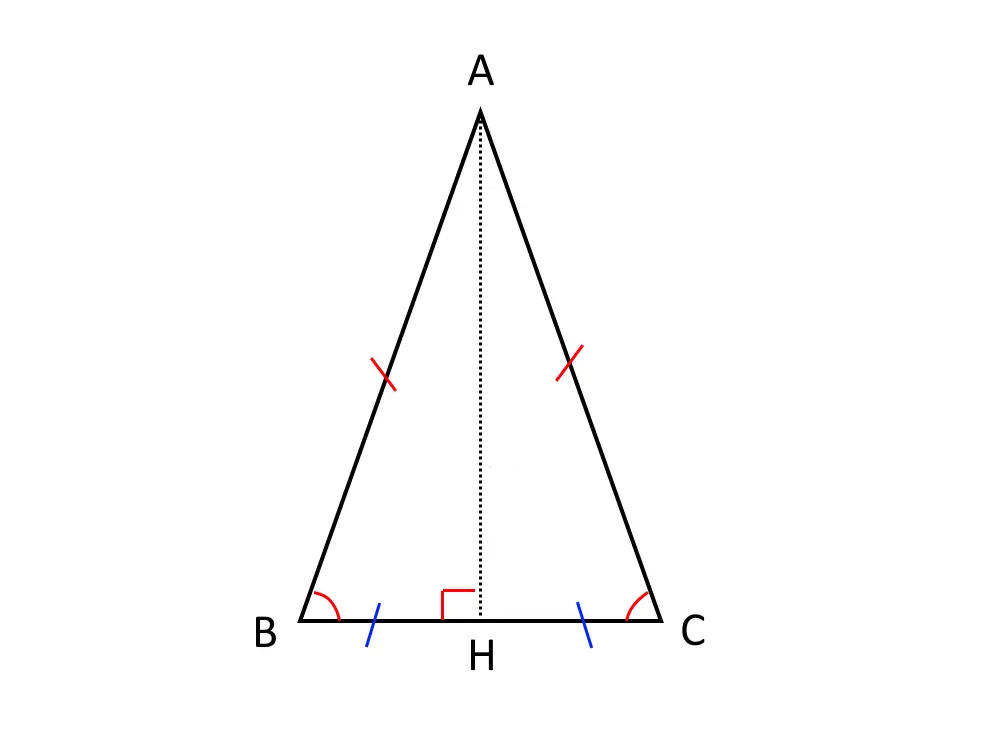
Il Teorema di Pitagora però si può applicare SOLAMENTE ad un triangolo rettangolo! Quindi come facciamo? Ciò che facciamo è tracciare l’altezza \overline{AH} del triangolo isoscele, e come vedete taglia esattamente a metà la base del triangolo.
Quindi si sono creati due triangoli rettangoli uguali! Ossia:
Il triangolo ABH ed il triangolo AHC, entrambi rettangoli.
Quindi adesso possiamo applicare il Teorema di Pitagora, ed usare le sue formule, solamente però a questi due triangoli rettangoli.
Determiniamo la lunghezza dell’altezza del triangolo isoscele, conoscendo i tre lati, ed utilizziamo il Teorema di Pitagora.
I due triangoli rettangoli creatosi sono uguali, quindi scegliamo ad esempio di fare i calcoli con il triangolo ABH. In questo triangolo rettangolo ABH abbiamo che:
- \overline{AH} è il cateto maggiore del triangolo ABH;
- \overline{BH} è il cateto minore del triangolo ABH;
- \overline{AB} è l’ipotenusa del triangolo ABH;
Visto che vogliamo calcolare l’altezza del triangolo isoscele \overline{AH} che è il cateto maggiore del triangolo ABH, allora utilizziamo la formula del Teorema di Pitagora per calcolare il cateto maggiore di un triangolo rettangolo:
C =\sqrt{ i^2 - c^2 }
Nel nostro caso:
C= \overline{AH}
i=\overline{AB}
c= \overline{BH} = \frac{\overline{BC} }{2}
Sostituiamo questi dati nella formula ed otteniamo:
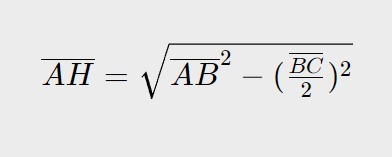
Quindi ricapitolando ciò che abbiamo visto in questo capitolo: possiamo utilizzare il Teorema di Pitagora in un triangolo isoscele tracciando l’altezza e quindi creando così due triangoli rettangoli!
Teorema di Pitagora:
triangolo equilatero
Il Teorema di Pitagora si può applicare, come dice l’enunciato, SOLO per un triangolo rettangolo. Se abbiamo un triangolo equilatero (ossia un triangolo con 3 lati e 3 angoli uguali) allora come facciamo? Il procedimento che adottiamo è esattamente lo stesso fatto nel capitoletto precedente per un triangolo isoscele.
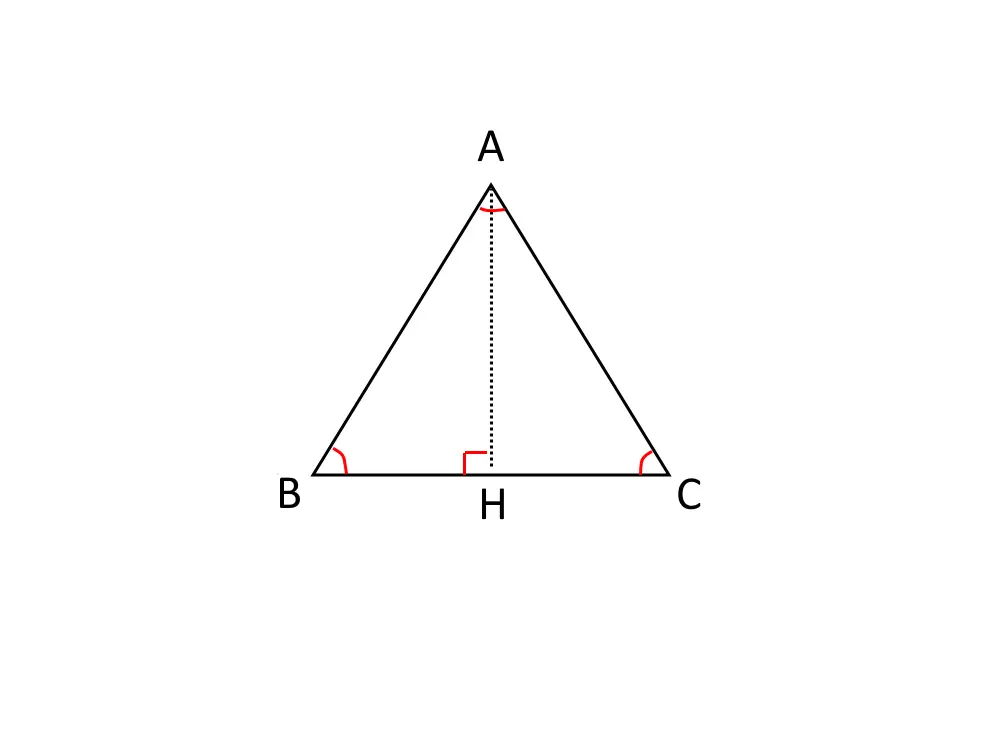
Ossia, tracciamo l’altezza del triangolo equilatero che taglia la base esattamente in due. I calcoli ed i ragionamenti sono esattamente gli stessi, quindi riportiamo la formula finale che abbiamo trovato:
\overline{AH} =\sqrt{ \overline{AB}^2 - (\frac{\overline{BC} }{2})^2 }
Per comodità chiamiamo con la lettera h l’altezza del triangolo equilatero, e con la lettera l il lato.
Quindi la formula la riscriviamo con le nuove lettere:
h =\sqrt{ l^2 - (\frac{l}{2})^2 }
Qui possiamo fare qualche calcolo in più ed ottenere una nuova formula. Svolgiamo il quadrato nella parentesi tonda:
h =\sqrt{ l^2 - \frac{l^2}{2^2} }
h =\sqrt{ l^2 - \frac{l^2}{4} }
All’interno della radice facciamo un minimo comune multiplo:
h =\sqrt{ \frac{4l^2 - l^2}{4} }
h =\sqrt{ \frac{3l^2 }{4} }
Il termine l^2 ed il 4 possiamo anche portarli fuori dalla radice, perchè sono dei quadrati. Otteniamo quindi una nuova formula che lega l’altezza ed il lato di un triangolo equilatero:
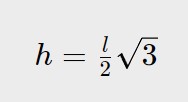
Vediamo adesso alcuni come usare le formule viste e problemi svolti utilizzando il Teorema di Pitagora!
Problemi Teorema di Pitagora
Problema 1. In un triangolo rettangolo ABC calcolare la lunghezza dell’ipotenusa \overline{AB} sapendo che gli altri due cateti misurano 3 cm e 4 cm.
Nei problemi di questo tipo la PRIMA cosa da fare è fare il disegno: importantissimo per non sbagliare formule e segni!
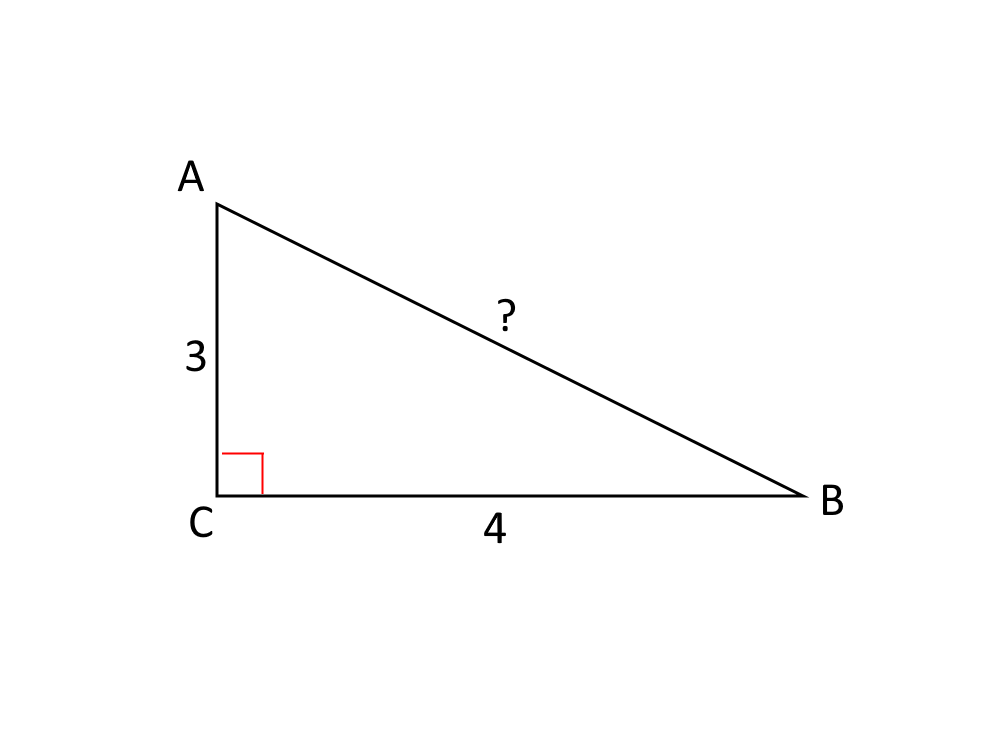
Questo è un triangolo rettangolo e quindi possiamo utilizzare il Teorema di Pitagora. Il problema ci chiede l’ipotenusa, e quindi usiamo la formula per calcolare l’ipotenusa.
i=\sqrt{C^2 + c^2}
Sostituiamo le lettere di questo problema però.
\overline{AB}=\sqrt{\overline{BC}^2 + \overline{AC}^2}
Sostituiamo i dati che il problema ci ha dato:
\overline{AB}=\sqrt{3^2 + 4^2}
\overline{AB}=\sqrt{9 + 16}
Otteniamo:
\overline{AB}=\sqrt{25} = 5\;cm
Ed abbiamo risolto il problema!
Problema 2. In un triangolo rettangolo ABC conosciamo l’ipotenusa \overline{AB} che misura 5 cm e il cateto minore che misura 3 cm. Quanto vale il cateto maggiore di questo triangolo?
Iniziamo a disegnare il triangolo e ciò che ci manca e che vogliamo calcolare.
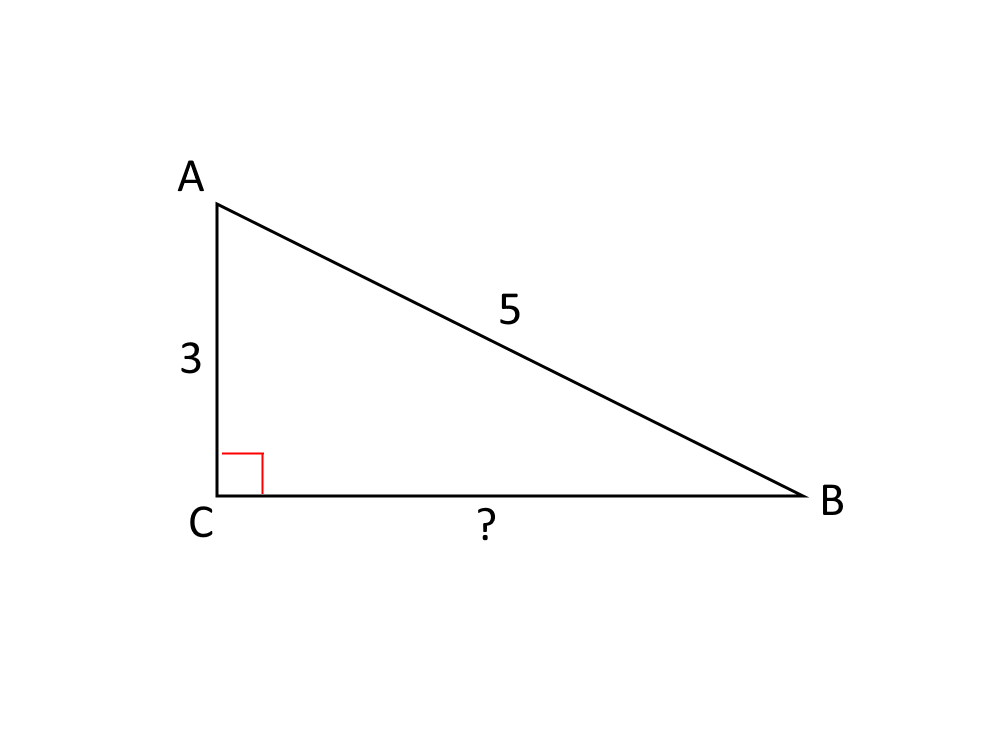
Abbiamo un triangolo rettangolo e quindi possiamo usare il Teorema di Pitagora. Il problema ci chiede la misura del cateto maggiore, quindi usiamo la formula seguente:
C=\sqrt{i^2 - c^2}
Sostituiamo però le lettere del nostro caso:
\overline{BC}=\sqrt{\overline{AB}^2 - \overline{AC}^2}
Sostituiamo nella formula i dati che il problema ci ha dato:
\overline{BC}=\sqrt{5^2 - 3^2}
\overline{BC}=\sqrt{25 - 9}
Otteniamo quindi che il cateto maggiore misura:
\overline{BC}=\sqrt{16} = 4 \; cm
Problema 3. In un triangolo isoscele conosciamo la base \overline{BC} che misura 6 cm e il lato che misura 5 cm. Calcolare l’altezza \overline{AH} del triangolo isoscele.
Iniziamo a disegnare il triangolo isoscele, dove ricordiamo che i due lati sopra la base sono uguali.
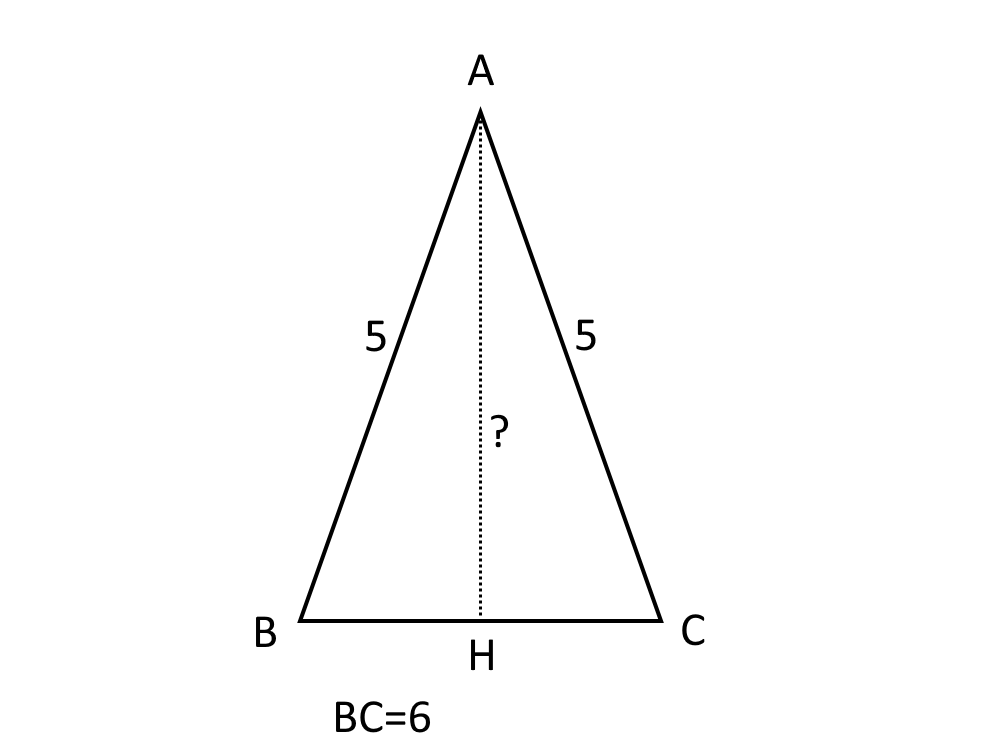
Il problema ci chiede l’altezza di un triangolo isoscele. Nel capitolo del Teorema di Pitagora: triangolo isoscele abbiamo calcolato utilizzando il Teorema di Pitagora l’altezza del triangolo isoscele, arrivando alla formula:
\overline{AH} =\sqrt{ \overline{AB}^2 - (\frac{\overline{BC} }{2})^2 }
Questa formula ci permette di calcolare l’altezza, conoscendo la base e il lato, quindi è perfetta per noi. Sostituiamo i dati che il problema ci ha dato:
\overline{AH} =\sqrt{ 5^2 - (\frac{6}{2})^2 }
\overline{AH} =\sqrt{ 5^2 - 3^2 }
Ricaviamo:
\overline{AH} =\sqrt{ 25 - 9 }
\overline{AH} =\sqrt{16 } = 4 cm
Problema 4. In un triangolo isoscele conosciamo l’altezza \overline{AH} che misura 12 cm, e il lato che misura 13 cm. Calcolare la base \overline{BC} del triangolo isoscele.
Facciamo il disegno, questo esercizio non è immediato.
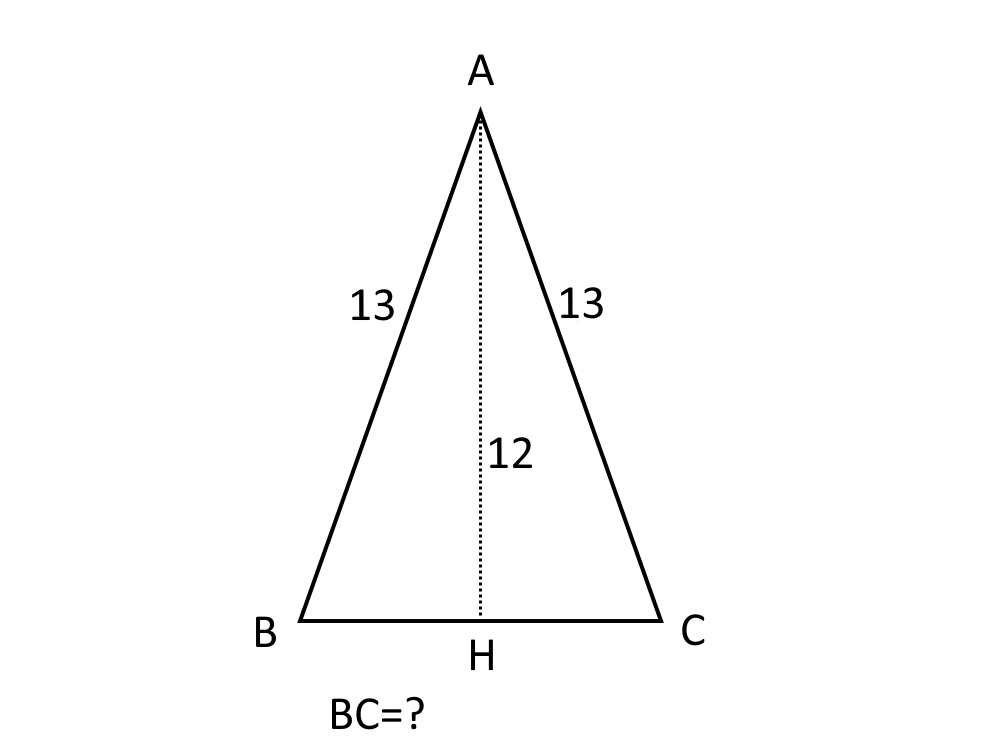
L’esercizio ci chiede un qualcosa per la quale non abbiamo una vera e propria formula precisa da utilizzare. Quindi in questi casi quello che vi consiglio sempre è di partire dal Teorema di Pitagora base. Quindi prendiamo il triangolo rettangolo ABH per la quale sappiamo che:
\overline{AB}^2=\overline{AH}^2 + \overline{BH}^2
Noi però vogliamo la base. La base, come vedete dal disegno, è:
\overline{BC}=2 \cdotp \overline{BH}
Quindi se calcoliamo \overline{BH} conosceremo tramite quest’ultima relazione anche la base. Quindi dobbiamo calcolarci \overline{BH} partendo dal Teorema di Pitagora prima scritto. Portiamo a primo membro \overline{BH} :
- \overline{BH}^2 + \overline{AB}^2=\overline{AH}^2
Portiamo \overline{AB}^2 a secondo membro:
- \overline{BH}^2 =-\overline{AB}^2 + \overline{AH}^2
Cambiamo tutto di segno perché ci fa comodo il primo termine positivo.
\overline{BH}^2 =\overline{AB}^2 - \overline{AH}^2
Ed ora possiamo applicare la radice quadrata ad ambo i membri, e calcolare finalmente questo \overline{BH} .
\overline{BH} =\sqrt{\overline{AB}^2 - \overline{AH}^2 }
Sostituiamo i dati che il problema ci ha dato:
\overline{BH} =\sqrt{13^2 - 12^2 }
\overline{BH} =\sqrt{169-144 }
Ossia:
\overline{BH} =\sqrt{25} = 5 \; cm
L’esercizio attenzione perché non è concluso! Il problema ci chiede \overline{BC} . Come detto prima sappiamo che:
\overline{BC}=2 \cdotp \overline{BH}
\overline{BC}=2 \cdotp 5 \; cm = 10\; cm
Problema 5. In un triangolo equilatero l’altezza misura 20 cm. Calcolare il perimetro del triangolo.
Il problema ci chiede il perimetro (ossia la somma dei lati). Quindi come prima cosa dobbiamo calcolare il lato, che in un triangolo equilatero sono uguali. Per quanto riguarda il triangolo equilatero la formula è una sola ed utilizziamo quindi questa:
h =\frac{l}{2} \sqrt{3}
Noi però abbiamo già l’altezza e vogliamo il lato, quindi dobbiamo isolare da una parte l. Moltiplichiamo tutto per 2:
2h =l \sqrt{3}
Adesso dividiamo per \sqrt{3} ed otteniamo così:
\frac{2h}{ \sqrt{3} } =l
Che essendo una uguaglianza significa che sinistra=destra e destra=sinistra. In parole povere è corretto scrivere i membri invertiti:
l = \frac{2h}{ \sqrt{3} }
A questo punto sostituiamo i dati forniti dal problema, ossia solo quello dell’altezza:
l = \frac{2\cdotp 20}{ \sqrt{3} } =23,1\;cm
Il perimetro significa somma dei lati, e visto che in un triangolo equilatero i lati sono tutti uguali allora:
2p= 23,1+23,1+23,1 =23,1 \cdotp 3 = 69,3\; cm
La pagina sul Teorema di Pitagora: formula e dimostrazione è conclusa! Abbiamo visto insieme anche come risolvere dei problemi usando il Teorema di Pitagora.
Trovate altre centinaia di esercizi svolti anche di altri argomenti sia di matematica che altro ancora! Continuate ad esercitarvi sul nostro sito!
Per approfondire:
https://it.wikipedia.org/wiki/Teorema_di_Pitagora