Equazioni spurie: FORMULE ed ESERCIZI SVOLTI con soluzioni
Le equazioni spurie: formule ed esercizi svolti! Seguite questa pagina con calma, prendetevi un tè e capirete tutto sulle equazioni spurie. Partiremo dalla definizione, ossia che cosa è una equazione spuria. Poi passeremo a mostrarvi le formule, e solo allora vi faremo vedere degli esercizi svolti, spiegati passo dopo passo. Capirete tutto senza problemi, non abbiate fretta però! In questa pagina c’è tutto ciò di cui avete bisogno per capire qualsiasi cosa sulle equazioni spurie. Alla fine mostreremo anche che il suo grafico è una parabola! Iniziamo subito.
Indice
- Che cosa è una equazione spuria: definizione
- Come si risolvono le equazioni spurie: formule
- ESERCIZI SVOLTI
- Equazioni spurie con frazioni
- Equazioni spurie con radici
- Come graficare la parabola di una equazione spuria
Detto questo, iniziamo subito a vedere cosa è una equazione spuria.
Che cosa è una equazione spuria: definizione
Andiamo con calma, passo dopo passo. Abbiamo studiato che cosa sono le equazioni di secondo grazo, e abbiamo visto che esse sono della forma seguente:
ax^2 +bx +c = 0
E fino a qui ci siamo no? Bene, le equazioni spurie sono un caso particolare di queste equazioni di secondo grado. Semplicemente esse hanno la stessa forma, ma gli manca il coefficiente “c”! Quindi nelle equazioni spurie c=0!
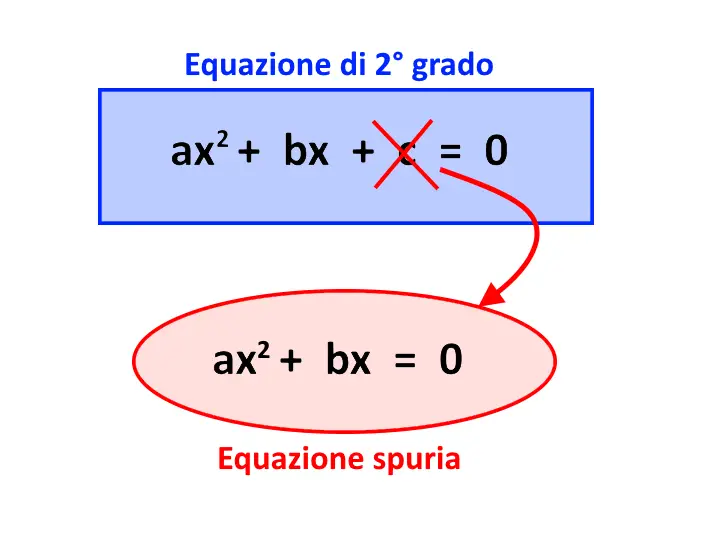
Ma quindi stiamo dicendo che le equazioni spurie non sono equazioni di secondo grado? Assolutamente no. Facciamo chiarezza su questo punto, poiché spesso solleva diversi dubbi.
Allora, partiamo da una cosa alla volta. Una equazione si dice di secondo grado se contiene il termine x^2 . Deduciamo allora che anche le equazioni spurie sono di secondo grado!
E allora quale è la differenza? Semplicemente che:
ax^2 +bx +c = 0 è una equazione di secondo grado, che possiamo definire “completa”, ossia che ha tutti e tre i coefficienti (a,b,c).
Mentre ax^2 +bx = 0 è una equazione di secondo grado, però “incompleta”, che chiamiamo equazione spuria.
Chiara la differenza? Ora che abbiamo capito cosa sono, passiamo a vedere il paragrafo successivo. Come le risolviamo a questo punto?
Come si risolvono le equazioni spurie: FORMULE
Abbiamo quindi capito che le equazioni spurie sono della seguente forma:
ax^2 +bx = 0
Ok, ma come le risolviamo? Una volta individuate, ci sono due formule da seguire per giungere alla soluzione. Prima di presentarvele, vi devo dire una cosa: non serve impararle a memoria! Nell’esempio di dopo vi farò vedere che non serve imparare a memoria queste due formule!
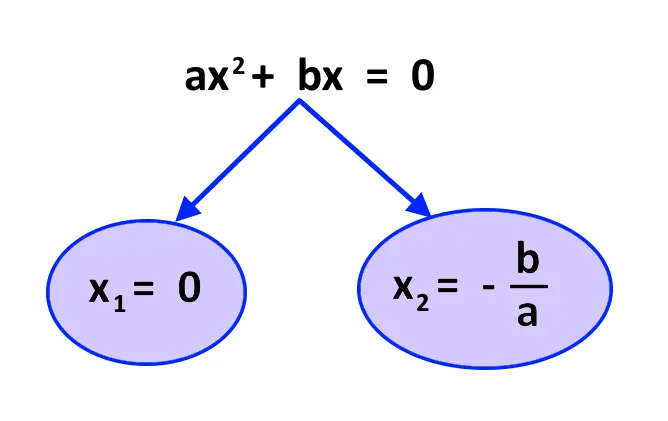
Quindi queste due formule ci condurranno alle soluzioni del libro. Però è inutile ricordarsele. Fidatevi di noi: è molto più semplice seguire l’esempio di sotto!
Esempio. 3x^2 + 2x = 0
Innanzitutto ci dobbiamo porre una domanda, quando arriveremo alla verifica in classe: questa qui è una equazione spuria? La risposta è sì poiché è della forma seguente, come abbiamo detto:
ax^2 +bx = 0
A questo punto fidatevi: evitate di usare quelle due formule! Se perdete il foglietto con le formule o non ve le ricordate come fate? E’ semplice, seguiteci.
Notiamo che possiamo sempre mettere in evidenza la x, nelle equazioni spurie (perché è presente la x in entrambi i termini), quindi:
x \cdotp (3x + 2) = 0
A questo punto come andiamo avanti? Notiamo che compare un prodotto fra due termini. Tale prodotto deve fare 0. Sappiamo che qualsiasi numero moltiplicato per 0 dà come risultato 0. Quindi almeno uno dei due deve fare 0! Ed è proprio questa la soluzione!
Partiamo infatti dal porre il primo termine (x) uguale a zero!
x=0
Questa è la prima soluzione x_1=0! Notiamo che è comparsa la prima formula!
E poi passiamo adesso al porre l’altro termine pari a zero! (quindi poniamo uno alla volta i due termini uguali a zero). Quindi:
(3x + 2) = 0
3x + 2 = 0
Isoliamo la x a sinistra, poiché vogliamo calcolare la x, quindi portiamo il -2 a destra.
3x = -2
Dividiamo tutto per 3 ed i giochi son fatti:
x = - \frac{2}{3}
Eccoci con la seconda soluzione! Notiamo che è proprio uguale alla seconda formula:
x_2 = - \frac{b}{a}=- \frac{2}{3}
Serve quindi imparare a memoria quelle due formule? Assolutamente no, e per di più lo svolgimento è sempre lo stesso. Quindi siate furbi! Quindi, ricapitolando otteniamo il seguente schema.

Ora che abbiamo capito come svolgere le equazioni spurie, passiamo a farvi vedere tantissimi esercizi svolti e spiegati, alcuni dei quali conterranno delle insidie, che vi faremo vedere come superare!
ESERCIZI SVOLTI sulle equazioni spurie
Esercizio 1. 7x^2 + 56x = 0
Quindi, da ora in poi, come detto in precedenza, andremo avanti senza mai usare a memoria quelle due formule. Facciamoci furbi che sono pochissimi passaggi! Come sempre, mettiamo in evidenza la x:
x(7x + 56) = 0
La prima soluzione sarebbe porre il primo termine (x) pari a zero, quindi:
x_1 = 0
Quando si giunge alla soluzione mettiamoci anche il “1” per fare capire che è la prima soluzione delle due.
Poi, poniamo il secondo termine pari a zero:
7x + 56 = 0
Isoliamo sempre la x a sinistra:
7x = -56
x = - \frac{56}{7}
L’esercizio è concluso, solamente che notiamo che quella frazione possiamo anche semplificarla! Provando a fare 56:7 alla calcolatrice, notiamo che ci dà il numero esatto (sezna virgola) 8. Di conseguenza la soluzione è più precisamente:
x_2 = - 8
Esercizio 2. -2x^2 + 2x = 0
E qui cosa dite, è una equazione spuria?
ax^2 +bx = 0
Per chi non avesse una risposta sicura, è importante che legga queste righe. Il coefficiente “a” è un numero, ma non deve per forza essere positivo (2,3,5,8,11…), ma può anche essere negativo (in questo caso abbiamo -2), e comunque rimane una equazione spuria! Questo discorso vale anche per il coefficiente “b”, e per qualsiasi altro coefficiente incontrerete in matematica, quindi tenete a mente queste parole!
E allora agiamo sempre seguendo il procedimento classico! Mettiamo prima di tutto in evidenza la x:
x(-2x + 2) = 0
La prima soluzione sarebbe il primo termine nullo, quindi:
x_1 = 0
L’altra come sempre:
-2x +2 = 0
-2x = -2
Cambiamo tutto di segno:
2x = 2
E poi dividiamo per 2:
x_2 = 1
L’esercizio è concluso. Alcuni di voi si staranno chiedendo: ma scusami io mi sono accorto che potevo mettere in evidenza anche il 2, quindi lo posso fare oppure no?
Certo che sì! Il risultato non cambia! Anzi, sarebbe stato ancora più comodo. Di fatti mettendo in evidenza il 2x:
2x(-x + 1) = 0
Il primo termine si deve annullare quindi:
2x = 0 \implies x = 0
E ci ritroviamo la stessa prima soluzione di prima. Se non vi è chiaro questo passaggio, pensate che dovete trovare una x che moltiplicata per 2, dia zero. Se moltiplico 2 per 0 darà 0, e quindi la x soluzione è 0!
L’altra invece:
-x + 1 = 0 \implies x= 1
Possiamo in generale mettere in evidenza quello che notiamo si possa mettere, ma deve sempre contenere la x, non dimenticatevela!
Esercizio 3. x^2 = 2x
Questa ha una forma un po’ diversa da quella che noi dobbiamo avere. Noi vogliamo ricondurci a:
ax^2 +bx = 0
Però, nulla da preoccuparsi, portiamo semplicemente il 2x a primo membro (ricordandoci sempre che si cambia segno quando si passa da una parte all’altra):
x^2 - 2x = 0
Adesso sì che ci torna familiare! Mettiamo in evidenza, e seguiamo lo stesso procedimento dell’esercizio precedente:
x(x - 2) = 0
La prima soluzione è x_1 = 0
L’altra è invece:
x - 2 = 0 \implies x =2
E quindi x_2 = 2
Esercizio 4. t^2 - 4t = 0
Notiamo fin da subito una cosa: qui abbiamo la lettera “t” invece della solita x, e come si fa? Beh, la variabile può essere chiamata come si vuole. Di conseguenza qualsiasi lettera troviate, il procedimento non cambia. Semplicemente qui ricaveremo le soluzioni t_1, t_2 ! Agiamo come sappiamo fare:
t(t - 4) = 0
La prima è t_1 = 0
La seconda è:
t - 4 = 0
t_2 = 4
Quindi non preoccupatevi quando trovate una lettera diversa dalla x, è sempre uguale il procedimento!
Esercizio 5. (x-3)(x+3) = 2x-9
Qui abbiamo una forma complicatuccia. Dobbiamo quindi prima svolgere alcuni calcoli. L’obiettivo di questi calcoli è sempre lo stesso: semplificare l’equazione! Dobbiamo levare allora le parentesi.
Per chi non se lo ricorda, questo è il caso di usare la formula della differenza dei quadrati.
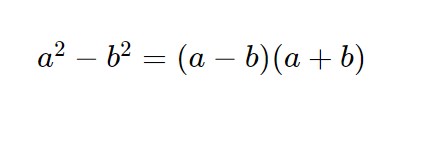
Vediamo la formula al contrario chiaramente. Avremo:
x^2 -9 = 2x-9
Non ci sono più parentesi, abbiamo fatto il nostro. Portiamo tutto al primo membro per vedere se si tratta di una equazione spuria:
x^2 -9 - 2x+9 =0
x^2 - 2x =0
Eh sì, lo è! Da ora in poi sapete come svolgere l’esercizio, provateci voi e poi rivenite qui!
x(x - 2) =0
La prima è x=0
L’altra è x=2.
Esercizio 6. (t+2)^2 - (2-t)^2 = t^2
Questa sembra davvero difficile…da cosa iniziamo? Notiamo fin da subito che abbiamo dei quadrati da svolgere. Iniziamo proprio da quelli. Il nostro obiettivo quando le cose non sono semplici è: levare le parentesi che ci sono. Dobbiamo alla fine ricondurci alla forma di una classica equazione spuria.
Usiamo la formula del quadrato del binomio.
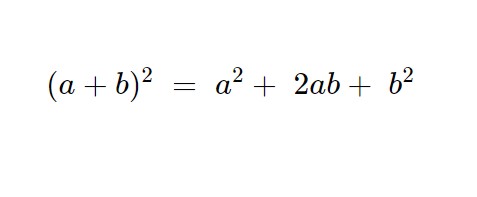
Ricordiamo però di lasciare le parentesi, quelle le leviamo dopo!
(t^2 + 4 + 4t) - (4 + t^2 -4t ) = t^2
Le leviamo solo adesso! Questo perché nel secondo caso abbiamo un segno meno davanti, e questo ci può far non trovare con la soluzione. Il segno meno davanti ad una parentesi vuol dire che dobbiamo cambiare il segno a tutti i termini dentro la parentesi. Quindi:
t^2 + 4 + 4t - 4 - t^2 + 4t = t^2
Se ancora avete dubbi su questo passaggio: non dovete cambiare il segno solo al primo termine (il 4), ma a tutti e tre!
Abbiamo il termine t^2 - t^2 che leviamo. Poi abbiamo anche 4-4 e leviamo anche questo.
+ 4t + 4t = t^2
Sommiamo i primi due:
8t = t^2
Portiamo tutto a primo membro, e ci siamo ricondotti alla forma di una equazione spuria finalmente!
- t^2 +8t =0
Ora possiamo iniziare a seguire il solito procedimento per la risoluzione, che abbiamo fatto negli scorsi esercizi. Quindi mettiamo in evidenza la t:
t(- t +8) =0
Deduciamo che t_1 = 0
L’altra è:
-t+8 = 0
-t = -8
Cambiamo di segno tutto:
t_2 = 8
Ed eccoci finalmente alla fine di questo esercizio.
Esercizio 7. (2x+3)^3 = 8x^3 +27
Qui notiamo che salta all’occhio la presenza di un termine x^3. La professoressa non è pazza, se esce un termine di questo tipo sappiate che si leverà facendo i conti! Anzi, si deve levare, altrimenti non sapremmo risolverla. Quindi il fatto che si cancellerà questo termine ci darà un indizio che stiamo facendo bene i conti.
Svogliamo il cubo del binomio, sfruttando la seguente formuletta.
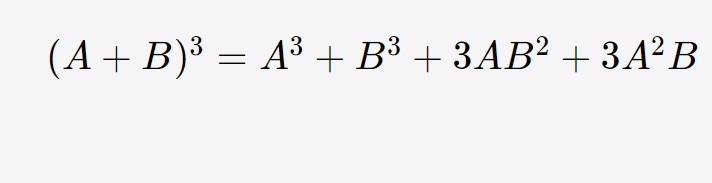
Avremo:
8x^3 + 27 + 3(2x)^2 \cdotp 3 +3(2x) \cdotp 9 = 8x^3 +27
Leviamo queste fastidiose parentesi, svolgendo le moltiplicazioni e le potenze.
8x^3 + 27 + 36x^2 + 54x = 8x^3 +27
Portiamo tutto a primo membro:
8x^3 + 27 + 36x^2 + 54x - 8x^3 -27 =0
Ed ecco un segno che stiamo facendo bene: il termine cubico se ne va! (Anche il 27 se ne va)
36x^2 + 54x =0
Siamo tornati alla nostra familiare equazione spuria.
x(36x + 54) =0
\implies x_1 = 0
36x + 54 =0 \implies x_2 = - \frac{54}{36} = - \frac{3}{2}
Vediamo ora come comportarci quando ci sono le frazioni.
Equazioni spurie con frazioni
In questo paragrafo vedremo alcuni esercizi svolti di equazioni spurie, con presenza di frazioni. Sarà dunque necessario fare spesso il minimo comune multiplo. Vediamoli!
Esercizio 1. \frac{a^2 + a}{3} = 8a^2 - \frac{7a}{2}
La logica generale per la risoluzione non cambia all’inizio: bisogna sempre portare tutto a primo membro e cercare di ricondurci alla solita forma che ormai conosciamo bene:
ax^2 +bx = 0
E allora come facciamo se ci sono delle frazioni? La prima cosa da fare è comunque portare tutto a sinistra.
\frac{a^2 + a}{3} - 8a^2 + \frac{7a}{2} = 0
Poi non si va avanti se non facciamo il minimo comune multiplo. Arrivati a questo punto è un must! Il denominatore sarà 6 (3 per 2)
\frac{a^2 + a}{3} - 8a^2 + \frac{7a}{2} = 0
\frac{2a^2 + 2a -48a^2 + 21a }{6} = 0
Se non sapete fare il minimo comune multiplo, vi invito prima ad impararlo, e poi rivenite qui. Comunque, fatto ciò possiamo moltiplicare tutto per 6, e quindi sbarazzarci della frazione!
\frac{2a^2 + 2a -48a^2 + 21a }{6} \cdotp 6 = 0 \cdotp 6
2a^2 + 2a -48a^2 + 21a = 0
Sommiamo i termini simili (sommiamo i due termini quadratici, e poi sommiamo i due termini con la “a”):
-46a^2 + 23a = 0
E siamo arrivati alla forma che conosciamo. Da questo punto in poi sapete cosa fare.
a(-46a + 23) = 0
a_1 = 0
E poi -46a + 23 = 0 \implies a_2 = \frac{23}{46} = \frac{1}{2}
Esercizio 2. ( \frac{1}{2} + \frac{1}{4} x )^2 = ( \frac{3}{2} x + 1 ) \frac{1}{4}
Prima di fare ogni altra cosa, compare un bel quadrato da risolvere. Partiamo da quello!
( \frac{1}{4} + \frac{1}{16} x^2 + 2\frac{1}{2} \frac{1}{4}x ) = ( \frac{3}{2} x + 1 ) \frac{1}{4}
\frac{1}{4} + \frac{1}{16} x^2 + \frac{1}{4}x = ( \frac{3}{2} x + 1 ) \frac{1}{4}
Il primo membro è apposto, libero da parentesi tonde. Passiamo al secondo in cui dobbiamo solo svolgere una moltiplicazione.
\frac{1}{4} + \frac{1}{16} x^2 + \frac{1}{4}x = \frac{3}{8} x + \frac{1}{4}
Fatto ciò, come prima (imparate il procedimento, è sempre lo stesso), portiamo tutto a sinistra:
\frac{1}{4} + \frac{1}{16} x^2 + \frac{1}{4}x - \frac{3}{8} x - \frac{1}{4} =0
Ora è il turno del minimo comune multiplo, ma prima di partire a razzo, osserviamo l’equazione: abbiamo una frazione che se ne va!
\frac{1}{16} x^2 + \frac{1}{4}x - \frac{3}{8} x =0
Ora sì che possiamo andare a fare l’mcm!
\frac{x^2 +4x - 6x }{16} =0
Moltiplicando per 16, leviamo la linea frazionaria.
x^2 +4x - 6x =0
x^2 - 2x =0
Eccoci in una cosa più umana. Sappiamo come agire.
x(x - 2) =0
x_1 = 0, x_2 = 2
Esercizio 3. - \frac{ x(x-4) }{6} + \frac{x+4}{3} \cdotp \frac{2-x}{2} - \frac{4}{3} =0
Questa è davvero difficile. E’ segnata come massima difficoltà sul libro, quindi concentrati! Abbiamo già tutto a primo membro, questo è vero. C’è da svolgere prima una moltiplicazione fra le due frazioni. Se non vi ricordate come si fanno, basti sapere che bisogna moltiplicare i denominatori fra di loro, e poi i numeratori fra di loro. Otteniamo:
- \frac{ x(x-4) }{6} + \frac{ (x+4)(2-x) }{6} - \frac{4}{3} =0
Sciogliamo anche queste parentesi, facendo la moltiplicazione fra loro due. Facciamo lo stesso anche per il primo termine.
- \frac{ x^2 - 4x }{6} + \frac{ 2x-x^2 +8 -4x }{6} - \frac{4}{3} =0
Non c’è più nulla da fare, passiamo al minimo comune multiplo!
\frac{ -(x^2 - 4x) + 2x-x^2 +8 -4x - 8 }{6} =0
Notate che il segno meno non ce lo siamo dimenticati. Esso è applicato a tutta la prima frazione! Leviamo il 6.
-(x^2 - 4x) + 2x-x^2 +8 -4x - 8 =0
Ricordatevi che si cambia il segno a tutti i termini contenuti all’interno.
-x^2 + 4x + 2x-x^2 +8 -4x - 8 =0
Sommiamo ciò che possiamo sommare:
-2x^2 + 2x =0
E risolviamola ora!
x(-2x + 2) =0
x_1 = 0
x_2 = 1
E se ci sono delle radici come facciamo?
Equazioni spurie con radici
Le equazioni spurie non sembrano essere così difficili, ma potrebbero rappresentarsi un problema quando ci sono di mezzo le radici e non ci si ricorda le proprietà di esse. Quindi è utile che facciate insieme a noi questi pochi esercizi sulle radici, così riprendete la mano!
Esercizio 1. 2 \sqrt{2} x^2 - \frac{3}{4} x = 0
Partiamo da un esercizio base. Abbiamo già la forma di una equazione spuria classica:
ax^2 +bx = 0
I coefficienti sembrano strani, con radici e frazioni, ma effettivamente ci sono a e b:
a = 2 \sqrt{2}
b = - \frac{3}{4}
E allora agiamo fin da subito come sappiamo fare. Questo esercizio è utile perché vi ricorderemo una proprietà delle radici che serve spesso, negli esercizi con le radici.
x( 2 \sqrt{2} x - \frac{3}{4} ) = 0
\implies x_1 = 0
L’altro termine poi dobbiamo porlo pari a zero:
2 \sqrt{2} x - \frac{3}{4} = 0
2 \sqrt{2} x = \frac{3}{4}
Otteniamo:
x = \frac{3}{ 4 \cdotp 2 \sqrt{2} }
L’esercizio sembra finito, eppure non ci troviamo con la soluzione del libro. Come mai? La risposta è che si preferisce avere la radice sempre al numeratore, quindi bisogna razionalizzare.
Ricordiamo che la razionalizzazione consiste nel moltiplicare e dividere per la radice, in modo tale da portare la radice sopra.
Quindi moltiplichiamo e dividiamo per la radice che abbiamo:
x = \frac{3}{ 8 \sqrt{2} } \frac{\sqrt{2} }{\sqrt{2} }
Queste sono cose che uno può averle dimenticate, e noi siamo qui per voi. Al denominatore abbiamo:
\sqrt{2} \cdotp \sqrt{2} = ( \sqrt{2})^2 = 2
Quindi giù la radice se ne va, e rimane solo sopra. Ecco quindi completato il processo di razionalizzazione, ossia di portare la radice sopra:
x = \frac{3 \sqrt{2} }{ 16 }
Esercizio 2. a^2 + \sqrt{5} a = \sqrt{2} a
Come detto già in altri simili esercizi, la lettera diversa non ci deve far spaventare. L’incognita la possiamo chiamare x come anche a o con altre lettere, non cambia nulla.
Portiamo a primo membro tutto:
a^2 + \sqrt{5} a - \sqrt{2} a = 0
Mettiamo in evidenza la a, poiché vogliamo la a preceduta da un solo coefficiente.
a^2 + ( \sqrt{5} - \sqrt{2} )a = 0
Notate come ci siamo ricondotti a:
ax^2 +bx = 0
Dove ora il coefficiente b è:
b = \sqrt{5} - \sqrt{2}
Questa può essere una cosa nuova per molti, ma se ci pensate b è sempre un numero solo. Alla fine se provate a fare alla calcolatrice quella sottrazione vi verrà un solo numero, ossia un solo coefficiente.
Fatto ciò mettiamo in evidenza la a a tutta l’equazione spuria:
a(a + ( \sqrt{5} - \sqrt{2}) ) = 0
a(a + \sqrt{5} - \sqrt{2} ) = 0
La prima soluzione è a=0. L’altra la si ricava ponendo nulla la quantità:
a + \sqrt{5} - \sqrt{2} = 0
Portiamo le radici a destra, ed i giochi son conclusi:
a = - \sqrt{5} + \sqrt{2}
Esercizio 3. 3x^2 = x ( 6 + \sqrt{3} x )
Portiamo a primo membro:
3x^2 - x ( 6 + \sqrt{3} x ) = 0
Questa NON è una forma di una equazione spuria! C’è da stare attenti qui. Per chi non lo avesse notato, se ci facessimo andare bene questo, allora avremmo:
b = 6 + \sqrt{3} x
Esso contiene al suo interno una x, e quindi b non è un numero puro. Non è quindi un coefficiente. Non va bene. E allora svolgiamo la moltiplicazione con la parentesi tonda:
3x^2 = 6x + \sqrt{3} x^2
3x^2 - 6x - \sqrt{3} x^2 =0
Raccogliamo insieme il termine quadratico, un po’ simile a ciò che abbiamo fatto nell’esercizio di prima:
( 3- \sqrt{3} ) x^2 - 6x =0
Ed eccoci qui in una equazione spuria. Ora il coefficiente a:
a= 3- \sqrt{3}
Risolviamola!
x[( 3- \sqrt{3} )x - 6] =0
x_1 = 0
Poi l’altra non è semplicissima da risolvere ed è:
( 3- \sqrt{3} )x - 6=0
Bisogna molto stare attenti alle parentesi, quindi fate con calma questi piccoli passaggi. Isoliamo la x:
( 3- \sqrt{3} )x = 6
x = \frac{6}{ 3- \sqrt{3} }
Proprio come abbiamo detto nel primo esercizio, non ci va bene tenere una radice al denominatore (infatti non vi troverete col libro), e allora razionalizziamo. Quando c’è qualcos’altro al denominatore, oltre la radice, come faccio a razionalizzare?
La risposta è: bisogna moltiplicare e dividere per il denominatore, cambiato del segno centrale:
x = \frac{6}{ 3- \sqrt{3} } \frac{ 3+ \sqrt{3} }{ 3+ \sqrt{3} }
Perché questo? Perché così possiamo sfruttare la differenza dei quadrati, nel prodotto fra i denominatori.
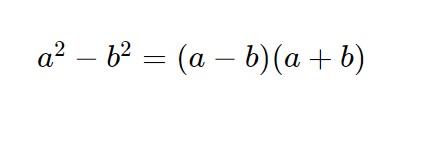
Nel nostro caso, applicando al denominatore questa formula (letta chiaramente al contrario):
x = \frac{6(3+ \sqrt{3}) }{ 3^2 - \sqrt{3}^2 }
x = \frac{ 18 + 6\sqrt{3} }{ 9 - 3 }
x = \frac{ 18 + 6\sqrt{3} }{ 6 }
Sopra possiamo mettere in evidenza il 6:
x = \frac{ 6(3 + \sqrt{3}) }{ 6 }
E semplificare:
x = 3 + \sqrt{3}
Esercizio 4. 2 \sqrt{7} +( x-2 )( \sqrt{7} + x ) = 0
Qui non c’è da porsi domande: abbiamo una moltiplicazione da fare per levare le parentesi, facciamola. Seguite con il dito le moltiplicazioni con i vari termini per non dimenticarvene nessuno. Sta di fatto che alla fine vi devono venire 4 termini.
2 \sqrt{7} + \sqrt{7}x + x^2 - 2 \sqrt{7} -2x = 0
Leviamo di torno quel termine che va via:
\sqrt{7}x + x^2 -2x = 0
Mettiamo in evidenza la x per raccogliere, e far comparire il coefficiente unico b:
x^2 + ( \sqrt{7} -2 )x = 0
Abbiamo l’equazione spuria classica. Iniziamo col solito:
x(x + \sqrt{7} -2 ) = 0
x_1 = 0
Poi la seconda:
x + \sqrt{7} -2 = 0
x = - \sqrt{7} +2 = 0
Esercizio 5. ( \sqrt{2} x + \sqrt{3} )( \sqrt{3}x - \sqrt{2} ) = - \sqrt{6}
Svolgiamo subito il prodotto fra parentesi tonde! Scriviamo tutti i termini esplicitamente, senza fare cose a mente, poiché potremmo sbagliare non essendo semplice.
\sqrt{2} \sqrt{3} x^2 - \sqrt{2} \sqrt{2} x + \sqrt{3} \sqrt{3} x - \sqrt{2} \sqrt{3} = - \sqrt{6}
Analizziamo ciò che abbiamo. Notiamo che, abbiamo per due volte:
\sqrt{3} \sqrt{3} = 3
\sqrt{2} \sqrt{2} = 2
Apportiamo le modifiche nel frattempo:
\sqrt{2} \sqrt{3} x^2 - 2x +3x - \sqrt{2} \sqrt{3} = - \sqrt{6}
Poi, ricordiamo una proprietà delle radici fondamentale per concludere l’esercizio. Ossia:
\sqrt{2} \sqrt{3} = \sqrt{2 \cdotp 3} = \sqrt{6}
E quindi:
\sqrt{6} x^2 - 2x +3x - \sqrt{6} = - \sqrt{6}
Portando tutto a primo membro, grazie a questa proprietà appena usata, possiamo levare un termine.
\sqrt{6} x^2 - 2x +3x - \sqrt{6} + \sqrt{6} = 0
\sqrt{6}x^2 + x = 0
Mettiamo in evidenza la x e finiamo.
x(\sqrt{6}x + 1) = 0
x_1 = 0
\sqrt{6}x + 1 = 0
Ciò implica la seconda soluzione:
x = - \frac{1}{ \sqrt{6} }
Razionalizziamo:
x = - \frac{1}{ \sqrt{6} } \frac{\sqrt{6}}{ \sqrt{6} } = - \frac{\sqrt{6}}{ 6 }
Come ultimo paragrafo vediamo come si ottiene il grafico, passatemi il termine, di una “funzione spuria”.
Come graficare la parabola di una equazione spuria
L’obiettivo di questo paragrafo è ottenere il grafico di una funzione “spuria”. Consideriamo la seguente funzione spuria:
y = 2x^2 +4x
Essendo il grafico di una funzione abbiamo bisogno di aggiungere la y a sinistra, e levare il “=0”.
Vedendo nella pagina sulla parabola, notiamo che questo è il caso della “parabola con asse parallelo ad y“. Ossia quello con equazione:
y = ax^2 +bx +c = 0
Però con il coefficiente c=0.
Per ottenere il grafico abbiamo dunque bisogno di:
- Disegnare il vertice
- Segnare diversi punti della funzione
Il fuoco e la direttrice non sono necessari per il grafico di questa equazione: calcolateli solo se vi viene chiesto dalla professoressa. Se volete ottenere solo un semplice grafico allora vi servono quelle due cose scritte nell’elenco di sopra.
Per il fuoco la formuletta da usare è:
F=(- \frac{b}{2a}, \frac{1- \Delta }{4a} )
Abbiamo tutto tranne il delta, calcoliamolo:
\Delta = b^2 - 4ac = 4^2 - 4 \cdotp 2 \cdotp 0 = 16
Il fuoco è dunque il punto seguente, che andiamo anche a segnare sul piano cartesiano.
F=(- \frac{4}{4}, \frac{1- 16 }{8} ) = (- 1, - \frac{15 }{8} )
Abbiamo segnato il fuoco. Adesso ci manca solo da trovare alcuni punti del grafico, scegliamo delle x casuali, e calcoliamo la y corrispondente. Come la calcoliamo la y dopo aver scelto una x qualsiasi? Se avete scelto come x=2, vi basta andare a sostituire nella funzione:
y = 2(2)^2 +4 \cdotp 2 = 16
Facciamo una tabella con dei punti, il più vicino possibile a -1 (ascisse del fuoco), questo è un consiglio.
| x | y |
| -2 | 0 |
| -3 | 6 |
| 0 | 0 |
| 1 | 6 |
Segniamo questi punti sul grafico, e uniamo il tutto. Il grafico che ne risulta è la seguente parabola di questa equazione spuria.
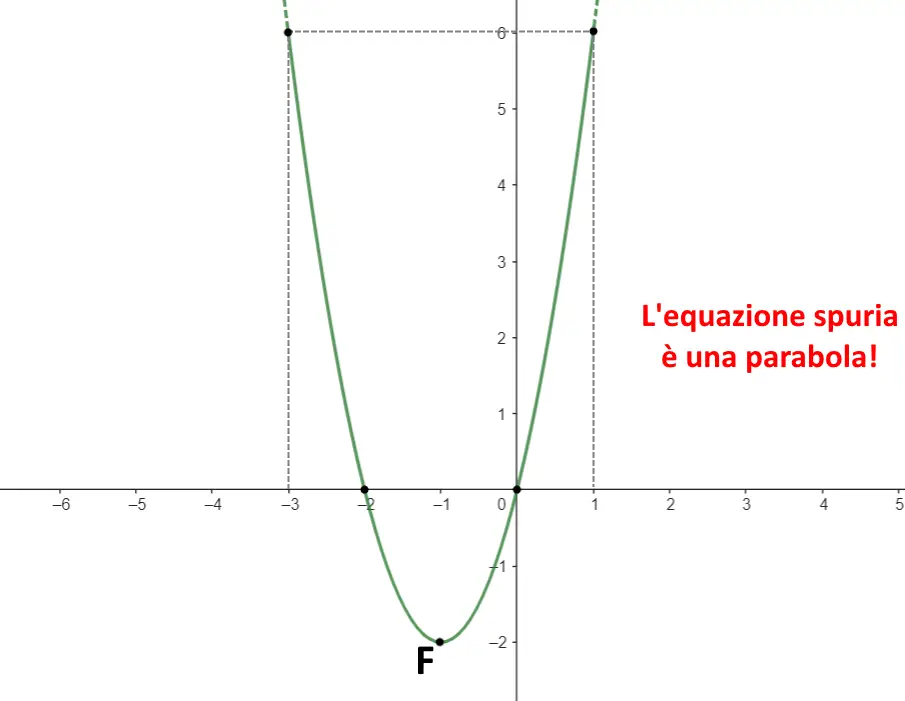
In questa pagina abbiamo davvero sviscerato tutto riguardo le equazioni spurie, non c’è più altro da aggiungere. Se però avete dubbi o vorreste alcuni approfondimenti fatecelo sapere per email!