Riesci a collegare i due VERTICI di un CUBO?

Oggi vediamo per la prima volta in questo sito (bellissimo sito), un test logico-matematico divertentissimo, senza utilizzo di calcoli, ma con ragionamento volto ad un poco di Geometria ed intuizione! Adatto a tutti.

E’ un Test non banale, e lo potete fare ai vostri amici appassionati di Logica, li sorprenderete! Ed allora iniziamo a vedere la traccia di questo Test.

TRACCIA: Abbiamo un cubo, di lato di lunghezza qualsiasi. Abbiamo due vertici A e B, opposti nel cubo. Opposti significa che non fanno parte della stessa superficie (per capirci), ma sono collegati dalla diagonale interna.

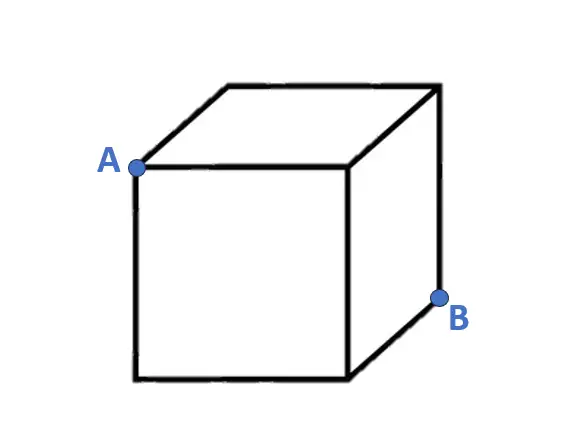
La domanda di questo Test è: qual è il percorso più breve sulla superficie, per arrivare da A a B?

Quindi ricapitolando dovete unire A e B con una linea sopra la superficie del cubo, come questa seguente (che serve da esempio di come dovete fare). Ovviamente non potete quindi passare per dentro al cubo, altrimenti sarebbe troppo banale!

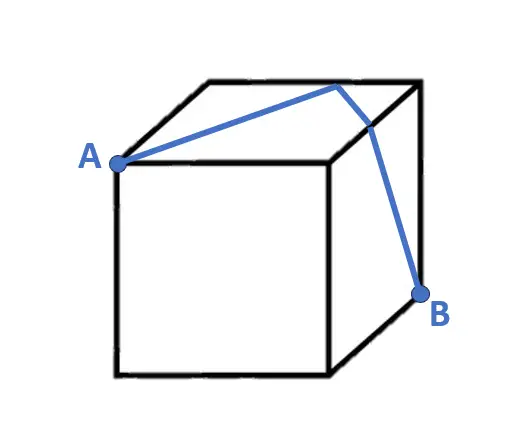
Prendete carta e penna, provateci, divertitevi e passate del tempo con la bellissima Logica! Nella sezione successiva vedremo la soluzione.

Soluzione: percorso più breve per unire A e B

Quello che possiamo notare, come cosa preliminare, è che fra A e B ci sono due superfici che li separano. E’ chiaro che si potrebbe pensare a percorsi che passino per tre superfici o quattro, o anche di più: ma non avrebbe senso! Ricordiamoci che ci stiamo chiedendo quale è il percorso più piccolo. Quindi ci basiamo sul trovare un percorso che passa per due superfici.

Per comodità di spiegazione, andiamo a rappresentare allora A e B in modo bidimensionale. Questo ci servirà per capire meglio, e rendere tutto più intuitivo. Ovviamente alla fine ritorneremo alla rappresentazione cubica.

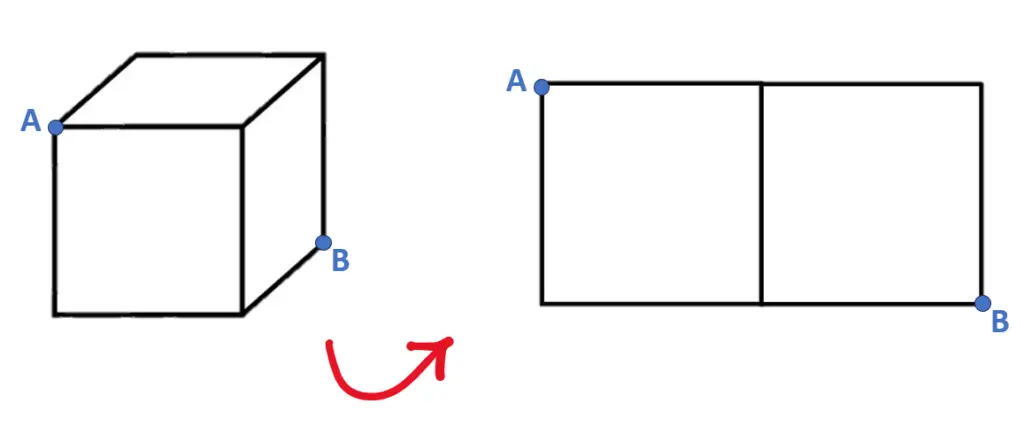
A questo punto, se ci domandiamo il percorso più breve per unire A e B, la risposta è ovvia. E’ semplicemente una linea dritta che li unisce, quindi la diagonale del rettangolone per capirci.

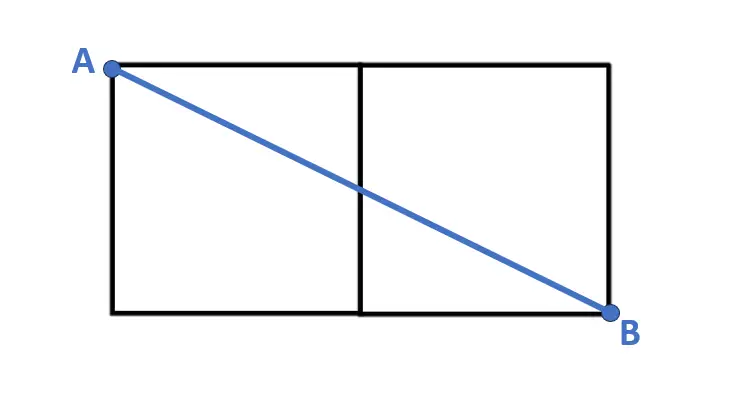
E’ chiaro che non possiamo avere certezza matematica che poi questo percorso sarà il più breve, ritornando nella rappresentazione cubica. Ma notiamo una cosa importantissima.

Partiamo da questo percorso che abbiamo disegnato, come punto di partenza. Se uniamo A e B con altri percorsi, qualsiasi altro percorso, si verrà a creare un triangolo. Questo triangolo ha come ipotenusa AB, il percorso disegnato in partenza.

Ma noi sappiamo, da un po’ di Geometria, che la somma dei cateti di un triangolo è sempre maggiore della lunghezza dell’ipotenusa. Quindi stiamo dicendo che l’ipotenusa è sempre il percorso più piccolo, rispetto a percorrere la lunghezza di due cateti.

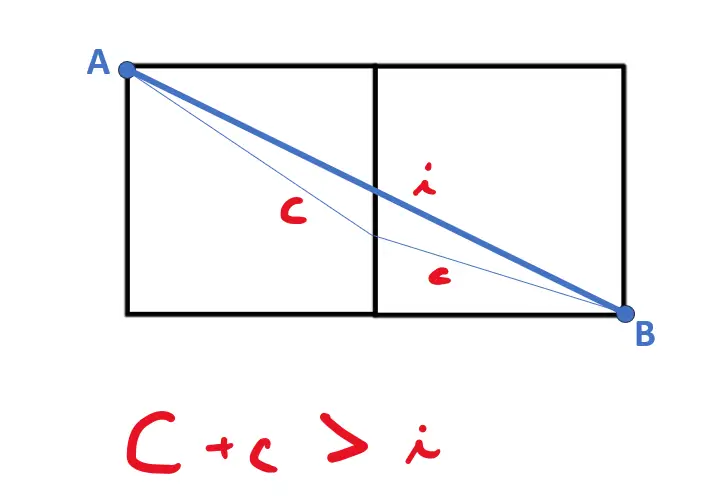
Ricordiamo che questo non è un caso particolare, questo è ciò che succede scegliendo qualsiasi altro percorso che non sia AB.

Ora che abbiamo capito che questo, in rappresentazione bidimensionale, rappresenta il percorso ovviamente più breve, dobbiamo ritornare al cubo. E come si fa?

Beh, notiamo che tale percorso passa per il punto centrale del lato di mezzo del rettangolone. Quindi useremo questo come sistema di riferimento, e ci troveremo quindi un percorso sul cubo, del tipo seguente.

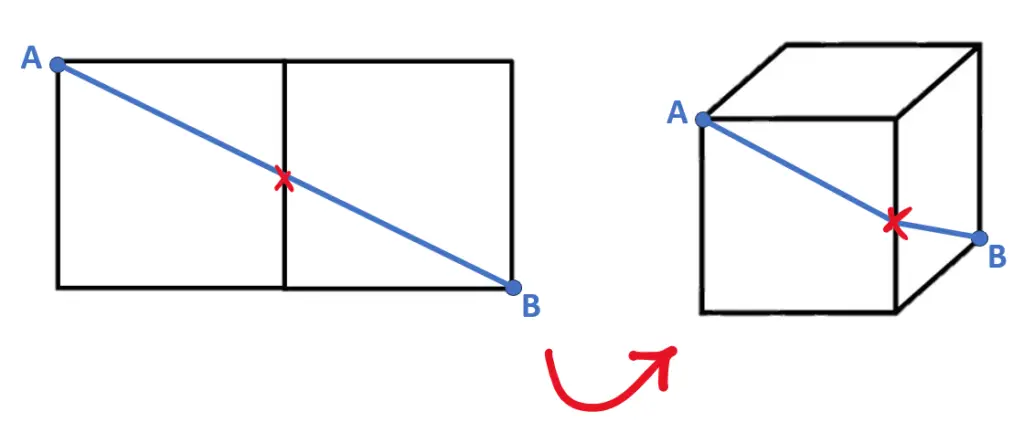
Quindi il percorso più breve quale è? E’ quello che parte da A, con una linea dritta arriva alla metà del lato verticale del cubo, e poi arriva a B.

E’ chiaro che, essendoci simmetria, possiamo anche far passare il percorso sulla superficie di sopra, e poi scendere fino a B: anche questa è una medesima soluzione.

Speriamo che questo Test, improntato più sulla Geometria questa volta, vi sia piaciuto. Nel caso ne avreste altri fatecelo sapere per email!