ESPRESSIONI con POTENZE: 15 esercizi SVOLTI e spiegati!
In questa pagina vedremo ben 15 esercizi svolti e spiegati in ogni singolo passaggio, per quanto riguarda le “espressioni con potenze”. In questa pagina ci sarà tutto, quindi non avrete bisogno di cliccare dieci volte in diverse pagine!
Partiamo con il ripetere efficacemente le proprietà delle potenze (le useremo negli esercizi!), e poi applicheremo queste regole negli esercizi risolti.
Indice
Cominciamo quindi, prendetevi un foglio e una penna e farete gli esercizi insieme a noi!
Proprietà delle potenze
Durante gli esercizi useremo (sempre) tutte queste proprietà, che vi mostreremo facili da memorizzare, quindi segnatele da parte su qualche foglio, poiché le richiameremo!
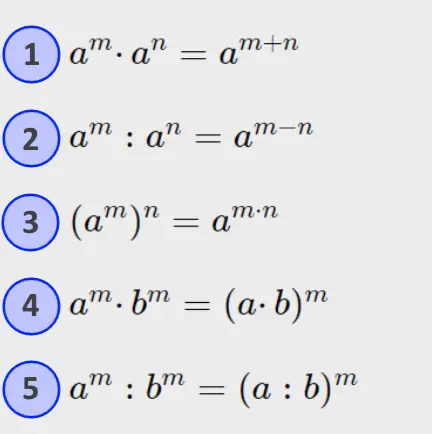
Detto questo, partiamo con l’applicazione di queste proprietà nelle “espressioni con le potenze”.
Espressioni con potenze
Cominciamo con gli esercizi, fidatevi se vi diciamo che ognuna di queste espressioni vi farà capire cose diverse e sempre più in profondità. Il nostro intento è farvi capire, non imparare a memoria le cose, poiché ci si confonde e non va bene!
Semplifica le seguenti espressioni.
Esercizio 1. 6^4 : 6^2 : 3^2
Partiamo dal presupposto che ci sono più modi per risolvere una espressione, tutti equivalenti. L’importante è trovarsi col libro.
La prima regola che vale sempre in matematica è: osservare la traccia, per pensare ad una strategia, prima di iniziare a scrivere cose a caso e meccanicamente.
Allora, notiamo che abbiamo due divisioni da fare. La regoletta è che si risolvono le divisioni in ordine, quindi a partire da sinistra.
Quindi il primo passaggio sarà svolgere il termine:
6^4 : 6^2
Ricordando le proprietà delle potenze, che vi abbiamo elencato all’inizio della pagina, questo che caso è? E’ chiaramente l’uso della proprietà numero 2! Abbiamo infatti una stessa base (cioè il 6, il numero che sta a “terra”) e poi abbiamo una divisione. Seguendo la proprietà, essa ci dice che il risultato ci darà lo stesso numero di base (6) ma con esponente che è dato dalla sottrazione degli esponenti (4-2):
6^4 : 6^2 = 6^{4-2} = 6^2
Mettiamo questo primo pezzo nell’espressione dell’esercizio!
6^2 : 3^2
Ci rimane questo…possiamo fare ancora qualcos’altro? Assolutamente sì. Prima di vedere l’elenco delle proprietà, cosa notiamo? Beh, notiamo che l’esponente è uguale! Ecco che siamo alla proprietà 5!
Il risultato ci darà un numero che ha come esponente sempre 2, ma come base (6:3) la divisione delle basi. Queste proprietà dopo qualche esercizio vi verranno naturali, non preoccupatevi! Quindi:
6^2 : 3^2 =(6:3)^2
Sapendo che 6:3 fa 2, allora otteniamo:
2^2
Una volta arrivati ad una potenza, abbiamo finito di fare calcoli. Ora dobbiamo solo scrivere il risultato per esteso (cioè un numero senza potenze). Ricordiamo qui la definizione di potenza.
2^2 = 2 \cdotp 2 = 4
4 è la soluzione dell’esercizio!
Esercizio 2. (-3)^4 \cdotp (-3)^3 : (-3)^6
Come detto prima, non partiamo a razzo. Vediamo cosa notiamo, così ci facciamo una idea del risultato e di cosa dobbiamo fare. Le basi sono tutte uguali, quindi sfrutteremo le proprietà 1 e 2 ovviamente!
Partiamo da sinistra, abbiamo prima di tutto un prodotto:
(-3)^4 \cdotp (-3)^3
Usando la proprietà 1, ne consegue che:
(-3)^4 \cdotp (-3)^3 = (-3)^{4+3} = (-3)^7
Non lasciatevi spaventare dalla base negativa, essa è pur sempre un numero! Un consiglio per ricordarvi le proprietà è che quando c’è di mezzo la moltiplicazione allora dovremo sommare gli esponenti. Se invece abbiamo una divisione, dovremo sottrarre gli esponenti.
Sostituiamo nell’espressione il primo pezzetto ottenuto:
(-3)^7 : (-3)^6
Basi uguali, passiamo alla proprietà sorella di quella appena usata!
(-3)^7 : (-3)^6 = (-3)^{7-6} = (-3)^1
Ci è venuto:
(-3)^1
Ed ora? Beh, ricordiamo una cosa fondamentale. Se eleviamo un numero alla 1, ci viene il numero di base e basta (per es. 5^1 = 5 ). Quindi possiamo lasciare solo la base:
-3
Non c’è più nulla da fare, abbiamo ottenuto un numero solo, va bene così: esercizio svolto!
Esercizio 3. (-5)^2 : (-5)^0 \cdotp (-5)^3 : (-5)^4
Qui abbiamo già quattro pezzetti, separati da operazioni. Quello “0” ci fa spaventare, ma ora lo affronteremo senza temere. Partiamo sempre da sinistra, e pensiamo proprio a questo pezzo che ci fa dubitare:
(-5)^2 : (-5)^0
Cerchiamo di distogliere lo sguardo dallo zero, cosa abbiamo? Basi uguali? Benissimo, allora usiamo senza pensarci la proprietà 2 sempre.
(-5)^{2-0} = (-5)^2
Tutto qui, non c’era da spaventarsi! Lo zero è un numero, e si comporta come gli altri.
Ci rimane ora:
(-5)^2 \cdotp (-5)^3 : (-5)^4
Possiamo fare un passaggio alla volta, oppure usare una piccola scorciatoia! Abbiamo basi uguali no? Quindi applicando la proprietà solita, dovremmo sommare o sottrarre gli esponenti, vero? Si sommano gli esponenti quando c’è la moltiplicazione. Si sottraggono gli esponenti quando c’è la divisione. Piuttosto che fare ogni volta un passaggio (ci mettiamo 30 anni), facciamo tutto in una volta.

Stessa base, ricordiamoci la regoletta sugli esponenti:
(-5)^{ 2+3-4 } = (-5)^{1} = -5
In questo esercizio abbiamo imparato un comodissimo trucchetto!
Esercizio 4. [ 4^4 \cdotp (-3)^4 ]^2 : (-2)^8
Vediamo un’altra cosa nuova in questo esercizio: la presenza della parentesi quadra. Per affrontarla è semplice. Basta solo sapere che si devono risolvere prima le parentesi tonde all’interno di essa, e poi alla fine la parentesi quadra.
Ricapitolando, pensiamo prima a ciò che sta dentro, risolvendolo:
4^4 \cdotp (-3)^4
Cosa notiamo? Adesso notiamo stesso esponente, di conseguenza verrà fuori:
( 4 \cdotp -3)^4 = (?)^4
Cosa viene dal prodotto fra 4 e -3? Se avete la possibilità, usate la calcolatrice. Altrimenti, basta moltiplicare semplicemente i numeri, e quindi viene 12. Poi per il segno, abbiamo un + e poi un -: sapendo che “+ per – fa -“, verrà -12.
( 4 \cdotp -3)^4 = (-12)^4
Mettiamolo dentro alla parentesi quadra:
[ (-12)^4 ]^2 : (-2)^8
Abbiamo una potenza, elevata ad un’altra potenza (potenza dentro la parentesi quadra, il tutto elevato al quadrato), quindi sfrutteremo per la prima volta la proprietà 3!
Essa ci dice che dobbiamo rimanere la stessa base, e scrivere la moltiplicazione fra gli esponenti:
[ (-12)^4 ]^2 = (-12)^{4 \cdotp 2} = (-12)^8
Completiamo l’espressione, inserendoci questo pezzo:
(-12)^8 : (-2)^8
Lo sappiamo fare? Sì, provatelo a fare da soli, poi tornate qui!
(-12: -2)^8
La divisione avrà come numero 12:2 = 6, e poi come segno la regola dei segni “- diviso per – fa +”.
(6)^8
Questo numerone è troppo grande, quindi decidiamo di lasciarlo così, va bene lo stesso.
Esercizio 5. [ (7^3)^4 : 7^5] : [ 7^7 : 7^2 ]
Osserviamo l’espressione con le potenze: abbiamo due parentesi quadre che si dividono. Quindi il focus main è quello di risolvere prima il valore dentro le parentesi quadre.
Come detto, prima però si devono risolvere le parentesi tonde che compaiono. In questo caso abbiamo solo il termine:
(7^3)^4
Questo rientra nella proprietà 3, ossia “potenza di potenza”. Basta moltiplicare gli esponenti:
(7^3)^4 = 7^ {3 \cdotp 4} = 7^{12}
Sostituiamo nell’espressione, che ora avrà solo parentesi quadre.
[ 7^{12} : 7^5] : [ 7^7 : 7^2 ]
Ora tocca alle quadre! Svolgiamo in maniera separata, i conti nelle due parentesi, poiché per ora non hanno niente a che fare fra di loro, dentro.
[ 7^{12-5} ] : [ 7^{7-2} ]
[ 7^{7} ] : [ 7^{5} ]
Una volta che non ci sono conti da fare, possiamo anche levare le parentesi.
7^{7} : 7^{5}
7^{7-5} = 7^2
Esso da’ 49.
Esercizio 6. 9^2 : 3^3
Questo esercizio è UTILISSIMO. Vi servirà tante volte. Qui non abbiamo né basi uguali né esponenti uguali, non possiamo usare nessuna proprietà, cosa facciamo?
In questi casi bisogna “manipolare” una delle due basi (di solito sempre la più grande, quindi il 9). L’obiettivo è scrivere il 9, come un numero che ha come base un 3, così avremo stessa base.
Di fatti sappiamo che 9 = 3 \cdotp 3 = 3^2
Scriviamo quindi il 9 così:
(3^2)^2 : 3^3
Ricordate che l’esponente non c’entra nulla, stiamo sostituendo solo il 9. L’esponente poi rimane perché sono due cose diverse, fate attenzione!
Partiamo allora da sinistra, risolvendo quella “potenza di potenza”.
3^{2 \cdotp 2} : 3^3
3^4 : 3^3
Grazie a questi passaggi, siamo arrivati ad una espressione di potenze che sappiamo benissimo risolvere, fatelo voi!
3^{4-3 } = 3^1 = 3
Esercizio 7. 6^5 : (-6)^2
Questa espressione è come prima, ossia non c’è niente di uguale (anche le basi sono diverse perché a sinistra abbiamo 6 e poi -6). Però qui c’è qualche differenza: la base è la stessa, tranne per quel segno meno.
L’obiettivo di questo esercizio sarà di manipolare quel segno meno per levarlo da mezzo, ed avere così stessa basi.
Analizziamo il termine (-6)^2 .
Vediamo quanto fa:
(-6)^2 = -6 \cdotp -6 = 36
Notiamo che, essendo elevato per un numero pari, il segno meno diventa più. Quindi il risultato è proprio lo stesso di fare:
(6)^2 = 6 \cdotp 6 = 36
Ed allora, essendo la stessa cosa, scriviamolo senza il segno meno. Questo lo si può fare anche sfruttando la proprietà 4. Di fatti, pensando al – come “-1”:
(-6)^2 = (-1 \cdotp 6 )^2 = (-1)^2 \cdotp 6^2 = 6^2 = 36
L’espressione dell’esercizio diventa dunque risolvibile adesso con un passaggio!
6^5 : 6^2
6^{5-2} = 6^3
Esercizio 8. (343)^4 : (-49)^2
Anche questo esercizio è davvero molto esemplare, poiché questo è un diverso caso di esercizio visto fino ad ora. MondoFisica vi propone solo esercizi utilissimi!
Qui abbiamo basi diverse ed esponenti diversi. Sugli esponenti non possiamo farci nulla, quindi dove agiamo? Sulle basi sicuramente. Se possiamo fare qualcosa, quel qualcosa è alle basi sicuro.
Abbiamo dei numeri strani, quindi prendiamo in mano la calcolatrice. Partiamo dal “49”: iniziamolo a dividere per dei numeri sulla calcolatrice, fino a che non troviamo un suo divisore. Notiamo che facendo 49:7=7 ottimo! E’ un suo divisore! Facendo diviso 7 ancora fa 1, quindi possiamo scrivere:
49:7:7=1 \implies 7^2 = 49
Questo passaggio di sopra è un po’ come se fosse il “passaggio inverso” per trovare come scriverlo in base 7. In pratica, il 7 è la base, e poi quante volte ho fatto la divisione è l’esponente.
Provvediamo a sostituire nell’espressione:
(343)^4 : (-7^2)^2
Ricordando il discorso fatto prima, cioè che se ho un segno meno elevato al quadrato (o in generale elevato ad una potenza pari), allora esso darà +, quindi è equivalente non scriverlo proprio.
(343)^4 : (7^2)^2
Passiamo alla prima base. Anche in questo caso mano alla calcolatrice. Non partiamo a razzo dividendo per numeri a caso, notiamo una cosa importante: per usare la proprietà 2, necessariamente il primo termine dovrà avere anch’esso base 7, e allora proviamo a dividerlo per 7!
343:7:7:7=1 \implies 7^3 = 343
Ne segue che:
(7^3)^4 : (7^2)^2
Ora, abbiamo sia a sinistra che a destra una “potenza di potenza”, quindi risolviamo moltiplicando i rispettivi esponenti:
7^{3 \cdotp 4} : 7^{2 \cdotp 2}
7^{12} : 7^4
La soluzione dell’esercizio è:
7^{12-4} = 7^8
Ecco fatto!
Esercizio 9. (-8)^3 : (4)^2
ATTENZIONE: questo esercizio non è lo stesso di prima e contiene una cosa nuova! Questa espressione con potenze assomiglia alla precedente, ma contiene una difficoltà che non sapete ancora affrontare, ma che ora vi diremo!
Iniziamo sempre ad osservare ciò che abbiamo avanti: esponenti e basi diverse. Quindi? Sempre cercare di rendere stesse basi, poiché non possiamo cambiare gli esponenti.
Il -8 sarà la difficoltà di questo particolare esercizio. Partiamo dunque dal 4 che è più semplice, e che sapete fare. Esso è facilmente dato da:
4:2:2=1 \implies 2^2 = 4
Sostituiamo semplicemente nella traccia:
(-8)^3 : (2^2)^2
Passiamo al focus di questo esercizio, quel -8. Perché è difficile se l’abbiamo visto in precedenza? Beh, è vero che possiamo scriverlo come:
8:2:2:2=1 \implies 2^3 = 8
E quindi:
(-2^3)^3 : (2^2)^2
Ma quel segno meno non possiamo levarlo!!! Come mai? Il segno meno lo possiamo levare se esso è elevato per una potenza pari (perché – per – fa +). Ma se abbiamo il segno meno per una potenza dispari come 3, allora esso darà “- x – x – = -“, rimane ancora!!!
E quindi come facciamo? Beh, ragioniamo su ciò che abbiamo di fronte. Abbiamo una divisione fra due numeri, e fino a qui ci siamo. Il primo numero è negativo (perché c’è il segno meno), ed il secondo numero sarà positivo ovviamente (perché non c’è nessun segno meno).
Ok, e allora? Fare la divisione fra un numero negativo per uno positivo darà…un numero negativo! Basta fare, per esempio, -4:2 = -2, vedete come esce fuori un numero col segno meno!
E allora? Fatto questo ragionamento, visto che il segno meno rimane, possiamo portare il segno meno davanti a tutto, rimanendolo fino alla fine.
- (2^3)^3 : (2^2)^2
Come vedete lo scriviamo proprio davanti, ce lo portiamo fino alla fine, e nel frattempo continuiamo a svolgere i calcoli.
Abbiamo due “potenze di potenze”:
- 2^{3 \cdotp 3} : 2^{2 \cdotp 2}
- 2^9 : 2^4
(In questi passaggi, per ciò che abbiamo detto all’inizio, non leviamo mai il segno meno)
- 2^{9 - 4 }
Che ci darà come risultato della semplificazione dell’espressione:
- 2^5
Ecco fatto! Abbiamo imparato una cosa nuova ancora!
Ora che abbiamo capito le applicazioni base, passiamo a esercizi più lunghetti, che potrebbero uscire nel compito in classe o all’esame di terza media!
Espressioni con le potenze difficili
Nel precedente paragrafo vi abbiamo fatto vedere gli esercizi base, in cui c’erano i concetti madre per capire le espressioni con le potenze. Adesso aumentiamo la difficoltà, sempre gradualmente però, quindi non spaventiamoci. Essi però saranno utili per la verifica in classe. Le spiegazioni saranno meno lunghe, poiché i passaggi principali i abbiamo già argomentati e discussi.
Esercizio 10. \{ - [4^3 \cdotp (-4)^3 ]^2 \} : (-8)^5 : (-2)
Partiamo con un esercizio, dove compare anche la parentesi graffa. La regoletta è la seguente: prima le tonde, poi le quadre ed infine le graffe. Questo discorso va fatto per le parentesi dentro la graffa. Nel senso che, non dobbiamo risolvere prima tutte le tonde (mi riferisco agli ultimi due termini), ma solo le tonde dentro la quadra. C’è una bella differenza, spero abbiate capito.
Quindi partiamo dall’unica tonda dentro la quadra. Per esso vale il discorso che, il segno meno non si può levare, e quindi lo portiamo davanti (questo lo abbiamo argomentato in uno degli esercizi precedenti a fondo, quindi rivedetelo).
\{ - [- 4^3 \cdotp (4)^3 ]^2 \} : (-8)^5 : (-2)
Abbiamo sia esponenti uguali che basi uguali per tale termine. In questo caso scegliete voi quale proprietà usare, è lo stesso! Noi per esempio scegliamo la 1.
\{ - [- 4^{3+3} ]^2 \} : (-8)^5 : (-2)
\{ - [- 4^6 ]^2 \} : (-8)^5 : (-2)
Passiamo alla quadra: essa è una “potenza di potenza”, in più abbiamo un segno meno elevato al quadrato, e che di conseguenza possiamo levare.
\{ - 4^{6 \cdotp 2} \} : (-8)^5 : (-2)
\{ - 4^{12} \} : (-8)^5 : (-2)
Ci rimane la graffa da svolgere, prima di passare alle altre tonde (ricordiamo che si parte da sinistra quando si ha a che fare con moltiplicazioni e divisioni). Per la graffa non dobbiamo fare nulla, quindi leviamola tranquillamente.
- 4^{12} : (-8)^5 : (-2)
Prima di cominciare con i calcoli, valutiamo i segni. Nel primo termine abbiamo un segno meno che non possiamo levare (poiché sta davanti al numero, e non è elevato a niente). Nel secondo termine non possiamo levarlo, quindi avanza un segno meno. Nel terzo termine non possiamo levarlo.
Dunque, avanzano tresegni meno!
-4^{12} : (-8)^5 : (-2)
Ricordando che “meno diviso meno fa più”, avanzerà un segno meno!
- 4^{12} : 8^5 : 2
Fatto il discorso dei segni (la cosa sempre più fastidiosa, che vi consigliamo di occuparvene il prima possibile), osserviamo l’espressione: basi diverse ed esponenti diverse.
Notiamo che possiamo portare tutto alla stessa base. Non vi faremo vedere come si fa, poiché già l’abbiamo discusso in 3-4 esercizi precedenti. Il risultato è:
- (2^2)^{12} : (2^3)^5 : 2^1
Potenza di potenza:
- 2^{2 \cdotp 12} : 2^{3 \cdotp 5} : 2^1
-2^{24} : 2^{15} : 2^1
Abbiamo divisione di tre basi uguali, facciamo il passaggio in una volta (è una comodissima scorciatoia, che vi invito sempre ad usare, piuttosto che fare tanti passaggi ed aumentare le possibilità di sbagliare):
-2^{24-15-1} = - 2^8
Esercizio 11. (-5^6) : [-25^2 : (-5^3)]^3 \cdotp (-1)^{13} - (-7^3)^2 : (-49)^2
Consiglio prima di iniziare: nella verifica in classe comparirà una espressione con potenze simili a questa, molto lunga. Prima di fare qualsiasi cosa, iniziamo a levare di mezzo la quadra, poi penseremo al resto.
Lì dentro, c’è il termine -25^2 cui non si può fare niente per il segno meno, poiché esso non è elevato a niente, ma sta semplicemente davanti alla potenza, che è diverso! Se invece avessimo avuto (-25)^2 allora sì che lo potevamo levare.
Nella tonda all’interno, si può portare davanti (esponente dispari):
(-5^6) : [-25^2 : - 5^3]^3 \cdotp (-1)^{13} - (-7^3)^2 : (-49)^2
“meno diviso meno fa più”:
(-5^6) : [25^2 : 5^3]^3 \cdotp (-1)^{13} - (-7^3)^2 : (-49)^2
Poi scriviamo con stessa base:
(-5^6) : [(5^2)^2 : 5^3]^3 \cdotp (-1)^{13} - (-7^3)^2 : (-49)^2
(-5^6) : [5^4 : 5^3]^3 \cdotp (-1)^{13} - (-7^3)^2 : (-49)^2
Di conseguenza:
(-5^6) : 5^3 \cdotp (-1)^{13} - (-7^3)^2 : (-49)^2
Ora pensiamo alle varie tonde che figurano. Come primo passaggio discutiamo sempre sui segni! Nel primo termine sta davanti (non possiamo fare niente). In (-1)^{13} = -1 . In (-7^3)^2 il segno è elevato alla potenza dispari, e così via…
Scriviamo il risultato di tale discussione sui segni:
-5^6 : 5^3 \cdotp (-1) - (7^3)^2 : (49)^2
Riguardo il primo pezzettone, c’è la moltiplicazione con un -1, che ci porta a:
5^6 : 5^3 - (7^3)^2 : (49)^2
Il segno meno che rimane riguarda una sottrazione, non c’entra niente con i discorsi fatti fino ad adesso. Anzi, non è possibile applicare le proprietà fra tutte le potenze, ma dobbiamo applicarle per i due pezzettoni in modo separato, come segue:
5^{6-3} - (7^3)^2 : (7^2)^2
5^3 - 7^6 : 7^4
Come vedete stiamo trattando il pezzo con base 5 e quello con base 7 in modo separatissimo, essi non interferiscono in nessun modo, poiché le proprietà delle potenze riguardano esclusivamente moltiplicazione e divisione.
5^3 - 7^2
125 - 49 = 76
Esercizio 12. [(-27)^4 : (9^2)^3]^{13} - \{ (-8)^3 : (-4)^4 + 81^2 : [2^0 + 2^5 : (2^2)^2 ]^7 \}
Questa è davvero molto lunga! Quando le espressioni con le potenze sono così lunghe, bisogna spezzettarla e pensare passo dopo passo, quindi una cosa alla volta. Pian piano si riesce a semplificarla. Notiamo che c’è una sottrazione che distacca un primo pezzo da un secondo pezzo. Possiamo pensare dunque di iniziare a concentrarci sul primo pezzo, che è anche il più breve. Al secondo poi ci penseremo.
Scriviamo con stessa base i due numeri che figurano:
[(-3^3)^4 : ((3^2)^2)^3]^{13} - \{ (-8)^3 : (-4)^4 + 81^2 : [2^0 + 2^5 : (2^2)^2 ]^7 \}
Nel secondo termine viene una “potenza di potenza” per due volte. Anche qui vale la scorciatoia per la quale scriviamo una sola moltiplicazione contenente tre numeri:
[(-3)^{3 \cdotp 4} : 3^{2 \cdotp 2 \cdotp 3} ]^{13} - \{ (-8)^3 : (-4)^4 + 81^2 : [2^0 + 2^5 : (2^2)^2 ]^7 \}
[(-3)^{12} : 3^{12} ]^{13} - \{ (-8)^3 : (-4)^4 + 81^2 : [2^0 + 2^5 : (2^2)^2 ]^7 \}
La divisione darà ovviamente 1: abbiamo che due numeri uguali si dividono (è come se ci fosse tipo 6:6=1) e quel segno meno se ne va perché elevato alla 12.
[1 ]^{13} - \{ (-8)^3 : (-4)^4 + 81^2 : [2^0 + 2^5 : (2^2)^2 ]^7 \}
1 elevato alla potenza pari ridà un 1, scriviamocelo:
1 - \{ (-8)^3 : (-4)^4 + 81^2 : [2^0 + 2^5 : (2^2)^2 ]^7 \}
Ecco quindi che abbiamo concluso il primo pezzo. Un primo gradino è stato salito, ora passiamo al secondo. Vedete, passo dopo passo, con calma anche le espressioni più lunghe risultano non impossibili.
Prima di pensare alle prime tonde…pensiamo alle tonde dentro la quadra. Sulla somma non si può far niente, dunque pensiamo alla divisione.
1 - \{ (-8)^3 : (-4)^4 + 81^2 : [2^0 + 2^5 : 2^{2 \cdotp 2} ]^7 \}
1 - \{ (-8)^3 : (-4)^4 + 81^2 : [2^0 + 2^5 : 2^4 ]^7 \}
Dunque:
1 - \{ (-8)^3 : (-4)^4 + 81^2 : [2^0 + 2^1 ]^7 \}
Sulla somma di potenze non si può agire, lo abbiamo detto tante volte. Chiaramente non possiamo fermarci qui. L’unica strada da percorrere è quella di scrivere esplicitamente il valore della somma (1+2). Di fatti ricordiamo che:
2^0 = 1, 2^1 = 2
1 - \{ (-8)^3 : (-4)^4 + 81^2 : 3^7 \}
Dentro la graffa, possiamo pensarla come due pezzi distaccati, come “primo pezzo + secondo pezzo”. Dunque pensiamoli in maniera differente. Scriviamo con stessa base entrambi:
1 - \{ (-2^3)^3 : (-2^2)^4 + (3^4)^2 : 3^7 \}
Consiglio: ci sono dei conti da fare, per non sbagliare pensiamo prima al segno che verrà. Il primo segno meno rimane poiché elevato ad una potenza dispari. Il secondo segno meno se ne va perché elevato ad una potenza pari (4), dunque lo leviamo.
1 - \{ (-2^3)^3 : (2^2)^4 + (3^4)^2 : 3^7 \}
Svolgiamo, usando la proprietà 3 prima:
1 - \{ -2^9 : 2^8 + 3^8 : 3^7 \}
Rimane da fare le divisioni, stiamo per giungere finalmente al termine ragazzi!
1 - \{ -2 + 3 \}
1 - \{ 1 \}
Il segno meno davanti ad una parentesi cambia di segno!
1-1=0
Finalmente finito! Se riuscite a fare questo esercizio, potete stare tranquilli per la verifica in classe!!!
Esercizio 13. [ - (256^3 : 32^3 )^2 ] : [ -2^{3^2} \cdotp (-2)^3 \cdotp (-2^2 )^2 ] \cdotp [ (15^4 : 5^4) \cdotp (-3^2) : 9^2 ]
Guardiamo in faccia questa espressione, ci salta all’occhio la struttura del tipo “primo pezzo : secondo pezzo x terzo pezzo”. L’esercizio si baserà sulla semplificazione di ogni singolo pezzo, uno per volta, concentrandoci all’inizio sul primo.
Partiamo dalla discussione del segno meno come sempre: esso si trova davanti alla parentesi tonda e non è elevato a nessuna potenza, lo lasciamo.
Nella tonda abbiamo stesso esponente, quindi applichiamo la rispettiva proprietà:
[ - ((256:32)^3)^2 ] : [ -2^{3^2} \cdotp (-2)^3 \cdotp (-2^2 )^2 ] \cdotp [ (15^4 : 5^4) \cdotp (-3^2) : 9^2 ]
L’elevazione al quadrato riguarda proprio tutto, per questo abbiamo messo un’altra parentesi tonda, per non confonderci.
[ - (8^3)^2 ] : [ -2^{3^2} \cdotp (-2)^3 \cdotp (-2^2 )^2 ] \cdotp [ (15^4 : 5^4) \cdotp (-3^2) : 9^2 ]
Abbiamo come risultato del primo pezzo il seguente termine:
[ -8^6 ] : [ -2^{3^2} \cdotp (-2)^3 \cdotp (-2^2 )^2 ] \cdotp [ (15^4 : 5^4) \cdotp (-3^2) : 9^2 ]
Passiamo al secondo pezzettone. Volendo, possiamo anche levare la prima quadra in tutto questo. Ancora, andiamo a discutere riguardo i segni. Il primo meno non ci si può far niente, il secondo meno è elevato alla terza dunque lo lasciamo fuori, l’ultimo invece è elevato alla seconda e lo leviamo.
-8^6 : [ -2^{3^2} \cdotp -2^3 \cdotp (2^2 )^2 ] \cdotp [ (15^4 : 5^4) \cdotp (-3^2) : 9^2 ]
Due segni meno che si moltiplicano daranno “+”, quindi li leviamo tutti.
-8^6 : [ 2^{3^2} \cdotp 2^3 \cdotp (2^2 )^2 ] \cdotp [ (15^4 : 5^4) \cdotp (-3^2) : 9^2 ]
Qui si hanno già tutti 2 come base. Analizziamo da parte il termine seguente che non abbiamo mai visto:
2^{3^2}
Come si fa? Cosa è? Partiamo da ciò che vediamo: è sicuramente una potenza, essa ha 2 come base. All’esponente si dovrà avere un numero, quale è? Esso é 3^2 = 9, dunque più facilmente possiamo scriverlo meglio:
-8^6 : [ 2^9 \cdotp 2^3 \cdotp (2^2 )^2 ] \cdotp [ (15^4 : 5^4) \cdotp (-3^2) : 9^2 ]
Partiamo dalla proprietà più complicata, ossia la 3. Scriviamo le potenze di potenze prima di tutto:
-8^6 : [ 2^9 \cdotp 2^3 \cdotp 2^4 ] \cdotp [ (15^4 : 5^4) \cdotp (-3^2) : 9^2 ]
Usiamo la “scorciatoia” per fare la doppia moltiplicazione in una botta:
-8^6 : [ 2^{9+3+4 } ] \cdotp [ (15^4 : 5^4) \cdotp (-3^2) : 9^2 ]
Anche il secondo è andato!
-8^6 : 2^{16} \cdotp [ (15^4 : 5^4) \cdotp (-3^2) : 9^2 ]
Ci rimane il terzo da completare e analizzare. Partiamo come sempre dai segni, quell’unico meno non è elevato a niente (solo il 3 è elevato alla seconda), dunque lo portiamo fuori a tutto. Passiamo poi alla prima parentesi tonda:
-8^6 : 2^{16} \cdotp - [ 3^4 \cdotp (3^2) : 9^2 ]
Scriviamo il 9 meglio, così abbiamo tutte basi uguali!
-8^6 : 2^{16} \cdotp - [ 3^4 \cdotp (3^2) : 3^4 ]
-8^6 : 2^{16} \cdotp - [ 3^{4 +2-4} ]
Dunque:
-8^6 : 2^{16} \cdotp - 3^2
Abbiamo il risultato singolo dei tre pezzettoni iniziali, che danno esponenti e basi diverse. Non possiamo fare niente se non usare la calcolatrice. Essa ci dice che le potenze scritte esplicitamente sono:
-262144 : 65536 \cdotp - 9 = 36
Fate fare alla calcolatrice in questi casi. Se non sapete come si fa basta fare “numero, poi cliccate ^, poi cliccate l’esponente”.
Gli esercizi svolti sono finiti, questi bastano per prendere un ottimo voto alla verifica in classe. La logica l’avete capita e non serve farne altri. Alla prossima! Se ci sono esercizi che volete approfondire o che non avete capito fatecelo sapere per email. Alla prossima!