FRAZIONI: tutto quello che c’è da sapere spiegato BENE!
Le frazioni sono un argomento complicato per gli studenti delle medie, poiché non intuitivo. In questa pagina vedremo TUTTO sulle frazioni. Non avrete bisogno di girovagare su internet, qua c’è tutto. Dalla base alle operazioni con le frazioni, fino ad esempi svolti e schemi. Mettetevi comodi e studiate questa pagina con calma. Un pomeriggio e sarete preparati sulle frazioni.
Indice
- Cosa è una frazione
- Come si semplifica una frazione
- Somma tra frazioni
- Sottrazione tra frazioni
- Moltiplicazione tra frazioni
- Divisione tra frazioni
- Potenza di una frazione
- Radice di una frazione
L’indice è abbondante, quindi state comodi e prendetevi una cioccolata calda! Partiamo dalla base, che cosa è una frazione e come è fatta?
Cosa è una frazione
Facciamo una considerazione: se avete un euro utilizzate il numero “1”, se avete tre euro utilizzate il numero “3”. Ma se volete scrivere mezzo euro come fate? Ecco il perché furono create le frazioni.
Cosa è una frazione? Una frazione è un insieme di due numeri, che rappresentano una “frazione” di qualcosa, o una “parte” di qualcosa.
Quindi, come facciamo a scrivere mezzo euro? Rappresentiamo con un disegno di un rettangolo verde il valore di 1 euro. Mezzo euro sarà la metà di questo rettangolo!
Come vedete mezzo euro viene rappresentato da una parte/ di due totali, del rettangolo verde.
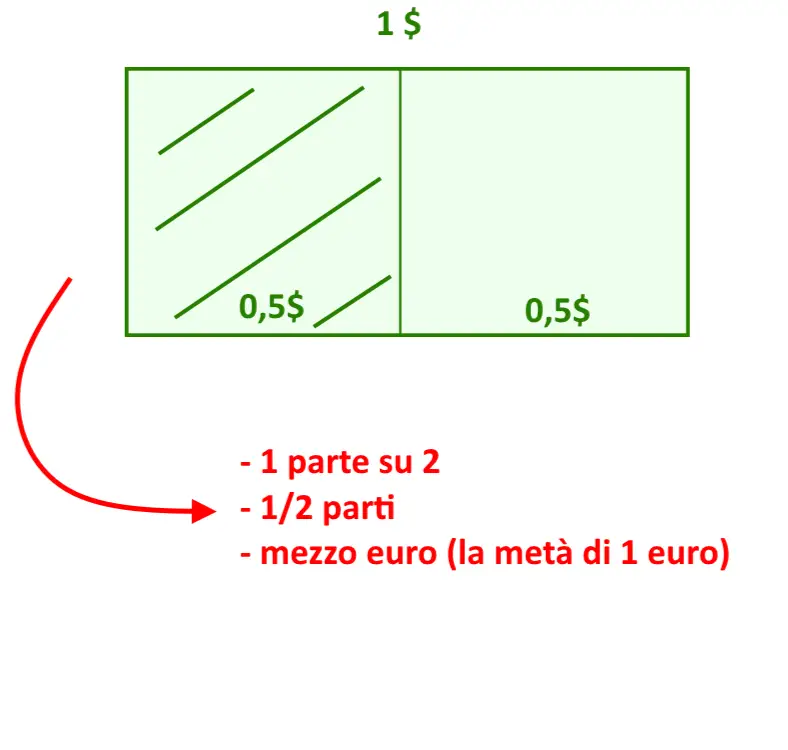
Quindi mezzo euro è 1/2 euro. Cioè una parte su due totali. Questa è la rappresentazione delle frazioni!
Scegliamo dunque di scrivere questo “1/2” nella maniera seguente, nella rappresentazione di una frazione.
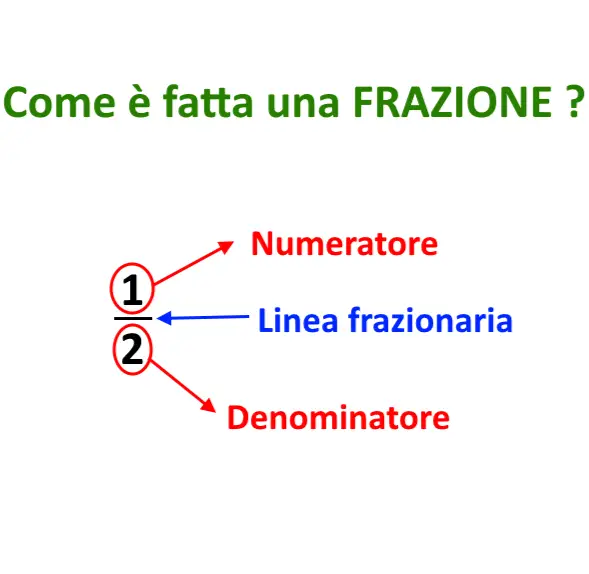
Il numero “1” lo mettiamo sopra (si chiama numeratore), il numero “2” lo mettiamo sotto (si chiama denominatore), mentre la linea “/” rappresenta proprio l’operazione di divisione!
Perché la linea della frazione è una divisione? Per rappresentare sempre il nostro solito “mezzo euro”, provate stesso voi a fare 1:2 alla calcolatrice, cosa viene fuori?
Viene fuori 0,5! Che se ci pensate è proprio quello che vale! Mezzo euro sarebbero 50centesimi, ossia 0,50 euro (cambiando l’unità di misura).
Vediamo subito alcuni esempi di frazioni, per capire come sono fatte!
Ora che abbiamo capito profondamente il significato e la rappresentazione di una frazione, passiamo a vedere alcuni calcolini che possiamo farci con esse.
Come si semplifica una frazione
Quando si ha a che fare con le frazioni, vi capiterà tantissime volte di “semplificare la frazione”: ora capiremo cosa è e come si fa. E’ un argomento importante, che vi servirà fino al quinto anno di Liceo ed oltre, quindi prendete appunti!
Introduciamo il concetto di “semplificare” con l’esempio seguente. Vediamo queste due frazioni diverse. Come potete notare però, rappresentano la stessa identica porzione! Anche se sono scritte diverse rappresentano la stessa quantità. Questo accade perché la frazione di sinistra ha inutilmente più porzioni, mentre quella di destra è “semplificata”!
Una frazione si dice semplificata se è irriducibile, ossia se non si può renderla ancora più “magra”.
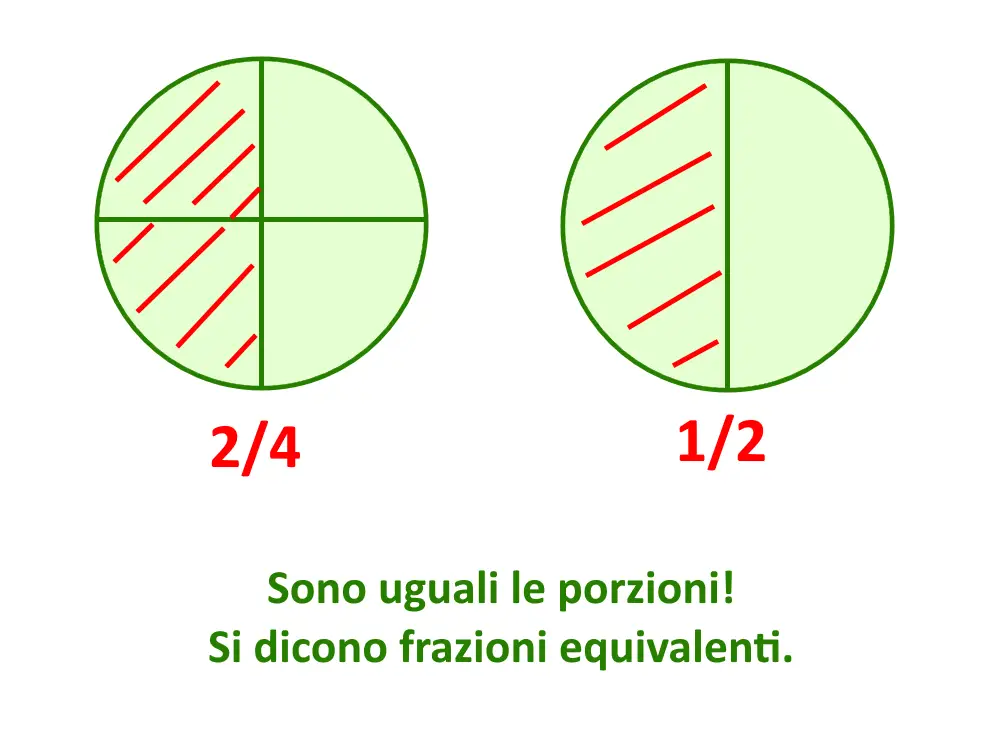
Abbiamo capito cosa significa quindi, ma in pratica come si semplifica una frazione? Come facciamo a passare da \frac{2}{4} a \frac{1}{2} ?
Il procedimento di semplificazione consiste nel:
- Trovare il divisore comune (qualsiasi)
- Dividere numeratore e denominatore per tale divisore.
Il primo passaggio consiste nel trovare un divisore, sapete che cosa è? Se lo sapete andate avanti, altrimenti leggete questi chiarimenti! Se ho un numero, ad esempio 9, cosa è un suo divisore? Un divisore di 9 è il 3, poiché 9:3=3, cioè da un numero naturale.
9:4=2,25 e quindi 4 non è divisore.
Partiamo dal nostro esempio:
\frac{2}{4}
Dobbiamo quindi trovare un divisore comune (cioè un numero che può essere diviso per il numeratore e denominatore).
Il numeratore ha come divisore 2, poiché 2:2=1 ed è ok!
Il denominatore ha come divisore 2 e 4, poiché 4:2=2 ok, e poi 4:4=1 ok.
Noi però dobbiamo prendere il divisore COMUNE, quello che hanno entrambi: cioè solo il 2!
Fatto questo primo passo, passiamo al secondo passaggio: dividere numeratore e denominatore per tale divisore (2).
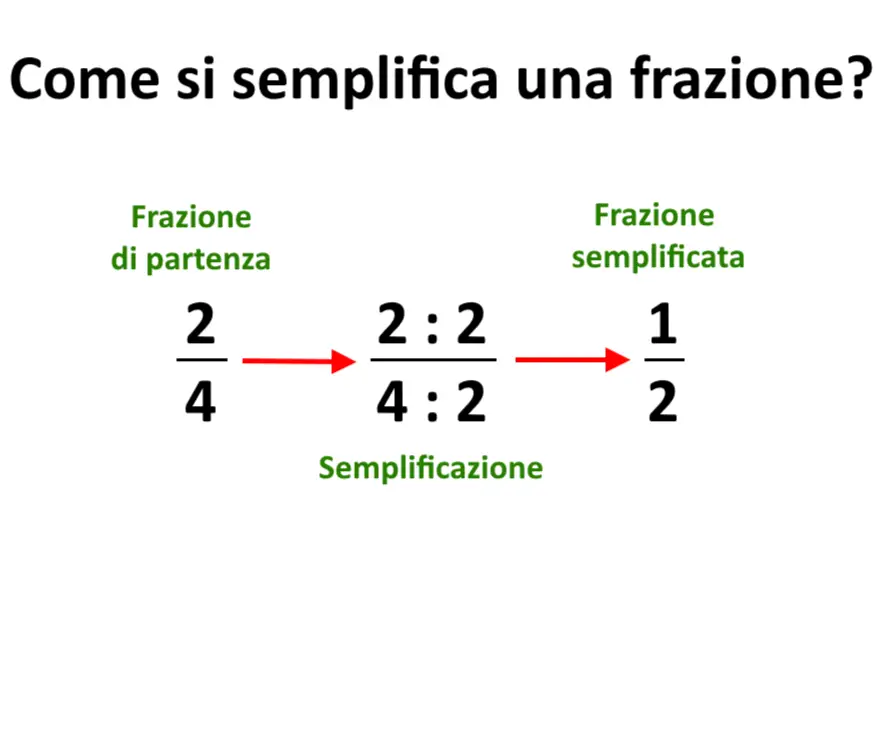
Il risultato è \frac{1}{2} , ed abbiamo semplificato la frazione!
Per allenarci, vediamo qualche esempio.
Esempio 1. Semplifica la frazione \frac{4}{18} .
Troviamo il divisore di 4. Come detto prima ha come divisori 2 e 4. Questo poiché 4:4=1 ok, poi 4:2=2 ok.
Non è divisore invece 3, perché se fate con la calcolatrice 4:3= 1,33333 che è un numero non naturale.
I divisori di 18 come li troviamo? E’ un numero grande. Quando abbiamo numeri difficili, basta partire da divisori bassi, come il 2. Non è importante trovarli tutti, basta che ne troviamo uno in comune!
Iniziamo quindi a dividere per 2 numeratore e denominatore:
\frac{4:2}{18:2} = \frac{2}{9}
Il numeratore ha come divisore solo 2, ora…il 9 lo possiamo dividere per 2? La risposta è no, quindi abbiamo finito di semplificare.
Esempio 2. Semplifica la frazione \frac{6}{18} .
Vedendo il 6 ed il 18, entrambi numeri pari, notiamo immediatamente che entrambi possono essere divisi per 2! Agli altri divisori poi ci pensiamo! Iniziamo però a semplificare:
\frac{6:2}{18:2} = \frac{3}{9}
Abbiamo finito l’esercizio di semplificazione? No. Ora invece notiamo che entrambi possono essere divisi per 3, facciamolo:
\frac{3:3}{9:3} = \frac{1}{3}
Ora sì che abbiamo semplificato completamente!
Abbiamo introdotto e capito cosa è una frazione, come semplificarla. Passiamo adesso a vedere tutte le operazioni in cui possono essere coinvolte le frazioni!
Somma tra frazioni
Vediamo ora come facciamo a fare una somma (addizione) fra due frazioni, come:
\frac{1}{3} + \frac{3}{2}
Come facciamo a farlo? La somma tra frazioni si fa col minimo comune multiplo. Molti di voi lettori non sanno cosa è un minimo comune multiplo, quindi ve lo spieghiamo passo dopo passo.
Il minimo comune multiplo consiste in un primo passaggio dove dobbiamo trovare il Massimo Comune Divisore. Questa sarà la prima cosa da fare.
Il “Massimo Comune Divisore” rappresenta il prodotto fra i divisori non comuni più grandi.
Quindi, prendiamo da parte i due denominatori: 3 e 2.
Troviamo i loro divisori. Il divisore unico del 3 è il 3!
Il divisore di 2 è solo 2!
Il Massimo comune divisore è la moltiplicazione fra i due divisori non comuni, quindi:
3 \cdotp 2 = 6
Il MCD è 6. Facciamo un secondo un altro esempio. Troviamo il MCD in:
\frac{1}{3} + \frac{3}{4}
Il divisore di 3 è solo 3.
I divisori di 4 sono: 2 e 4.
Il MCD è il prodotto fra 3 e 4 (perché dobbiamo prendere il più grande, visto che 2 è contenuto già dentro il 4 come divisore).
Torniamo dunque al nostro esempio iniziale:
\frac{1}{3} + \frac{3}{2}
Il suo MCD è: 6.
Per fare la somma dobbiamo fare il minimo comune multiplo. Come si fa? Dobbiamo iniziare a tracciare una lunga linea frazionaria, e poi mettere come denominatore il 6!
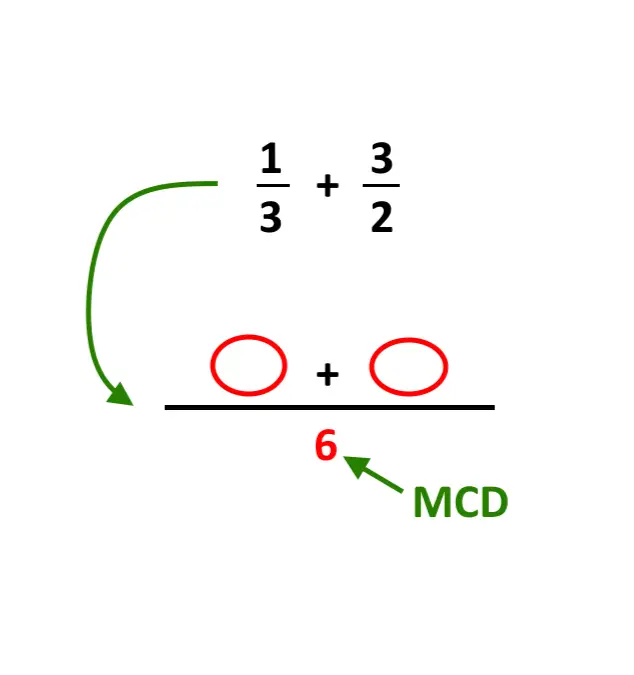
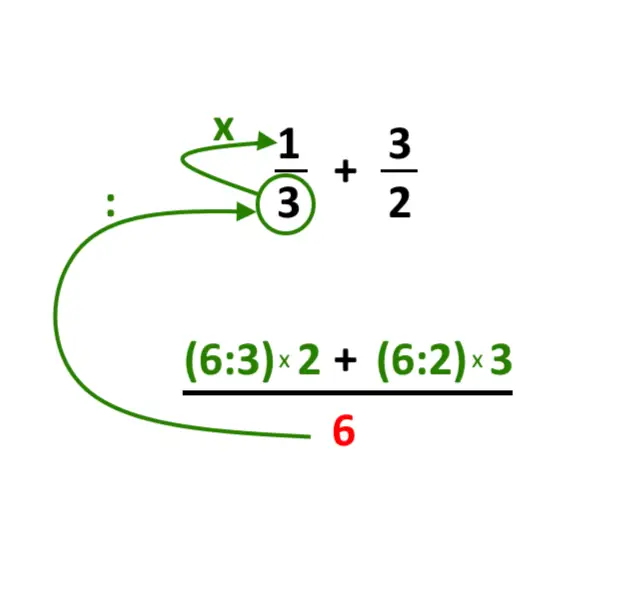
Dopo di che:
- Il primo termine al numeratore si ottiene facendo 6:3(denominatore della prima frazione) e poi moltiplicato per 1 (numeratore della prima frazione)
- Il secondo termine al numeratore si ottiene facendo 6:2(denominatore della seconda frazione) e poi moltiplicato per 3 (numeratore della prima frazione)
Fara la somma tra frazioni all’inizio è difficile, ma piano piano risulterà meccanico, fidatevi. Bisogna solo esercitarsi per 4 o 5 volte, e poi si inizia subito a prendere confidenza. Vediamo un altro esempio subito per capire meglio.
Esempio 1. Eseguire la somma \frac{1}{2} + \frac{2}{5}
Ok, ricapitoliamo: dobbiamo prima trovare il MCD. Il primo denominatore (2) ha come divisore solo il 2. Il secondo denominatore (5) ha come divisore solo 5.
Il MCD è quindi la moltiplicazione fra di essi: 2 \cdotp 5 = 10 .
Facciamo il minimo comune multiplo adesso:
\frac{1 \cdotp 5 + 2 \cdotp 2}{10}
Da cosa deriva quel 1 \cdotp 5 ? Deriva dall’avere fatto il minimo comune multiplo, cioè dall’aver fatto 10:2 (denominatore della prima frazione) che fa 5! E poi moltiplicare questo 5 per il numeratore della prima frazione (1)!
Stesso poi per la seconda frazione.
\frac{5 + 4}{10} = \frac{9}{10}
Essa non può essere semplificata, quindi lasciamo così.
Esempio 2. Eseguire la somma \frac{3}{4} + \frac{2}{3}
Troviamo il MCD. Il primo denominatore (4) ha come divisori: 2 e 4.
Passiamo al secondo denominatore: esso ha come divisore 2,3.
Il MCD risulterà essere 12.
Facciamo il mcm:
\frac{3 \cdotp 3 + 2 \cdotp 4}{12}
\frac{9 + 8}{12}
Facciamo la somma al numeratore:
\frac{17}{12}
Esempio 3. Eseguire la somma \frac{1}{2} + \frac{2}{3} + \frac{1}{5}
Ed ora come facciamo? Abbiamo la somma tra ben tre frazioni! La logica non cambia! Il procedimento è esattamente lo stesso, solamente che ora dobbiamo trovare il MCD fra non più due denominatori, ma tra tre.
Il primo denominatore ha come divisore 2.
Il secondo denominatore ha come divisore 3.
Il terzo denominatore ha come divisore 5.
Il MCD è la moltiplicazione tra tutti e tre! Quindi:
2 \cdotp 3 \cdotp 5 = 30
Non è cambiato nulla, vedete? Solamente l’aver aggiunto un nuovo termine. E questo concetto vale anche se abbiamo 5, 6 o più frazioni!
Facciamo il minimo comune multiplo, tra tre frazioni!
\frac{ 1 \cdotp 15 + 2 \cdotp 10 + 1 \cdotp 6 }{30}
\frac{ 15 + 20 + 6 }{30}
Di conseguenza, svolgendo l’addizione sopra:
\frac{ 41}{30}
Questa frazione non è semplificabile quindi va bene così.
Sottrazione tra frazioni
Abbiamo capito, nel paragrafo precedente, come si svolgono le somme tra due o più frazioni. Ma se abbiamo a che fare con la sottrazione tra frazioni come facciamo?
Fortunatamente non dobbiamo imparare nessun procedimento nuovo. Il tutto è proprio uguale, con una unica differenza: bisogna tenere il segno meno fra i termini, al numeratore. Vediamo subito un esempio per capire.
Svolgiamo la differenza in \frac{1}{2} - \frac{2}{3} .
Il primo passaggio è proprio uguale, sul cercare il MCD. In questo caso è 6. Senza alcuna differenza.
Vediamo il minimo comune multiplo, cosa c’è di nuovo. Facciamolo, dobbiamo però mettere il segno meno al numeratore corrispondente!
Svolgiamo la differenza in \frac{1 \cdotp 3 - 2 \cdotp 2 }{6} .
Vedete dove è stato inserito il segno meno. Il segno meno va messo nel termine corrispondente (il secondo in questo caso). Se abbiamo una differenza, tale differenza comparirà anche nel numeratore dopo il mcm!
\frac{ 3 - 4 }{6}
Se non sappiamo fare 3-4, facciamolo alla calcolatrice, è una differenza particolare! Esso darà -1.
\frac{ - 1 }{6}
Ora vi diciamo un’altra cosa molto utile. Il segno meno può essere portato davanti alla frazione:
- \frac{ 1 }{6}
L’esercizio è fatto!
Non c’è davvero nulla di diverso alla fine. Solo prestare una particolare attenzione sul dove è il segno meno. Vediamo comunque un esempio per consolidare questo concetto.
Esempio 1. Fare \frac{7}{2} - \frac{1}{2} - \frac{1}{3} .
Vediamo subito un qualcosa di non scontato, con tre frazioni. Questo esercizio vi farà capire completamente dove bisogna mettere i segni meno!
Il MCD è 6.
Svolgiamo il mcm. Vi do prima un indizio: Il segno meno sta prima del secondo termine, e del terzo termine. Di conseguenza dopo il mcm, dovremo avere un segno meno al secondo e terzo numero!
\frac{ 7 \cdotp 3 - 1 \cdotp 3 - 1 \cdotp 2 }{6}
\frac{ 21 - 3 - 2 }{6}
Fate un confronto fra questo risultato e la traccia iniziale, i segni meno stanno alla stessa identica posizione!
\frac{ 16 }{6}
Essa può essere semplificata, per 2 per esempio.
\frac{ 16 :2 }{6:2} = \frac{8}{3}
Ecco fatto!
Esempio 2. \frac{3}{2} - \frac{-1}{2}
Vediamo subito ora un esercizio difficile. Questo è da segnare, poiché è utile.
Senza guardare i numeri dentro le frazioni, notiamo che abbiamo un qualcosa del tipo:
\frac{...}{...} - \frac{...}{...}
Essa è una differenza tra due frazioni.
Troviamo il MCD che è 2.
Nel mcm, bisogna stare attenti, poiché avremo la moltiplicazioni fra due segni meno!
\frac{ 3 \cdotp 1 - (-1) \cdotp 1 }{2}
La parentesi quando si hanno due segni meno consecutivi è obbligatoria! Essa comporterà un cambio di segno: “meno per meno fa più”. Questo passaggio comporta spesso errori, quindi scrivete questo consiglio: quando ci sono più segni meno, mettiamo le parentesi, facciamo un passaggio in più, e non sbaglieremo.
\frac{ 3 +1 }{2}
\frac{ 4 }{2}
Semplifichiamo in:
\frac{ 4:2 }{2:2} = \frac{2}{1} = 2
Nell’ultimo passaggio abbiamo 2:1 che fa 2 (fatelo alla calcolatrice e verificate), e quindi lo possiamo anche scrivere come numero.
Una importantissima e ricorrente operazione è la moltiplicazione tra frazioni. Esse non sono difficili, quindi state tranquilli e leggete con calma!
Moltiplicazione tra frazioni
In questo paragrafo impareremo a svolgere le moltiplicazioni tra frazioni, che non rappresentano un problema, però ci sono alcune piccole cose che possono creare confusione, le vedremo tutte.
Il problema che ci poniamo è: come facciamo svolgere questa moltiplicazione?
\frac{2}{3} \cdotp \frac{7}{5}
La regola è una ed è semplice:
- Moltiplicare numeratore (prima frazione) per numeratore (della seconda frazione)
- Moltiplicare denominatore (prima frazione) per denominatore (della seconda frazione)
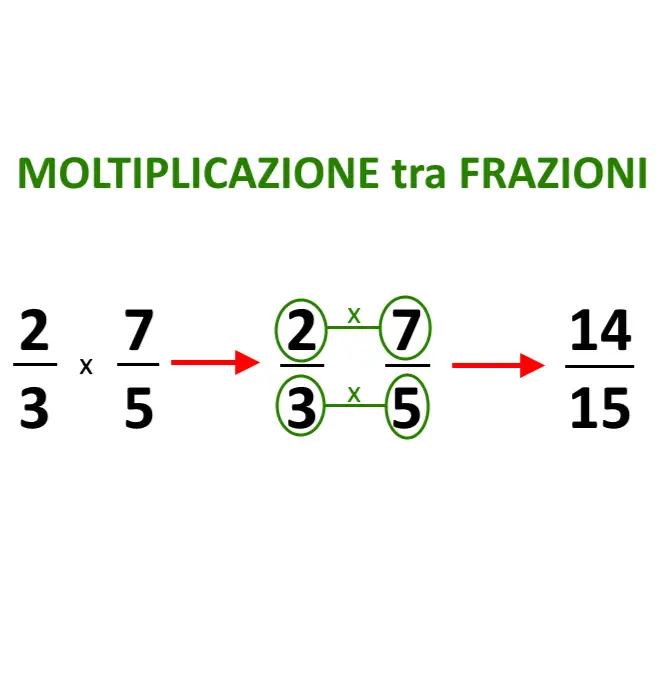
E’ davvero nulla di difficile quindi! Vediamo giusto un paio di veloci esempi su questa cosa, ma attenti perché il capitolo non è breve.
Proviamo a svolgere \frac{1}{3} \cdotp \frac{2}{4} . Seguendo la regola e lo schema presentato in precedenza verrà:
\frac{1 \cdotp 2}{3 \cdotp 4}
Facciamo le moltiplicazioni e viene:
\frac{2}{12}
Nulla di difficile, poi possiamo sempre semplificare:
\frac{2:2}{12:2} = \frac{1}{6}
Vediamo giusto un altro esempio, e poi passiamo avanti. Svolgiamo la moltiplicazione seguente:
\frac{4}{3} \cdotp \frac{10}{4}
Seguiamo la regola: moltiplicare i numeratori rispettivi e i denominatori rispettivi.
\frac{4 \cdotp 10 }{3 \cdotp 4}
\frac{40 }{ 12}
Fatto! Questa regola vale anche quando c’è una moltiplicazione con una frazione negativa! Seguiamo la stessa regola, ma semplicemente il segno meno rimane!
\frac{1}{3} \cdotp (-\frac{2}{3})
- \frac{1 \cdotp 2 }{3 \cdotp 3}
Svolgiamo sempre le moltiplicazioni, ma attenti a tenere sempre il segno meno fuori!
- \frac{2}{9}
Tutti consigli d’oro da segnare questi! Vediamo ora una cosa molto particolare: possiamo semplificare numeratore e denominatore direttamente, se sono uguali ad esempio!
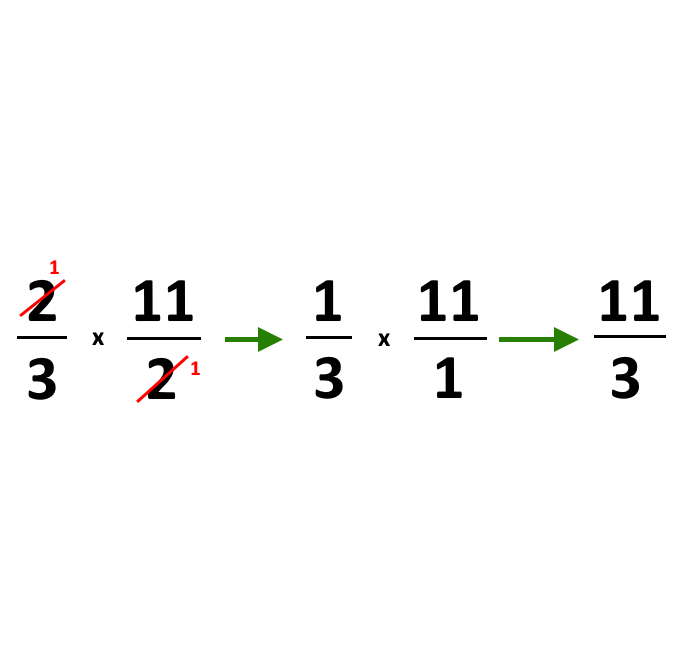
Si tratta di fare un passaggio in meno semplicemente. Piuttosto che svolgere la moltiplicazione e poi semplificare, possiamo semplificare già prima!
Questo vale anche se un numeratore col denominatore sono divisori! Vale quindi la stessa identica regola di semplificazione vista anche prima!
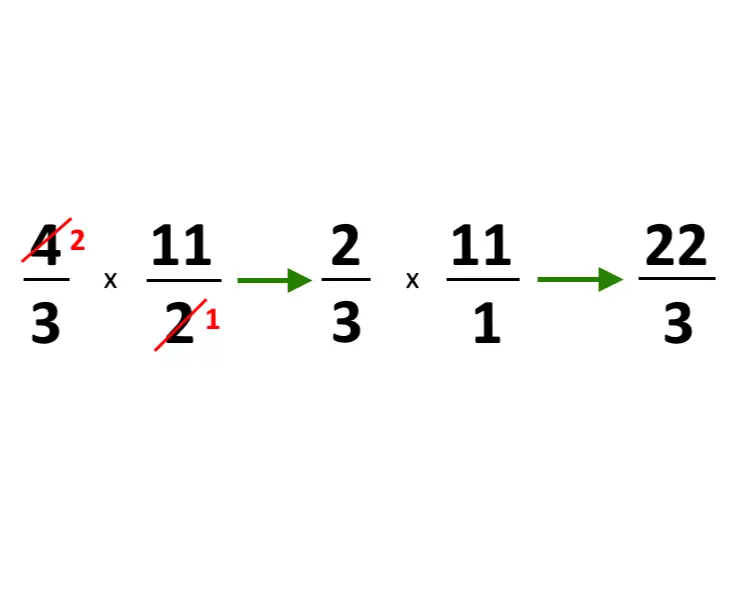
Abbiamo visto tutto sulle moltiplicazioni, passiamo all’operazione della divisione!
Divisione tra frazioni
La divisione tra frazioni fortunatamente capita raramente. E’ sicuramente la meno utile operazione. C’è da dire che però quando capita, moltissimi studenti non sanno come agire. In questo paragrafetto chiariremo i passaggi da fare quando siamo di fronte ad una divisione tra due frazioni!
Intendiamo una divisione tra frazioni, se abbiamo un qualcosa di questo tipo nell’immagine seguente.
Questa che vedete è anche detta “frazione di frazione”. Come agiamo? Iniziamo a distinguere il numeratore ed il denominatore di questa frazione gigantesca.
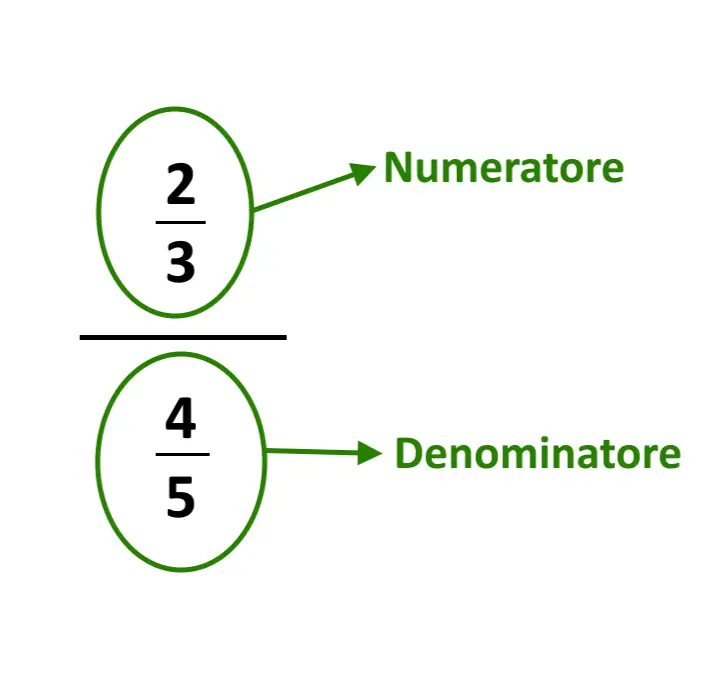
Dopo di che, scriviamo questa come moltiplicazione tra due frazioni. Scriviamo il numeratore uguale così com’è. Il secondo passo è moltiplicarlo per la frazione che sta giù, ma invertita!
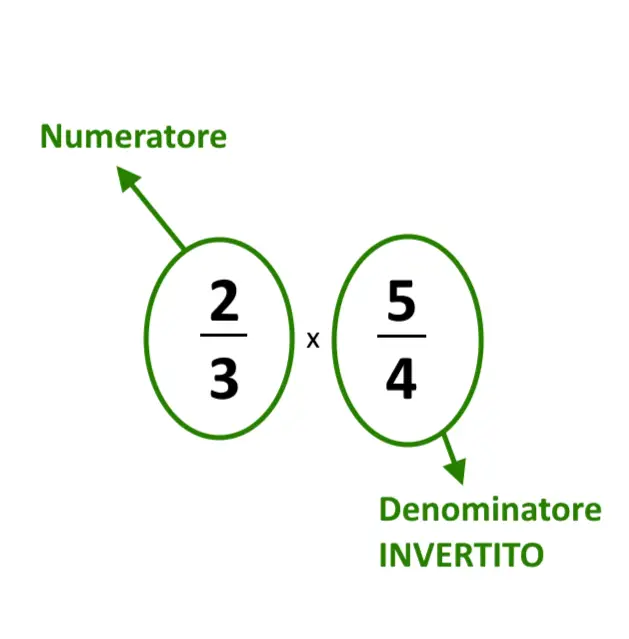
Questo è il passaggio da fare. Così ci siamo ricondotti al caso delle “moltiplicazioni tra frazioni”. Da qui in avanti sapete il risultato!
Non c’è niente da aggiungere, possiamo concludere così questo capitolo. Le operazioni principali le abbiamo finite, passiamo a quelle più complesse!
Potenza di una frazione
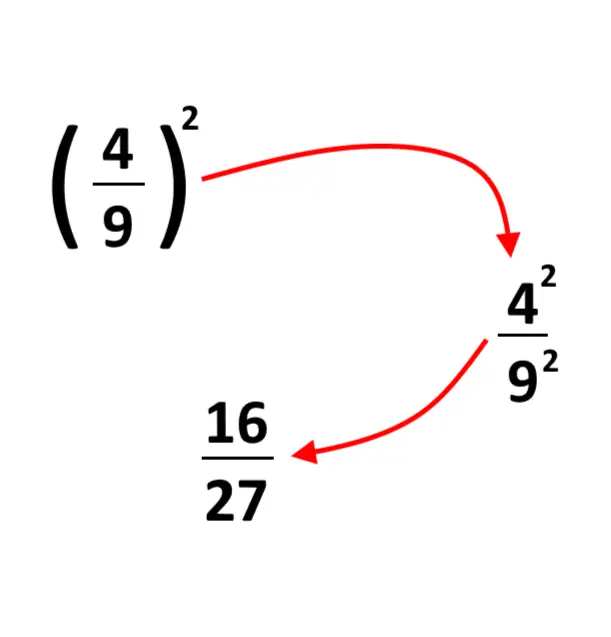
Per potenza di una frazione intendiamo il saper svolgere la seguente operazione:
( \frac{2}{3} )^2
Come vediamo TUTTA la frazione è elevata al quadrato (alla seconda). La domanda che ci poniamo è: come si fa? La risposta è immediata: portiamo la potenza al numeratore, e portiamo la stessa potenza al denominatore, scritte separate:
\frac{2^2}{3^2}
Da qui, semplicemente scriviamo per esteso il valore di quelle due potenze. Partiamo dal numeratore, dove abbiamo:
2^2 = 2 \cdotp 2 = 4
E poi al denominatore si ha:
3^2 = 3 \cdotp 3 = 9
Il risultato finale, della potenza di una frazione ci dà una semplice frazione:
\frac{4}{9}
Non è davvero per nulla complicato. Ricapitolando, partendo da una potenza, portiamo la potenza al numeratore e denominatore e svolgiamo. Vediamo alcuni esempi, per consolidare meglio.
Vi consiglio solo di stare attenti alla potenza di un segno meno:
( - \frac{1}{3} )^2
Ci siamo bloccati? Non bisogna aver paura. La frazione l’abbiamo capito, ma quel segno meno dove lo mettiamo? La potenza va anche al segno meno! Quindi ne risulterà:
(-)^2 \cdotp \frac{1^2}{3^2}
Quindi si aggiunge un termine moltiplicato vicino, poi per il resto è uguale.
Sappiamo che un segno meno al quadrato (meno per meno) fa più, quindi esso poi se ne va:
\frac{1^2}{3^2}
E ci siamo ricondotti al caso di prima, svolgiamo le potenze ed abbiamo fatto!
\frac{1}{9}
E se invece abbiamo una potenza alla terza? Se abbiamo una potenza alla terza o diversa, la logica da seguire è la stessa:
( \frac{4}{5} )^3
La potenza va sempre al numeratore e denominatore, separate:
\frac{4^3}{5^3}
E svolgiamo. Se non avete mai visto una potenza alla terza, è sempre come:
4^3 = 4 \cdotp 4 \cdotp 4 = 64
Il risultato è la frazione semplice:
\frac{64}{125}
Caso di particolare interesse e dubbi è quando abbiamo anche un segno meno elevato alla terza, come:
(- \frac{1}{2} )^3
Facciamo proprio quello che abbiamo fatto prima, quindi c’è la solita frazione alla terza, e poi si aggiunge vicino un termine che è il segno “-” elevato alla terza:
(-)^3 \frac{1^3}{2^3}
Il segno meno elevato alla terza sarebbe:
-^3 = - \cdotp - \cdotp - = + \cdotp - = -
Qui, una regola da ricordare:
- Segno “-” elevato alla numero pari, ci dà un segno “+” (per es. -^4 = +)
- Segno “-” elevato alla numero dispari, ci dà un segno “-” (per es. -^3 = -)
Per le potenze abbiam visto tutto, se rimane qualche dubbio fatecelo sapere per email! Passiamo alle radici, l’ultima operazione in cui sono coinvolte le frazioni!
Radice di una frazione
Partiamo da un presupposto molto importante, che vi può aiutare a capire facilmente e senza sforzo come si fa la radice di una frazione. Dovete sapere che, per chi non se lo ricordasse, la radice è una potenza. Ricordiamo a tal proposito la seguente proprietà.
\sqrt[2]{3} = 3^{\frac{1}{2} }E questo cosa significa? Che la logica è proprio uguale a quella adottata per una potenza di una frazione!
Se lì dicevamo che dovevamo applicare la potenza singola al numeratore e poi al denominatore, qui uguale: dobbiamo applicare la radice al numeratore e poi al denominatore separati!
Se pensate di aver capito tutto e di voler skippare, non ve lo consiglio. Gli esempi servono sempre per consolidare la teoria. Inoltre, noi di MondoFisica, vediamo sempre esempi particolari che fanno imparare cose nuove.
Applichiamo subito il concetto visto, con tale esercizio:
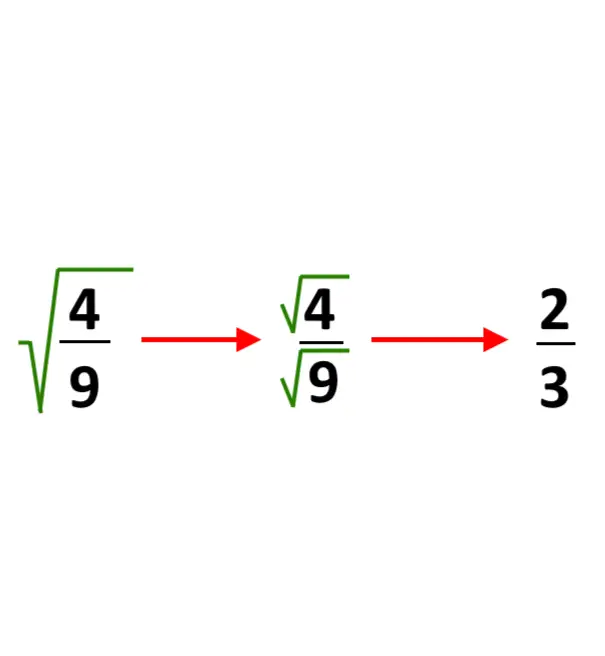
\sqrt{ \frac{4}{3} }
Abbiamo detto che 1) applichiamo a numeratore e denominatore la radice, singolarmente.
\frac{ \sqrt{4} }{ \sqrt{3} }
Esercizio finito? No. Osserviamo sempre ciò che abbiamo, prima di giungere a conclusioni affrettate. La radice di 4 quanto fa? Fa 2! Se non lo sapete, prendete la calcolatrice e provate! E allora scriviamolo! E’ sempre meglio scrivere un numero pulito, piuttosto che una radice.
La radice di 3 invece quanto fa? Fa un numero strano, quindi lo lasciamo così com’è!
\frac{ 2 }{ \sqrt{3} }
Ecco fatto! A questo punto si preferisce non tenere la radice al denominatore e la si porta con la “razionalizzazione” sopra (non sappiamo nemmeno noi il perché).
La razionalizzazione consiste brevemente nel moltiplicare e dividere per la radice che compare al denominatore ( \sqrt{3} ). Questo processo serve per “portare” la radice sopra al numeratore.
\frac{ 2 }{ \sqrt{3} } \cdotp \frac{ \sqrt{3}}{ \sqrt{3}}
Ricordate che moltiplicare e dividere per una stessa quantità si può perché non cambia il risultato finale!
Al denominatore, c’è la moltiplicazione tra due radici. Sappiamo che:
\sqrt{3} \cdotp \sqrt{3} = 3
Di conseguenza il risultato che vi porterà il libro è sicuramente:
\frac{ 2 \sqrt{3} }{3}
Passiamo ad un altro esempio, con una radice di indice 3. La logica è sempre uguale.
\sqrt[3]{ \frac{8}{27} }
Quindi, portiamo per prima cosa la radice sopra e sotto.
\frac{ \sqrt[3]{8} }{ \sqrt[3]{27} }
Ed ora? Calcolatrice: shift + (c’è la radice terza in giallo) e poi inserite il numero. Se non avete una calcolatrice scientifica, leggete il nostro articolo su quale calcolatrice prendere su Amazon!
Scriviamo il risultato:
\frac{ 2 }{ 3 }
I giochi son fatti.
La pagina è molto lunga, ma è davvero esaustiva in tutte le forme che possiede l’argomento della frazione. Se però abbiamo mancato qualcosa, o volete approfondire (anche qui), ditecelo per email e noi provvederemo!