Come trovare il punto di intersezione tra due rette
Come trovare il punto di intersezione tra due rette: ESERCIZI SVOLTI. Determineremo il punto di intersezione di due rette mostrando esempi con soluzioni ed esercizi svolti di diverso tipo, così da essere assolutamente preparati per la futura verifica in classe! Troverete tutto in questa pagina, spiegato con cura e con calma!
Indice
- Come si calcola il punto di intersezione?
- I 3 casi che possono capitare
- Come determinare punto di intersezione: ESERCIZI
Iniziamo ad inquadrare la situazione, vedendo il procedimento generale che seguiremo per calcolare e trovare il punto di intersezione tra due rette.
Come si calcola il punto di intersezione di due rette?
In un piano cartesiano vi sono due rette r ed s di equazioni:
r: \; y=mx+q
s: \; y=m'x+q'
Se non vi ricordate, questa sopra comunque è la forma esplicita generale di una retta nel piano cartesiano. Tornando a noi, queste due rette saranno posizionate nel piano cartesiano, per esempio, come segue.
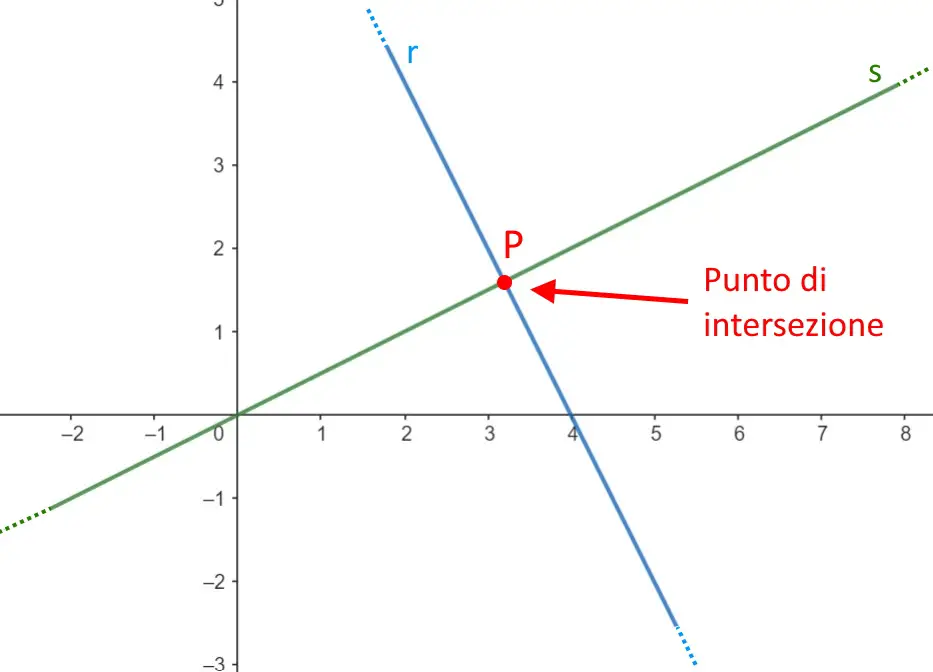
L’obiettivo è come si trova questo punto di intersezione?
Come prima cosa mettiamo a sistema le due equazioni delle rette:
\begin{cases} y=mx+q \\ y=m'x+q' \end{cases}
Il punto di intersezione sarà dato dalla risoluzione del sistema, trovando un valore delle due variabili (x,y). Risolviamo il sistema per sostituzione, quindi sostituiamo la y della prima equazione nella seconda, lasciando la prima così com’è:
\begin{cases} y=mx+q \\ mx+q=m'x+q' \end{cases}
Ora ci concentriamo solo sulla seconda equazione: se notate, essa è di fatti una semplice equazione di primo grado. Possiamo quindi risolverla trovando la x. Portiamo quindi i termini con la x a primo membro, ed il resto a secondo membro:
\begin{cases} y=mx+q \\ mx-m'x=+q' -q \end{cases}
(Con gli esercizi svolti dell’ultima sezione, tutto vi sarà estremamente più chiaro! Un po’ di pazienza, cercate solo di capire il ragionamento che starà dietro)
\begin{cases} y=mx+q \\ (m-m') x=+q' -q \end{cases}
Isoliamo la x a sinistra, dividendo tutto per m-m’. Così facendo abbiamo finalmente trovato la componente x del punto di intersezione!
\begin{cases} y=mx+q \\ x=\frac{q' -q }{m-m'} \end{cases}
Ora che abbiamo trovato la x, la sostituiamo nella prima equazione. Così facendo troveremo anche la componente y del punto di intersezione, ed i giochi saranno fatti!
\begin{cases} y=m\frac{q' -q }{m-m'}+q \\ x=\frac{q' -q }{m-m'} \end{cases}
Il problema è risolto! Chiaramente in un esercizio ci saranno dei numeri, e quindi vi verrà un qualcosa del tipo:
\begin{cases} y=3 \\ x=2 \end{cases}
E questo (2,3) sarà il punto P di intersezione!
I tre casi che possono capitare
Non sempre il sistema
\begin{cases} y=mx+q \\ y=m'x+q' \end{cases}
porta ad una soluzione. Di fatti possono capitare tre casi diversi:
- Rette incidenti
- Rette parallele
- Rette coincidenti
Vediamoli uno per uno con calma (nulla di complicato).
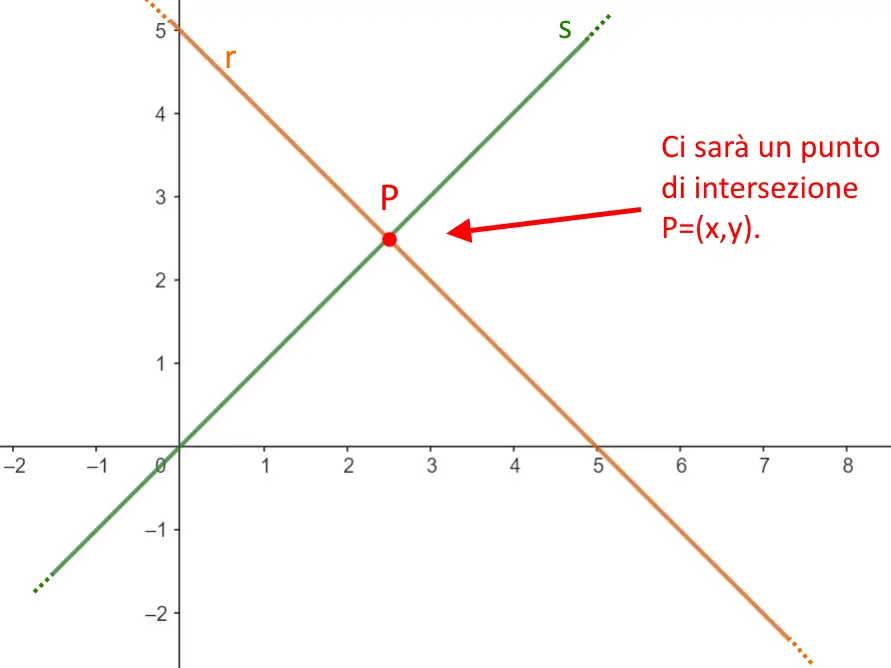
Intersezione con rette incidenti
Quando le rette hanno il coefficiente angolare m \ne m' allora le rette si incontrano in un punto di intersezione P, e il sistema porta ad una soluzione ad esempio del tipo P=(1,2).
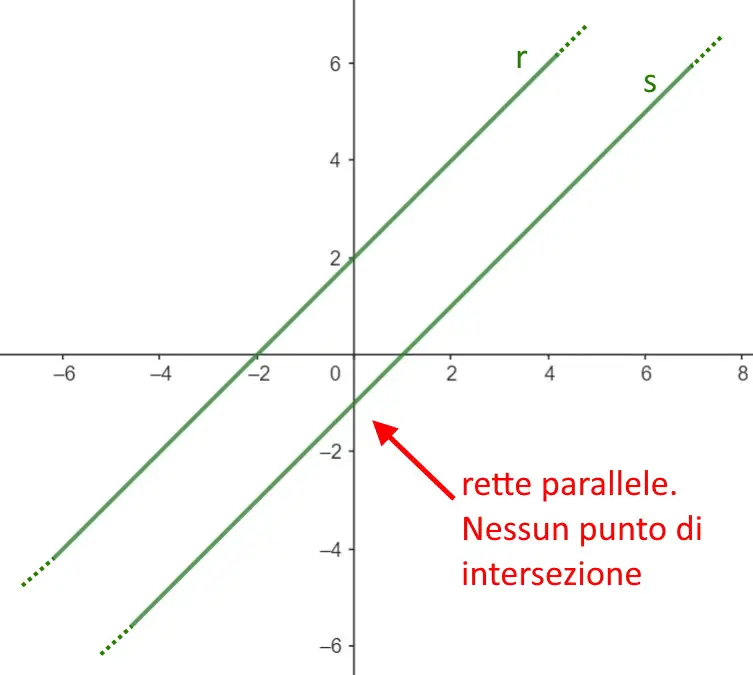
Intersezione con rette parallele
Se le rette hanno il coefficiente angolare uguale m = m' le rette sono parallele. Quindi non c’è proprio bisogno di risolvere il sistema perché non porterà mai ad una soluzione! Diremo fin da subito che le rette sono parallele e non c’è nessun punto di intersezione fra le due.
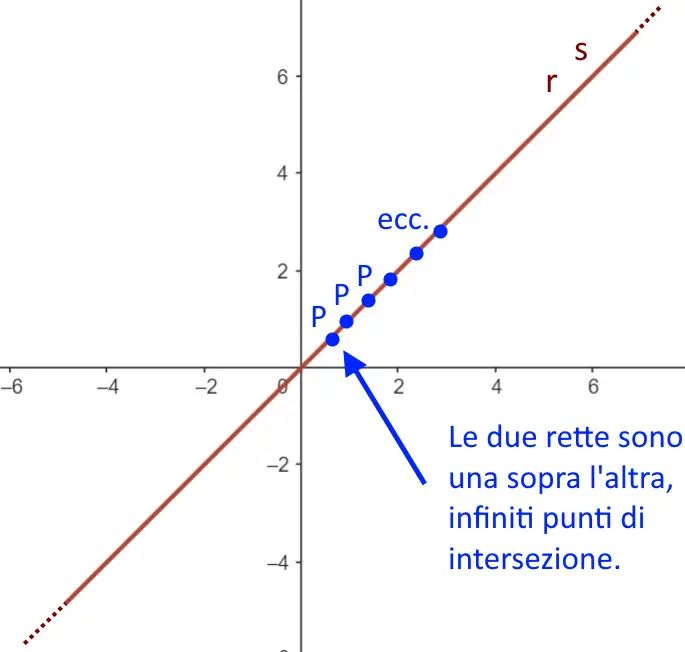
Intersezione con rette coincidenti
Se le rette hanno coefficiente angolare uguale m = m' ed in più hanno anche il termine noto uguale q = q' significa che le due rette sono coincidenti, ossia una sopra l’altra. Avremo quindi infiniti punti di intersezione. Anche in questo caso non ci sarà bisogno di fare nessun calcolo e risolvere nessun sistema, basta vedere queste due uguaglianze per poterlo dire fin dall’inizio.
Per capire meglio, vediamo subito degli esercizi svolti su come trovare un punto di intersezione fra due rette: non è nulla di complicato fidatevi!
Come determinare punto di intersezione di due rette
ESERCIZI SVOLTI
Esercizio 1. Calcolare il punto di intersezione delle due rette di equazioni r: y=-2x+2 ed s: y=3x-3.
Come detto, per prima cosa mettiamo a sistema le due equazioni delle rette:
\begin{cases} y=-2x+2 \\ y=3x-3 \end{cases}
Adesso prima di procedere nella risoluzione del sistema, controlliamo che m\ne m' e di fatti abbiamo che -2 \ne 3 . Quindi le due rette non sono parallele, e di conseguenza avranno un punto di intersezione! Risolviamo il sistema per sostituzione, mettendo la prima y nella seconda equazione del sistema:
\begin{cases} y=-2x+2 \\ -2x+2=3x-3 \end{cases}
Risolviamo la seconda che è una equazione di primo grado, dove vogliamo trovare la x. Portiamo le x a primo membro:
\begin{cases} y=-2x+2 \\ -2x-3x=-2-3 \end{cases}
Sommiamo i rispettivi termini:
\begin{cases} y=-2x+2 \\ -5x=-5 \end{cases}
Cambiamo tutto di segno e dividiamo per 5:
\begin{cases} y=-2x+2 \\ x=1 \end{cases}
La componente x del punto di intersezione è stata trovata! Adesso sostituiamo questo valore nella prima equazione:
\begin{cases} y=-2 \cdotp 1+2 \\ x=1 \end{cases}
\begin{cases} y=0 \\ x=1 \end{cases}
Il sistema è ora risolto. Il punto di intersezione delle due rette è il punto P= (1,0). Ricordatevi chiaramente che va sempre prima la x e poi la y nella scrittura di un punto P=(x,y).
Esercizio 2. Calcolare il punto di intersezione delle due rette di equazioni r: 4x-3y-2=0 ed s: -8x+6y-1=0.
Come sempre mettiamo subito a sistema le due equazioni:
\begin{cases} 4x-3y-2=0 \\ -8x+6y-1=0 \end{cases}
Le due equazioni come vedete sono scritte in forma implicita. Noi per comodità le vogliamo nella forma classica, quella esplicita, come nel precedente esercizio. Trasformiamo quindi in forma esplicita queste due rette. Teniamo quindi solo la y a sinistra nel primo membro.
\begin{cases} -3y=-4x+2 \\ +6y=8x+1 \end{cases}
Isoliamo le y dividendo per -3, e per 6:
\begin{cases} y=\frac{4}{3}x- \frac{2}{3} \\ y=\frac{8}{6}x+ \frac{1}{6} \end{cases}
\begin{cases} y=\frac{4}{3}x- \frac{2}{3} \\ y=\frac{4}{3}x+ \frac{1}{6} \end{cases}
Adesso controlliamo i coefficienti angolari. Notiamo che:
m = m' \implies \frac{4}{3} = \frac{4}{3}
Le due rette sono parallele, non c’è nessun punto di intersezione. Non c’è bisogno di risolvere il sistema. Notiamo inoltre che i due termini noti non sono uguali, quindi le due rette sono solo parallele.
Esercizio 3. Calcolare il punto di intersezione delle due rette di equazioni r: -x+y-6=0 ed s: x-y+6=0.
Prima cosa: mettere a sistema le due equazioni delle rette.
\begin{cases} -x+y-6=0 \\ x-y+6=0 \end{cases}
Come prima, le due rette sono scritte in forma esplicita, noi però le vogliamo in forma esplicita classica per comodità. Facciamo gli stessi passaggi di prima…provate voi da soli!
\begin{cases} y=x+6 \\ -y=-x-6 \end{cases}
Cambiamo tutto di segno nella seconda equazione:
\begin{cases} y=x+6 \\ y=x+6 \end{cases}
Come possiamo immediatamente notare le due equazioni hanno i coefficienti angolari uguali (1=1) ed anche i termini noti perfettamente uguali (6=6). Di conseguenza non bisogna risolvere nessun sistema, perché le rette sono coincidenti: ossia una sopra l’altra, quindi i punti di intersezione saranno infiniti.
Esercizio 4. Calcolare il punto di intersezione delle due rette di equazioni r: y=2x-1 ed s: y=3.
Mettiamo a sistema le due rette:
\begin{cases} y=2x-1 \\ y=3 \end{cases}
(Nella seconda equazione non compare la x perché è una retta parallela all’asse x, è una particolare retta quindi). Le due rette sono incidenti (2 \ne 0 ) e quindi ci sarà un punto di intersezione. Visto che abbiamo già la componente y del punto P di intersezione che sarà certamente P=(?,3), sostituiamo la seconda nella prima! Questo perché la seconda equazione è già risolta, non c’è nessuna x da calcolare lì!
\begin{cases} 3=2x-1 \\ y=3 \end{cases}
\begin{cases} -2x=-3-1 \\ y=3 \end{cases}
Cambiamo di segno e dividiamo per 2:
\begin{cases} x=\frac{3}{2}+\frac{1}{2} \\ y=3 \end{cases}
\begin{cases} x=\frac{3+1}{2} \\ y=3 \end{cases}
Quindi:
\begin{cases} x=2 \\ y=3 \end{cases}
Il punto di intersezione di queste due rette è P=(2,3).
Esercizio 5. Calcolare il punto di intersezione della retta di equazione r: y=x ed una retta s che è perpendicolare ad r e che passa per il punto A=(0,1).
La seconda equazione non ce l’abbiamo, dobbiamo trovarla. Sappiamo però che essa è perpendicolare ad r, ed è passante per il punto un punto A.
L’obiettivo è trovare:
s: \; y=mx + q
Essendo le due rette perpendicolari, allora segue che:
1= - \frac{1}{m} \implies m= -1
Ora che sappiamo il coefficiente angolare, applichiamo la formula della retta passante per un punto.
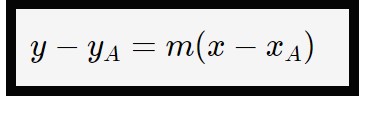
Nel nostro caso, sostituendo le componenti del punto A:
y - 1 = -1 (x-0)
y - 1 = -x \implies s: \; y=-x+1
Trovata la seconda equazione, possiamo trovare il punto di intersezione fra le due rette.
\begin{cases} y=x \\ y=-x+1 \end{cases}
\begin{cases} y=x \\ x=-x+1 \end{cases}
Troviamo la x nella seconda equazione:
\begin{cases} y=x \\ 2x=+1 \end{cases}
\begin{cases} y=x \\ x=\frac{1}{2} \end{cases}
Sostituiamo tale valore nella prima equazione trovando così le due componenti del punto P di intersezione!
\begin{cases} y=\frac{1}{2} \\ x=\frac{1}{2} \end{cases}
Segue che P=(\frac{1}{2} ,\frac{1}{2} ) .
Può capitare nella verifica in classe che vi si chiedi anche di trovare l’equazione della retta stessa. Vi consiglio perciò di rivedervi come trovare l’equazione di una retta, rette parallele, rette perpendicolari.
Abbiamo visto in questa pagina come trovare il punto di intersezione fra due rette.
Trovate altre centinaia di esercizi svolti sul sito MondoFisica sia di matematica, che di geometria analitica e geometria!
Per approfondire:
https://it.wikipedia.org/wiki/Retta_nel_piano_cartesiano
rette sono
perpendicolari
di
rette