Fascio di rette: formule ed esempi spiegati
In questa pagina definiremo un fascio di rette: fascio che sarà proprio o improprio. Inoltre vedremo i fasci generati da due rette. Mostreremo poi via via esempi spiegati passo dopo passo. Ci saranno dunque anche degli esercizi svolti.
Indice
Un fascio di rette è un insieme di tutte le possibili rette, che si ottengono facendo variare il coefficiente angolare (fascio proprio) o il termine noto (fascio improprio). Ora le vedremo meglio una per una con precisione!
Fascio di rette proprio
Il fascio di rette proprio è l’insieme di tutte le rette che passano per uno stesso punto P. Noi siamo in Geometria Analitica, quindi queste rette devono avere le caratteristiche di una funzione. La retta verticale evidenziata in rosso non è una funzione, quindi la escludiamo dall’insieme di rette (non fa parte del fascio).
Perché la retta verticale non è una funzione? Perché per una sola x associa tante y, e ciò non è la definizione di funzione.
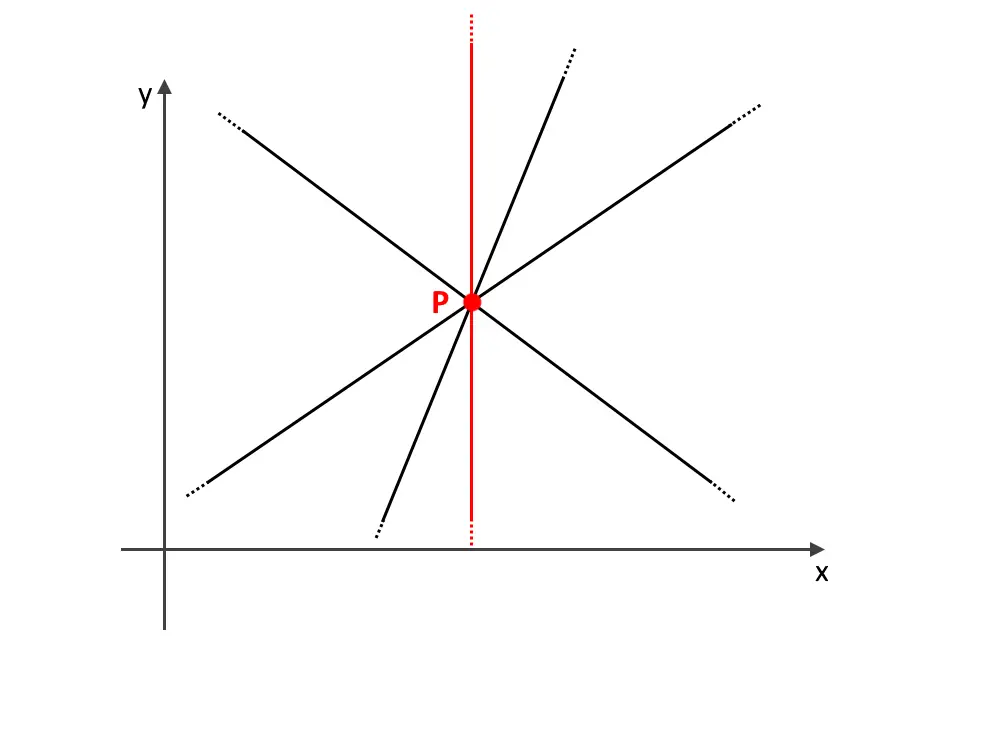
Questo è detto fascio di rette proprio.
Equazione del fascio di rette proprio
Vediamo insieme l’immagine di sopra: l’unica cosa che varia nelle queste rette è la diversa angolazione, cioè una retta ha più pendenza ed un’altra ne ha meno, e così via. Diversa angolazione si traduce, in geometria analitica, in un diverso coefficiente angolare m!
Di conseguenza l’unica cosa che non ha un valore fisso è proprio m! Perciò lo lasciamo così com’è: come una variabile. L’equazione di un fascio di rette proprio è quindi la seguente.

Se difatti proviamo a sostituire diversi valori di m, otteniamo diverse rette, tutte passanti per lo stesso punto P.
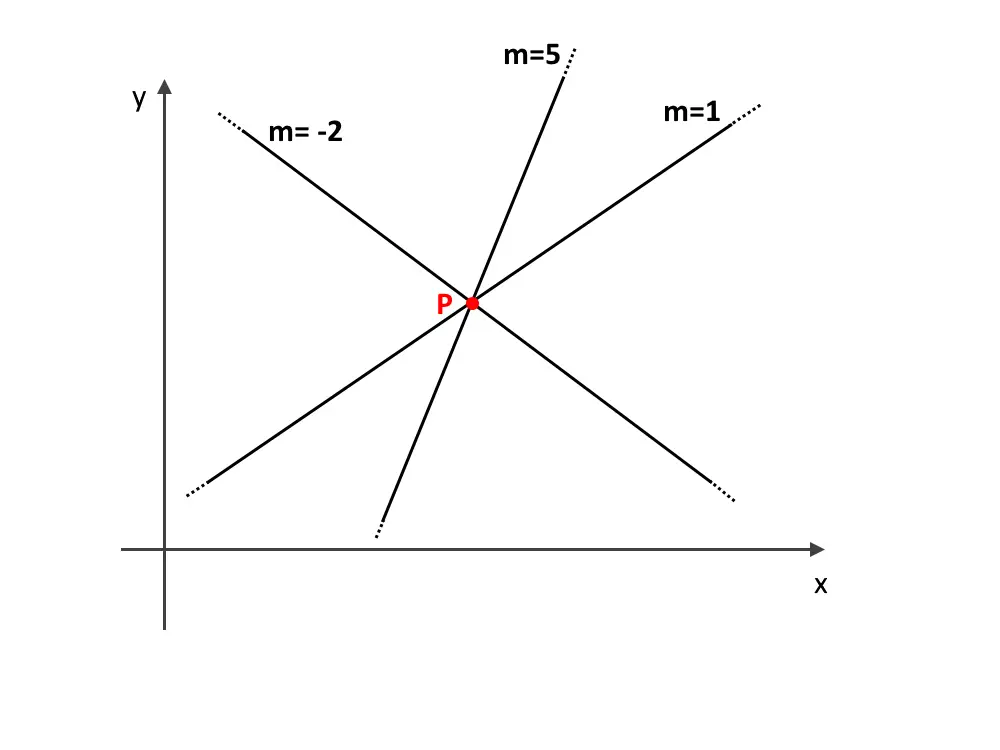
Sostituire un certo valore di m (ad esempio m=2), significa fare la seguente cosa:
y-y_P = m (x-x_P) \implies y-y_P = 2 (x-x_P)
Se poi vogliamo il fascio completo, ossia comprendendo anche la retta verticale che ricordiamo non essere una funzione, si scrive così:
y-y_P = m (x-x_P) \land x=x_P
Dove con quella scrittura aggiuntiva indichiamo appunto quella retta.
Centro del fascio di rette proprio
Abbiamo detto che l’equazione di un fascio di rette proprio è il seguente:
y-y_P = m (x-x_P)
Quei due numeri x_P, y_P sono le coordinate del centro del fascio. Come potete vedere se assegniamo diversi valori di m, x_P, y_P non cambiano: il centro di un fascio rimane sempre lo stesso.
Il centro del fascio è quindi il seguente.
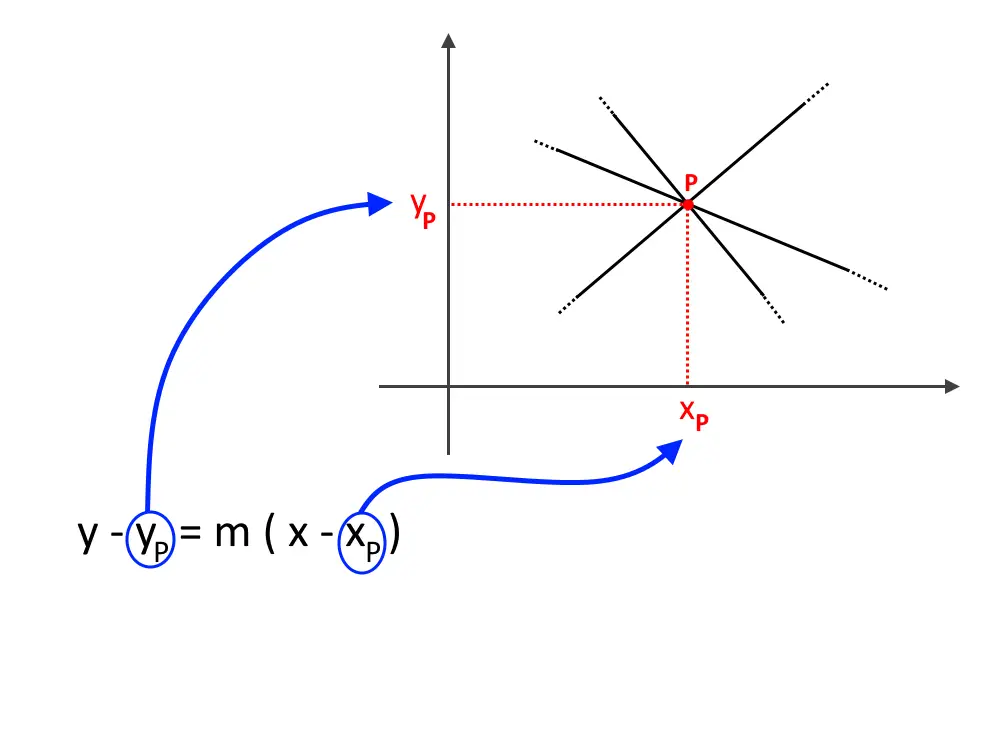
Facciamo qualche esempio, perché i segni potrebbero confondere, ma ora li vediamo insieme.
Esempio 1. Qual è il centro del fascio di equazione y-2 = m (x-3) ?
Facendo il confronto fra l’equazione, e le componenti del centro del fascio, notiamo che:
y-y_P = m (x-x_P)
y-2 = m (x-3)
Deduciamo che il centro del fascio è:
P=(3,2)
Ciò che può confondere è quando compaiono dei +! Vediamo.
Esempio 2. Qual è il centro del fascio di equazione y+2 = m (x-1) ?
Il centro del fascio qui è invece:
P=(1,-2)
Perché questo? Che ragionamento dobbiamo fare? Partiamo dalla formula dell’equazione del fascio, e quella del nostro esercizio:
y-y_P = m (x-x_P)
y+2 = m (x-1)
Come potete vedere dovremmo avere un – (componente y di P), e invece abbiamo un +! Quindi scriviamo così:
y-y_P = m (x-x_P)
y-(-2) = m (x-1)
Ed ora figura benissimo che la componete dell’ordinata del fascio è -2!
Esempio 3. Consideriamo il fascio di rette di equazione y-1 = m (x-1) . La retta parallela all’asse x che valore di m ha? E quella parallela all’asse y?
Partiamo da quella parallela all’asse y, essa è una retta verticale, ed all’inizio l’abbiamo indicata in rosso perché non era una funzione. Come detto alla fine della sezione precedente essa ha come equazione (equazione non significa funzione):
x=x_P \implies x=1
Invece, quella parallela all’asse x è una funzione! Una funzione costante per la precisione. Per trovare questa invece bisogna porre m=0! Otteniamo quindi:
y-1 = 0 \cdotp (x-1) \implies y-1=0 \implies y=1
E questa invece è la retta del fascio parallela all’asse delle x. Questi due sono dei casi particolari che potrebbero capitarvi come domande nel compito in classe.
Fascio di rette improprio
Un fascio di rette improprio è l’insieme di tutte le rette parallele fra di loro. Quindi è un insieme di rette con lo stesso coefficiente angolare. Qui, la variabile è il termine noto q!
Perché stesso coefficiente angolare? Se notate nella figura successiva, le rette hanno la stessa pendenza, stessa angolazione, quindi hanno stesso coefficiente angolare m.
Sostituendo diversi valori di q, otteniamo diverse rette del fascio. Il termine noto q infatti è responsabile del “far traslare una stessa retta” verso l’alto o il basso.
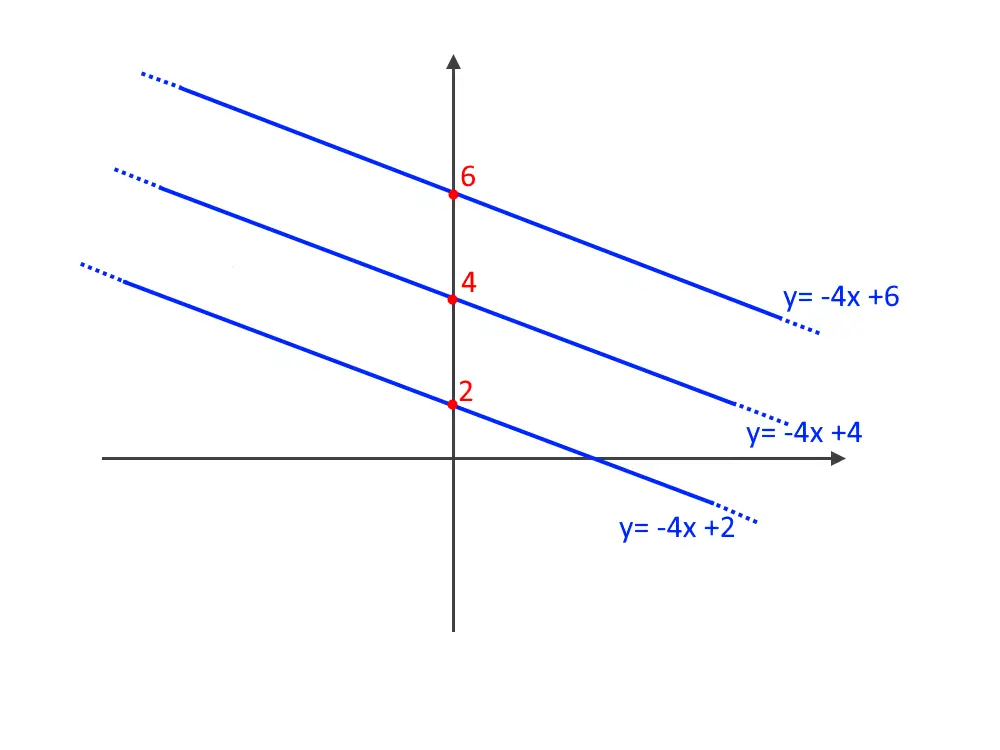
Questo è un fascio di rette improprio. Come vedete non possiede un centro.
Equazione del fascio di rette improprio
Questo fascio, ossia l’insieme di tutte queste rette parallele fra di loro, come si esprime? Eccovi l’equazione del fascio di rette improprio.

La variabile qui è q! Quindi m assumerà sempre un certo valore preciso, ad esempio può essere m=2 o m=3 ecc.
Una retta può essere scritta sia in forma esplicita (come abbiamo fatto adesso, qui sopra), e sia in forma implicita (cioè con tutto a sinistra, a primo membro). Quindi, in tal caso, avremo una cosa del genere:
ax +by + k = 0\;\; con k \in \Reals
Dove k è il termine noto della forma implicita, unica variante.
Nell’esempio successivo, vediamo un piccolo caso particolare molto utile!
Esempio 4. Consideriamo un fascio improprio, con equazione y=3x + q . Che valore di q ha la rette che passa per l’origine?
Una retta che passa per l’origine è un qualcosa della forma seguente:
y=mx
Quindi per esempio y=2x o y=x o anche y=-2x. Di conseguenza se il nostro fascio è:
y=3x + q
Allora capiamo bene che, la retta associata al valore q=0…è proprio quelle che passa per l’origine! Di fatti otteniamo:
y=3x
Che passa per l’origine! Quindi, al valore q=0 del fascio di rette improprio, la retta associata a tale valore è quella che passa sempre per l’origine!
Fasci generati da due rette
Due rette, tramite la loro combinazione, possono generare un fascio di rette: proprio o improprio.
Consideriamo due rette r ed s in forma implicita:
r: \; ax+by+c=0
s: \; a'x+b'y+c'=0
I libri scrivono per comodità A(x,y)= ax+by+c, però questo potrebbe confondere, quindi noi non utilizzeremo questa notazione. Ma il senso è sempre lo stesso. Torniamo a noi.
Chiamiamo combinazione lineare delle rette r ed s, la seguente cosa:
p (ax+by+c) + q (a'x+b'y+c') \;\; con p,q \in \Reals
Nel nostro caso però abbiamo più precisamente che:
p (ax+by+c) + q (a'x+b'y+c')=0 \;\; con p,q \in \Reals
Perché la loro combinazione lineare fa 0? Tutto questo fa 0 perché le equazioni delle rette sono scritte in forma implicita, quindi fanno 0 anch’esse. Di fatti sostituendo otterremmo che:
p (0) + q (0) = 0 \;\; con p,q \in \Reals
Torniamo al discorso principale. Conoscendo le equazioni delle rette, allora le uniche variabili sono proprio q e p! Di fatti ad esempio potremmo avere:
p (x-2y+6) + q (3x+y+2) = 0
Questo rappresenta un fascio generato da due rette. Le rette r ed s sono dette generatrici, perché appunto generano tale fascio. Come è fatto questo fascio? E’ proprio o improprio? Lo vedremo fra poco.
Piccola curiosità:
Per chi volesse continuare gli studi all’Università, la combinazione lineare è un argomento molto caro alla geometria. Tal volta sarà più usuale vedere invece la combinazione lineare di vettori nell’algebra lineare. Ma il senso rimarrà lo stesso.
Fascio proprio generato da due rette
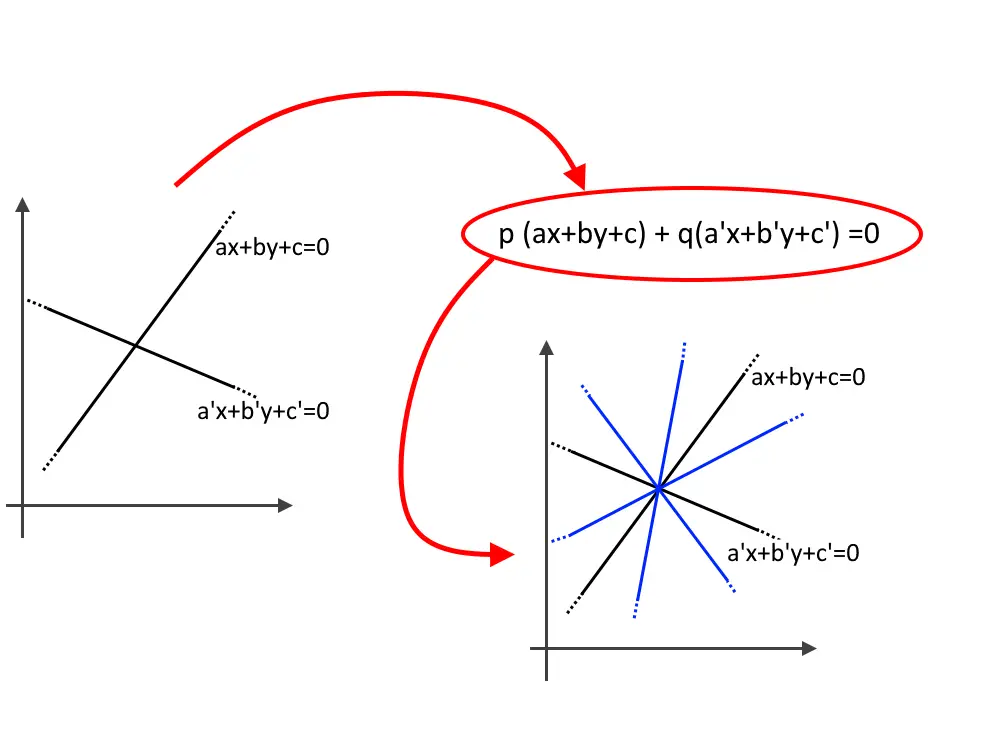
Abbiamo due rette r ed s. Queste due rette avranno una certa equazione, ad esempio:
r: \; x+2y+4=0
s: \; x-y+1=0
Queste due rette si intersecano in un punto. Se cliccate al di sopra vi è il procedimento su come trovare un punto di intersezione fra due rette.
Se due rette si intersecano in un punto, allora anche tutte le loro combinazioni lineari si intersecheranno in uno stesso punto: ossia il centro del fascio. Tale fascio sarà:
p (x+2y+4) + q (x-y+1) = 0 \;\; con q,p \in \Reals
Il fascio di rette è di conseguenza proprio, se le due rette generatrici si intersecano in un punto. Per capire se si intersecano basta verificare che:
\frac{a}{b} \ne \frac{a'}{b'}
Di fatti nel nostro caso, sostituendo i rispettivi valori, si ha:
\frac{1}{2} \ne \frac{1}{-1}
Che sono ovviamente diversi, e quindi si incontrano in un punto (centro del fascio). Tutto qui, facciamo un esempio subito!
Esempio 5. Consideriamo due rette di equazioni r: \; x+y+1=0 e la retta s: \; 3x+4y-5=0 . Il fascio generato da queste due rette è proprio? Che centro ha?
Il fascio generato dalle due rette r ed s è la loro combinazione lineare:
p (x+y+1) + q (3x+4y-5) = 0
Per dire se tale fascio è proprio (e quindi ha un centro) dobbiamo verificare che:
\frac{a}{b} \ne \frac{a'}{b'} \implies \frac{1}{1} \ne \frac{3}{4}
E sono chiaramente diversi valori, quindi il fascio è proprio. Che centro ha? Il centro è lo stesso punto di intersezione fra le due rette. Quindi ci calcoliamo il punto di intersezione delle due rette r ed s. Per far ciò mettiamo a sistema le due rette:
\begin{cases} x+y+1 = 0 \\ 3x+4y-5 = 0 \end{cases}
Un sistema di equazioni lo si può risolvere in diversi modi, noi usiamo quello per sostituzione:
\begin{cases} y = -x-1 \\ 3x+4y-5 = 0 \end{cases}
E poi sostituiamo la prima equazione nella y della seconda:
\begin{cases} y = -x-1 \\ 3x+4(-x-1)-5 = 0 \end{cases}
\begin{cases} y = -x-1 \\ 3x-4x-4-5 = 0 \end{cases}
E quindi ci ricaviamo la x:
\begin{cases} y = -x-1 \\ x = -9 \end{cases}
Poi sostituendo tale x nella prima equazione, troviamo anche la y. Questa x ed y sono le componenti del centro del fascio, che è lo stesso punto dell’intersezione fra le due rette.
\begin{cases} y = 8 \\ x = -9 \end{cases}
Il centro è per cui P=(-9,8)
Abbiamo detto che un fascio di rette, ha come equazione la combinazione lineare delle due rette generatrici:
p (ax+by+c) + q (a'x+b'y+c') = 0 \;\; con p,q \in \Reals
Supponendo p \ne 0 , possiamo dividere tutto per p:
ax+by+c + \frac{q}{p} (a'x+b'y+c') = 0 \;\; con p,q \in \Reals
Definendo k = \frac{q}{p} , allora la combinazione lineare o fascio di rette può anche essere scritto al variare della sola k:
ax+by+c + k (a'x+b'y+c') = 0 \;\; con k \in \Reals
Cos’ abbiamo un solo parametro piuttosto che due: è più semplice!
Fascio improprio generato da due rette
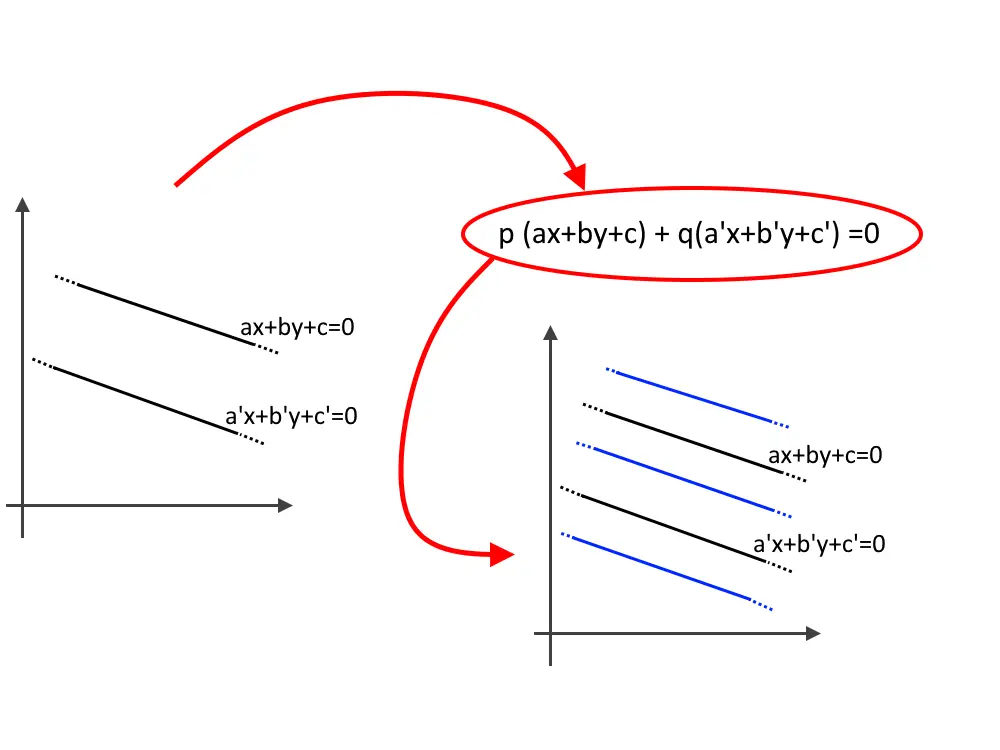
Analogamente al discorso fatto prima. Qui abbiamo due rette r ed s. Se tali rette sono parallele, allora la loro combinazione lineare produrrà un fascio improprio.
Per esempio abbiamo:
r: \; x+y-4=0
s: \; 3x+3y+1=0
Queste due rette sono parallele. Come facciamo a saperlo? Dobbiamo verificare la condizione di parallelismo fra due rette, quando sono in forma implicita:
\frac{a}{b} = \frac{a'}{b'} \implies \frac{1}{1} = \frac{3}{3}
E’ verificata tale condizione, quindi sono parallele. Di conseguenza la loro combinazione lineare:
p (x+y-4) + q (3x+3y+1) = 0 \;\; con p,q \in \Reals
Rappresenta un fascio improprio! Ossia di tante rette parallele! Di conseguenza anche qui non c’è un centro del fascio.
Possiamo fare un discorso analogo: supposto p \ne 0 si può scrivere il tutto al variare di un solo parametro:
x+y-4 + k (3x+3y+1) = 0 \;\; con k \in \Reals
Che ovviamente è molto più semplice, perché c’è solo un parametro! Ed useremo di fatti questa forma negli esercizi!
Esempio 6. Sia il fascio di equazione -x-y-2 + k (3x+3y) = 0, è improprio? Che centro ha?
Per verificare se il fascio generato da due rette è improprio, dobbiamo verificare l’uguaglianza di:
\frac{a}{b} = \frac{a'}{b'} \implies \frac{-1}{-1} = \frac{3}{3} \implies 1=1
L’uguaglianza c’è: il fascio è improprio. Cioè ci saranno un insieme infinito di rette parallele.
Che centro ha? Un fascio improprio non ha centro.
Per esercizi svolti sul fascio di rette cliccare qui.
La pagina è conclusa, speriamo sia stato chiaro tutto. Trovate altri centinaia di argomenti ed esercizi svolti sia di matematica che di geometria analitica e geometria!
Continuate a supportarci!
punto
intersezione
rette
esercizi