Direttrice parabola: formula, equazione e come calcolarla
In questa pagina vedremo che cos’è la direttrice di una parabola e come trovarla. Il calcolo della direttrice è uno dei vari step per poter disegnare una parabola. Inoltre la sua equazione è presente in molti esercizi inerenti alla parabola, quindi cominciamo subito a vedere che cos’è e come trovarla!
Indice
Ogni parabola ha la sua direttrice, e noi la rappresentiamo sempre con una equazione. L’equazione della direttrice rappresenta una retta nel piano cartesiano. Vediamo come trovarla e le formula da usare per ogni caso. Iniziamo!
Formula direttrice parabola
Distinguiamo diverse tipologie di parabole. Ognuna ha la sua equazione. In questa sezione le vedremo una per volta.
Retta direttrice della parabola con vertice in origine ed asse coincidente all’asse y
Non spaventiamoci della lunghezza del titolo. In pratica, come dice la frase stessa, siamo nel caso di una parabola che ha il vertice in V=(0,0), e poi ha l’asse che è proprio l’asse y! L’equazione di questo tipo di parabola è della forma:
y=ax^2
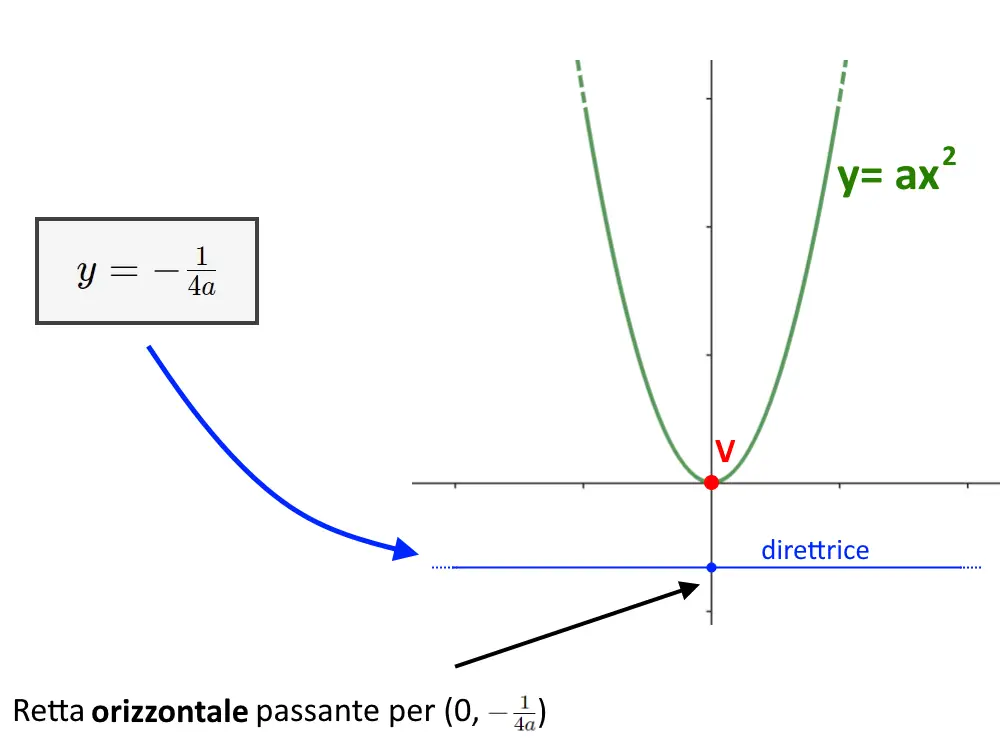
Dove è posizionata la direttrice? In questo caso la direttrice è disposta in orizzontale, nel punto dato dalla seguente formula:
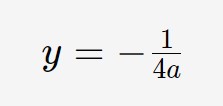
Il posizionamento della direttrice dipende quindi dal valore del coefficiente a. Di fatti a seconda del fatto che a sia negativo o positivo, il segno dell’equazione della direttrice cambia. Questo causa un diverso posizionamento della direttrice. Ad esempio se a>0 la direttrice è disposta al di sotto della parabola, se a<0 invece sta al di sopra della parabola.
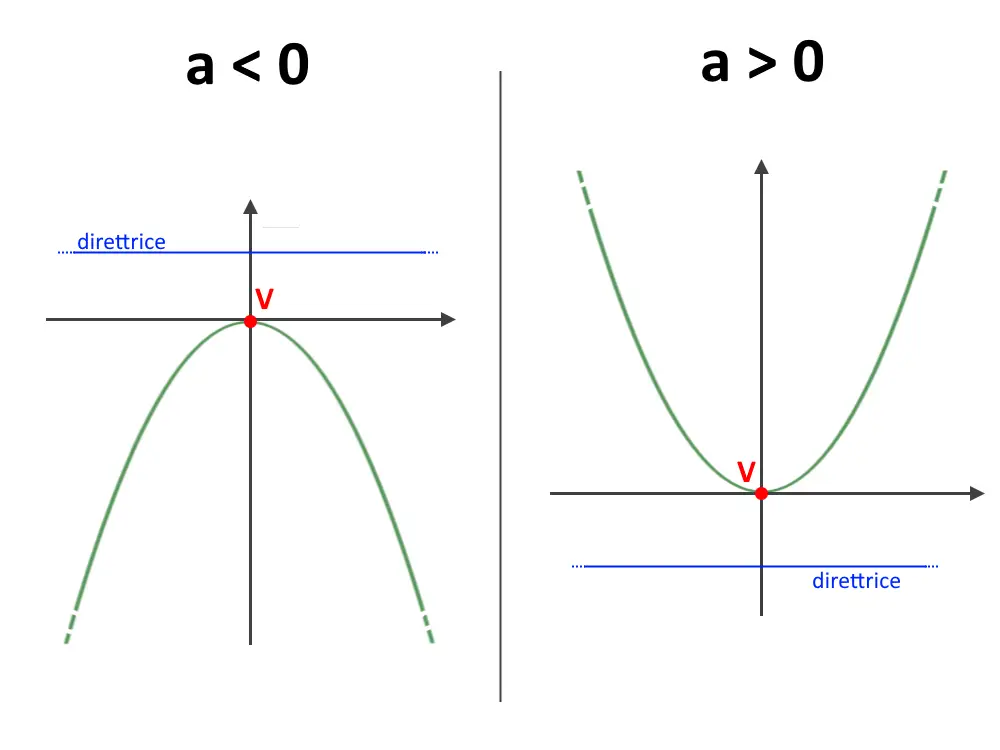
Non serve imparare questo a memoria: semplicemente la direttrice sta verso dove è posizionato il vertice!
Passiamo alla prossima tipologia di parabola. Con questa abbiamo concluso: alla fine della pagina ci saranno esempi pratici di come calcolarla.
Retta direttrice della parabola con asse parallelo all’asse y
La frase del titolo è più semplice: abbiamo una parabola che ha l’asse verticale. Quindi vertice è variabile ed anche disposizione spaziale. L’equazione è della forma:
y=ax^2 +bx + c
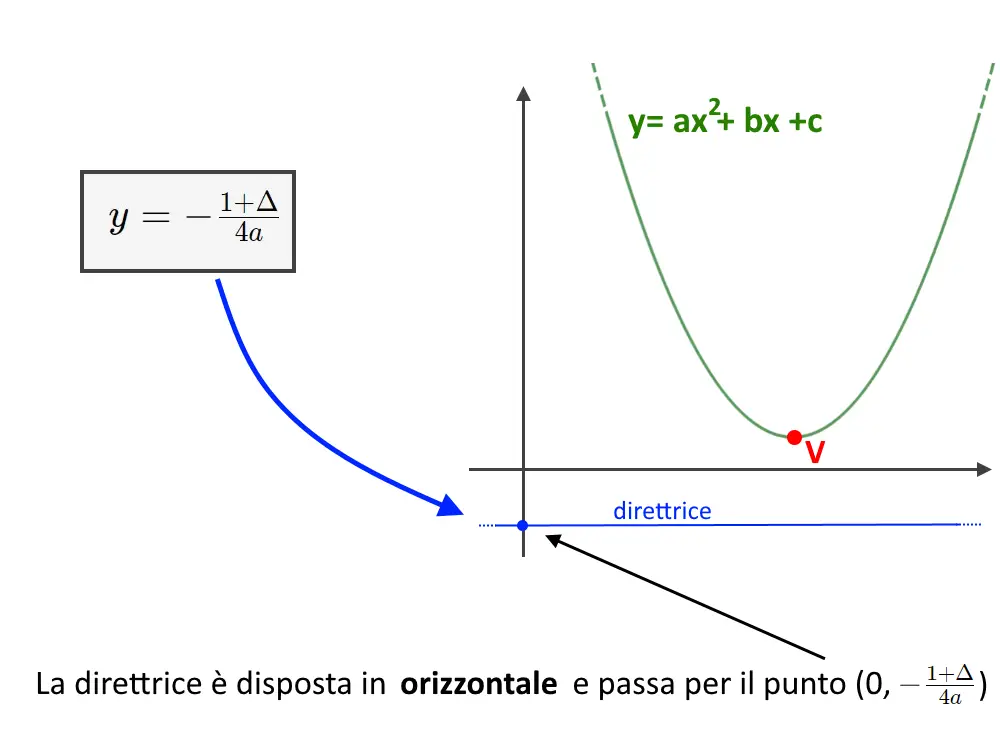
La direttrice di questa parabola è sempre disposta in orizzontale, ed è data dalla seguente formula:

Come possiamo notare dalla formula, il segno ed il valore della direttrice dipendono dal valore dei coefficienti a e \Delta.
Analogamente a prima, anche qui abbiamo che se a>0 la direttrice è disposta al di sotto della parabola, se a<0 invece sta al di sopra della parabola.
Curiosità. Perché il segno dei coefficienti b e c non influenzano questa caratteristica? Beh, questa è una cosa che si fa al quinto anno di Liceo. Ma per farla breve: il termine quadratico x^2 è molto più forte degli altri, e quindi lui domina. Di conseguenza la disposizione verso l’alto o verso il basso è solo data da lui.
Curiosità. Se notate y=ax^2 +bx +c ha il membro di destra che è proprio una classica equazione di secondo grado, e non a caso compare proprio il delta \Delta = b^2 -4ac !
Passiamo all’ultimo tipo di parabola adesso!
Retta direttrice della parabola con asse parallelo all’asse x
Qui abbiamo una parabola disposta in orizzontale invece. Il suo asse è parallelo all’asse x adesso. La sua equazione è data dallo scambiare la x con la y in pratica:
x = ay^2 + by +c
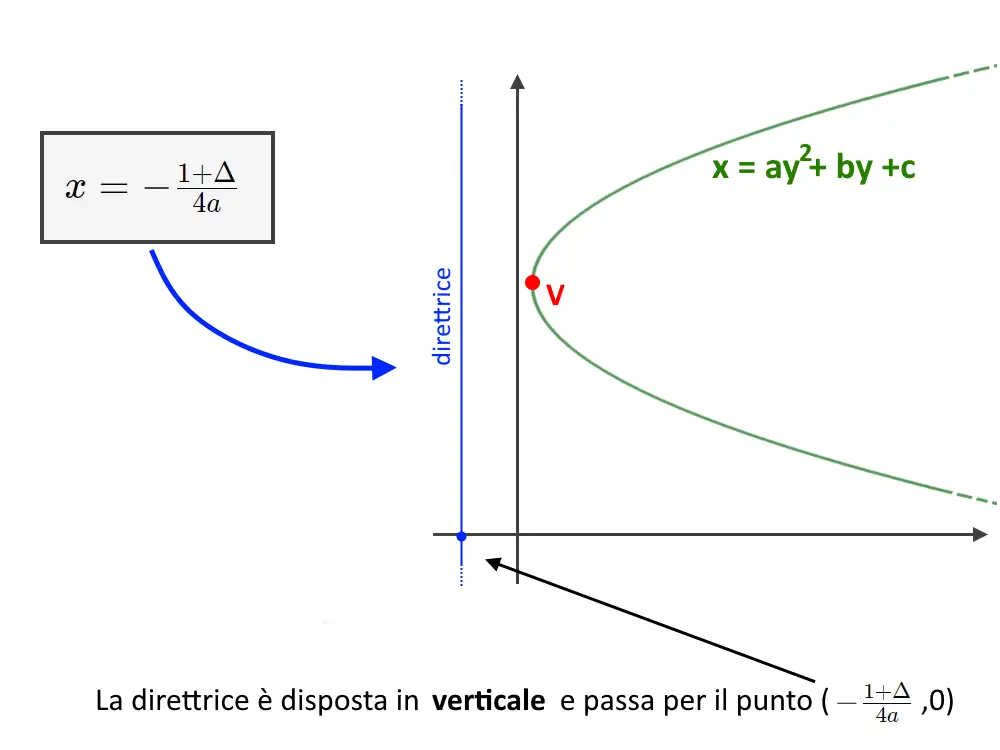
Questa volta la direttrice è disposta in verticale! Questo per ragioni di definizione della parabola stessa, ragioni dette all’inizio della pagina. La retta segue ora questa formula:

Notiamo che è la stessa identica formula di prima, basta solo invertire x con la y: questo è un modo per ricordarsela!
Anche qui al variare del segno del coefficiente a possiamo avere differenti disposizioni della retta direttrice. Di fatti, se a>0 la direttrice sta sulla sinistra, se a<0 sta sulla destra invece.
Come nella curiosità della sezione precedente, anche qui vale lo stesso discorso (argomento di quinto Liceo). Cioè è il termine quadratico che comanda, di conseguenza solamente il coefficiente a ne determina la “direzione” della parabola.
Curiosità. Questa parabola non è una funzione, di fatti ad ogni x del dominio vi corrispondono più di una y.
Adesso è giunto il momento di vedere degli esempi di come calcolare la direttrice, come trovarla e come disegnarla! Vediamo quindi degli esercizi svolti!
Come calcolare la direttrice: ESEMPI
Di seguito riassunto il procedimento mentale che bisogna fare quando si ha a che fare con il calcolo di una direttrice.
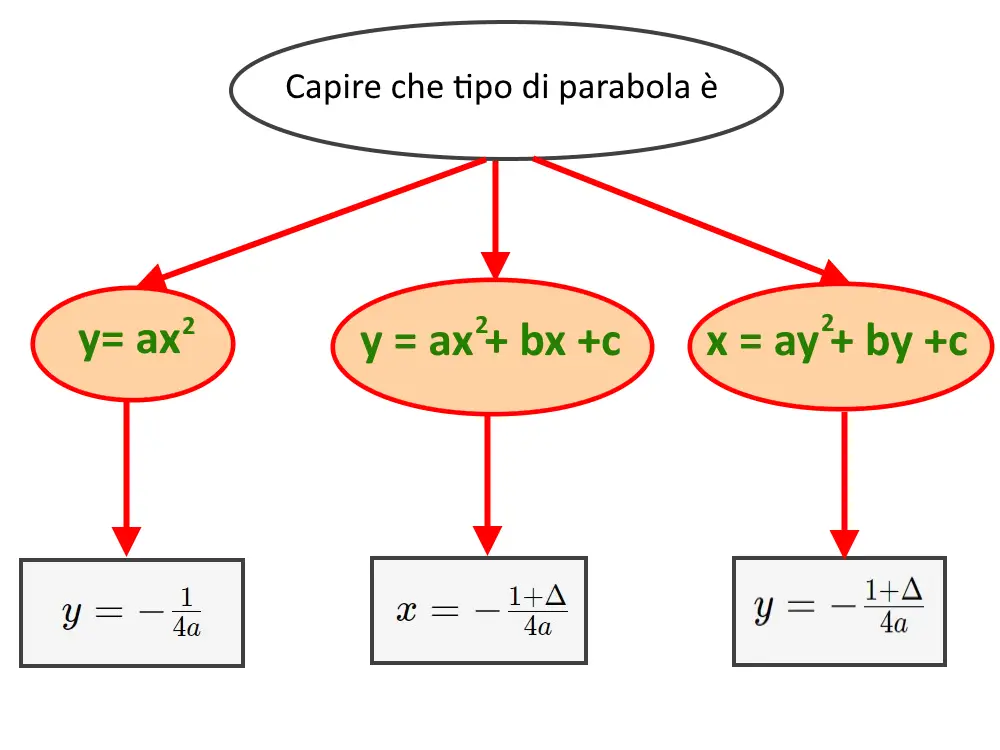
Esempio 1. Calcolare la direttrice della parabola avente equazione y=4x^2 .
Osserviamo l’equazione: è sicuramente di una parabola della forma y=ax^2 . Di conseguenza, per calcolare la direttrice, dobbiamo usare la formula:
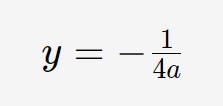
Quindi ci serve il valore di a. Dal confronto dell’equazione dell’esercizio con quella generale capiamo chi è il coefficiente a:
y=ax^2
y=4x^2
Capiamo quindi facilmente che a=4. Sostituiamo nella formula della direttrice tale valore:
y = - \frac{1}{4 \cdotp 4} = - \frac{1}{16}
Esempio 2. Trovare e disegnare la direttrice della parabola avente equazione y=x^2 -2x+1 .
Guardiamo la traccia dell’esercizio e capiamo che essa è una parabola del tipo generale:
y = ax^2 +bx +c
La formula da usare è quindi:

Ci servono il coefficiente a e \Delta . Dal confronto:
y = ax^2 +bx +c
y=x^2 -2x+1
Capiamo che:
\begin{cases} a=1 \\ b= -2 \\ c=1 \end{cases}
Mentre il \Delta = b^2 - 4ac = (-2)^2 - 4 \cdotp 1 \cdotp 1 = 4-4=0
Sostituiamo tutto ciò che ci serve nella formula della direttrice della parabola:
y = - \frac{1+ \Delta }{4a} = - \frac{1+ 0 }{4 \cdotp 1} = - \frac{1}{4}
L’esercizio ci chiede anche disegnarla. Come sappiamo questa è disposta in orizzontale. Quindi partiamo dal punto di ordinata y= - \frac{1}{4} , per la precisione dal punto (0,- \frac{1}{4}) e poi tracciamo una retta orizzontale passante per questo punto.
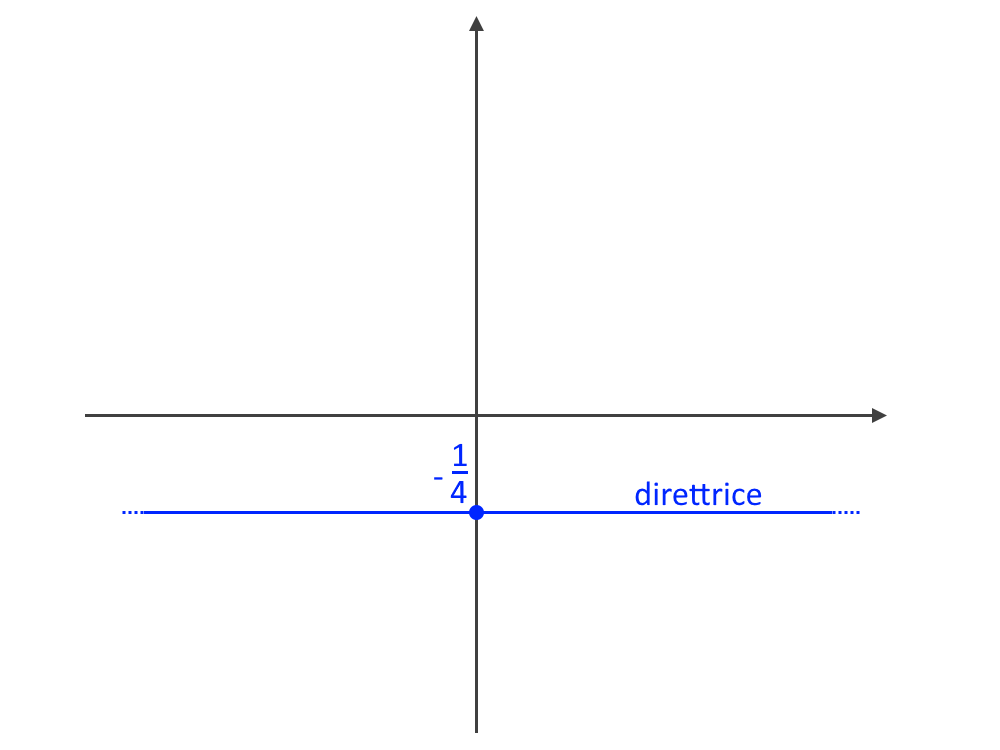
Ed ecco fatto!
Esempio 3. Determinare l’equazione della parabola avente direttrice x=4 , sapendo inoltre che b=0 e c=0.
Dal fatto che la direttrice presenta una retta del tipo x=cost. allora capiamo che ci troviamo nell’ultimo caso, ossia parabola con asse parallelo ad x:
x = ay^2 +by + c
Il problema ci dice anche che b=0 e che c=0, quindi l’equazione diventa:
x = ay^2
Dobbiamo solo calcolarci la a. Tale coefficiente possiamo trovarlo dall’informazione della direttrice. Sappiamo che una direttrice di questo tipo presenta la formula:
x = \frac{1+ \Delta }{4a}
Ma sappiamo che essa vale x=4, quindi:
\frac{1+ \Delta }{4a} = 4
Il delta in realtà possiamo trovarcelo, di fatti sarebbe:
\Delta = b^2 - 4ac = 0^2 - 4 \cdotp a \cdotp 0 = 0-0 = 0
E quindi l’equazione di prima diventa:
\frac{1}{4a} = 4
Ora dobbiamo solo risolverla! Moltiplichiamo per 4a per eliminare la frazione:
1 = 4 \cdotp 4a
1 = 16a \implies a = \frac{1}{16}
E quindi l’equazione della parabola è:
x = \frac{1}{16}y^2
Per altri esercizi sulla parabola clicca qui.
La pagina è conclusa, speriamo sia stato chiaro tutto. Nel nostro sito abbiamo poi altri centinaia di argomenti e pagine di esercizi svolti di Matematica, Geometria Analitica e Geometria!
Continuate a supportare il nostro sito!
parabola
esercizi