Equazioni differenziali lineari primo ordine: FORMULE & ESEMPI
Le equazioni differenziali del primo ordine sono l’ultimo argomento del Liceo, e molto spesso citate ed usate in Università. Questa pagina è adatta quindi a queste due figure di studenti. Qui vedremo formule, esempi svolti, esercizi risolti e tanti consigli per riuscire a trovarsi sempre con la soluzione del libro! Inizieremo con un primo paragrafo che spiega come riconoscere una equazione differenziale lineare del primo ordine; e poi distingueremo due casi.
Indice
- Come riconoscere una equazione differenziale del primo ordine
- CASO 1: Equazione differenziale omogenea
- CASO 2: Equazione differenziale completa
Fatta questa piccola introduzione, immergiamoci nelle equazioni differenziali, concentrandoci su cosa vuol dire primo ordine, e come risolverle.
Come riconoscere una equazione differenziale lineare del PRIMO ORDINE
Partiamo subito dritti al punto: una equazione differenziale lineare è un qualcosa di questo tipo.
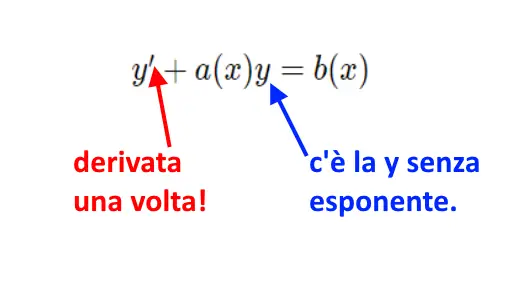
Differenziale vuol dire che compare la derivata y’.
Sul “lineare” non c’è molto bisogno di concentrarci, se si è al Liceo. Se invece volete approfondire questo aspetto cliccate qui.
Invece, del primo ordine significa due cose:
- La derivata è y’ (ipsilon primo), cioè la funzione y derivata una volta
- L’altra y che compare ha come esponente 1.
Sulla x invece non ci sono limitazioni, possono essere come vogliono. Vediamo alcuni esempi di equazioni differenziali del primo ordine.
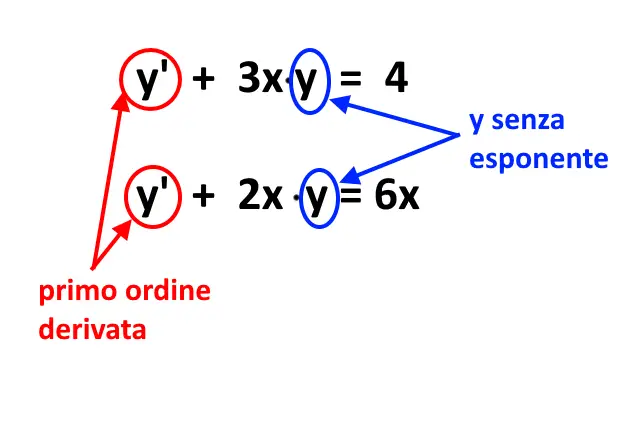
Ora che abbiamo capito come riconoscere una equazione differenziale del primo ordine, vediamo invece alcuni esempi di equazioni differenziali che non sono del primo ordine!
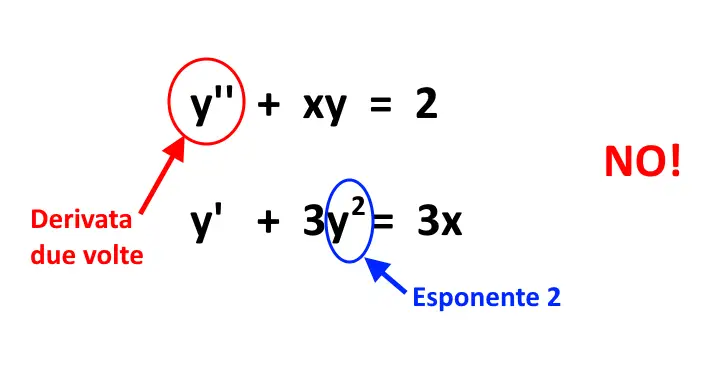
Adesso siamo in grado di comprendere le formule per risolvere queste equazioni differenziali! Dobbiamo distinguere due diversi casi:
- Equazioni differenziali omogenee
- Equazioni differenziali complete
CASO 1: Equazione differenziale del primo ordine OMOGENEA
Abbiamo detto che stiamo considerando una generica seguente equazione differenziale del primo ordine:
y' +a(x)y = b(x)
Omogenea significa semplicemente che b(x)=0. Cioè quindi:
y' +a(x)y = 0
Di conseguenza l’equazione è in questo caso la seguente, con la formula risolutiva:

Prima di vedere alcuni esercizi svolti usando questa formula, per chi si ricorda un po’ le equazioni differenziali a variabili separabili, avrà notato che questa equazione è proprio a variabili separabili! E di fatti la formula finale viene fuori proprio dal risolvere questa come una equazione differenziale a variabili separabili!
Quindi, se non vi ricordate la formula, basta che vi ricordate il procedimento delle equazioni differenziali a variabili separabili, è proprio lo stesso! Quindi, per chi è interessato, andiamo a dimostrare tale formula:
y' +a(x)y = 0
y' = - a(x)y
Poi, ricordando il significato di y’:
\frac{dy}{dx} = - a(x)y
Essendo a variabili separabili, portiamo tutte le y a sinistra, e le x a destra:
\frac{dy}{y} = - a(x)dx
Integriamo ambo i membri:
\int \frac{dy}{y} = - \int a(x)dx
Il primo integrale, ricordando nella tabella degli integrali, ha come risultato un logaritmo. Il secondo integrale, non sapendo come è fatto a(x) lo lasciamo così com’è, esso dipenderà dall’esercizio.
\ln |y| +c = - \int a(x)dx
\ln |y| = -c - \int a(x)dx
L’obiettivo di queste equazioni è quello di trovare la y, quindi usiamo la formula di risoluzione delle equazioni logaritmiche (poiché y sta dentro un logaritmo ora).
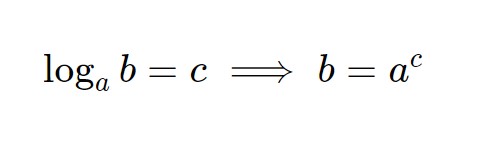
|y| = e^{-c- \int a(x)dx }
Per la proprietà delle potenze:
|y| = e^{-c} e^{- \int a(x)dx }
Essendo che quando si risolve questa equazione differenziale, si considera la x come un numero, poiché vogliamo solo la y, questa sarebbe del tipo:
|y| = w \implies y = \pm w
Quindi otteniamo così finalmente:
y =\pm e^{-c} e^{- \int a(x)dx }
Chiamiamo \pm e^{-c} = k una certa costante generica arbitraria, visto che c dall’integrazione è arbitraria, ed otteniamo così:
y = k e^{- \int a(x)dx }
Ora che abbiamo capito quale formula usare, e come si dimostra, veniamo a qualche esempio svolto!
Esempio 1. y' + 3xy = 0
Prima di partire col botto con l’utilizzo della formula, bisogna sempre chiedersi se è questo il caso dell’equazione differenziale del primo ordine, omogenea. Ed effettivamente sì lo è. Questo ve lo dico perché nella verifica in classe ci saranno tutti i tipi di equazioni differenziali, quindi è buona abitudine che vi facciate prima questa domanda. L’equazione è quindi omogenea, ossia del tipo:
y' +a(x)y = 0
Quindi nel nostro caso, la funzione a(x)=3x. Capito questo, dobbiamo quindi usare la formula seguente:
y = k e^{- \int a(x)dx }
Sostituiamo la parte a(x) chiaramente:
y = k e^{- \int 3x \; dx }
L’esercizio si conclude andando a risolvere solo l’integrale, tutto qui. Quindi dobbiamo calcolare esplicitamente l’integrale che compare:
\int 3x \; dx = 3 \frac{x^2}{2}
E mettiamo questo valore al posto dell’integrale:
y = k e^{- 3 \frac{x^2}{2} }
L’esercizio è finito, abbiamo trovato la y. Quindi, nel caso delle equazioni differenziali del primo ordine omogenee, si tratta alla fine di calcolare un integrale!
Esempio 2. y' = \frac{1}{x} y
Questo esercizio è utile, poiché vedremo un paio di cose che potranno servirvi! Partiamo col presupposto che sembra una equazione del tipo omogenea, quindi vogliamo ricondurci a:
y' +a(x)y = 0
Vogliamo capire nel nostro caso chi è a(x). Quindi portiamo tutto a primo membro:
y' - \frac{1}{x} y = 0
Vediamo che c’è un segno meno, invece di un più, quindi nel nostro caso a(x)=- \frac{1}{x} , poiché:
y' + (- \frac{1}{x}) y = 0
Fatto ciò dobbiamo usare la formula risolutiva:
y = k e^{- \int a(x)dx }
Dobbiamo quindi risolvere solo l’integrale.
\int - \frac{1}{x} dx = - \ln |x|
Sostituiamo nella formula, e noteremo una cosa:
y = k e^{- (- \ln |x|) } = k e^{ \ln |x| }
A questo punto siamo giunti al risultato, però ci possiamo ricordare una proprietà molto utile dell’esponenziale e del logaritmo, che in questi esercizi viene fuori abbastanza spesso:
e^{\ln a } = a
Quindi il risultato è molto più semplice e scritto compatto:
y = k |x|
Fatti questi due esempi, più che sufficienti a capire come si risolvono le equazioni differenziali nel caso omogeneo, passiamo al prossimo caso!
CASO 2: Equazione differenziale del primo ordine COMPLETA
Se nel caso omogeneo ponevamo la funzione b(x)=0, qui invece l’equazione differenziale si dice del primo ordine completa, poiché ha anche b(x)! Senza vedere la lunghetta dimostrazione per ricavare la formula finale, passiamo subito al sodo.

Anche in questo caso si tratta solo di risolvere degli integrali, in questo caso dovremo andare a calcolare precisamente sempre due integrali. Vediamo dunque degli esempi subito.
Esempio 1. y' + \frac{y}{x} - x = 0
Essendo y’ e la y con esponente 1, sembra proprio essere una equazione diff. del primo ordine completa, quindi dobbiamo ricondurci innanzitutto a questa forma seguente, per capire chi sono a(x) e b(x):
y' +a(x)y = b(x)
Allora portiamo la x a destra, e poi riscriviamo:
y' + \frac{1}{x}y = x
Scrivendola in questo modo, non abbiamo difficoltà a capire che a(x)= \frac{1}{x} e che b(x)=x!
L’equazione ha come soluzione la formula citata già in precedenza:
y= e^{-\int a(x)dx } [ \int b(x) e^{\int a(x)dx} dx +c ]
Il primo integrale che notiamo, per ben due volte è (vi consiglio sempre di iniziare da questo):
\int a(x)dx = \int \frac{1}{x} dx = \ln |x|
Fatto questo, passiamo all’integrale:
\int b(x) e^{\int a(x)dx} dx
Dove ovviamente andiamo a sostituire quello all’esponente già calcolato!
\int x e^{\ln |x|} dx
Sfruttando la proprietà molto utile dei logaritmi, che serve tantissime volte in questi esercizi:
e^{\ln a } = a
Quindi otteniamo un integrale molto più semplice da risolvere:
\int x \cdotp |x| dx
Supponiamo che x>0 (per via del fatto che la x sta dentro il logaritmo, per il dominio del logaritmo, possiamo assumere che x>0 e quindi levare il valore assoluto):
\int x\cdotp x dx = \int x^2 dx = \frac{x^3}{3}
Sostituiamo tutto nella formula, abbiamo i due integrali quindi andiamo a finire l’esercizio:
y= e^{-\ln x} [ \frac{x^3}{3} +c ] = e^{\ln x^{-1} } [ \frac{x^3}{3} +c ] = \frac{1}{x}[ \frac{x^3}{3} +c ]
La pagina è conclusa. Speriamo sia tutto stato chiaro. Nel caso aveste dei dubbi ci potete contattare per email! Risponderemo in men che non si dica, e nel caso segnalateci eventuali errori, grazie!