Equazioni differenziali a variabili separabili: ESERCIZI SVOLTI

In questa pagina vedremo come risolvere le equazioni differenziali, a variabili separabili. Forniremo tantissimi esempi ed esercizi svolti. Questa pagina fungerà da guida per voi, studiate e prendete appunti qui, e non avrete bisogno di girovagare in internet!

Indice

• Quando abbiamo una equazione differenziale a variabili separabili?
• Esercizi svolti
• Domande frequenti

Detto questo, andiamo subito al sodo. Vediamo innanzitutto quando siamo di fronte ad una equazione differenziale a variabili separabili.

---

Quando abbiamo una equazione differenziale a variabili separabili?

Abbiamo una equazione differenziale a variabili separabili (come mostra l’esempio seguente), quando si hanno due cose:

• Presenza della derivata y’
• Possibilità di separare le variabili x ed y tramite una moltiplicazione

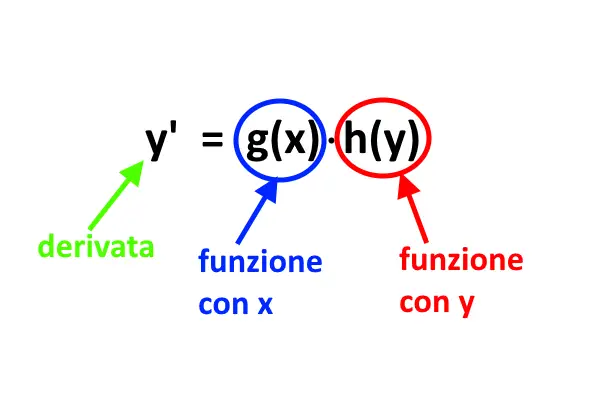
Come mostra l’esempio di sopra, abbiamo a sinistra la presenza di y’, che ci fa capire che siamo di fronte ad una equazione differenziale.

Poi a destra, abbiamo la parte con la x, e la parte con la y SEPARATE.

Cosa vuol dire separate? Variabili separate vuol dire che riusciamo a mettere la x e la y distaccate, per mezzo di una moltiplicazione fra le due funzioni che contengono x e y.

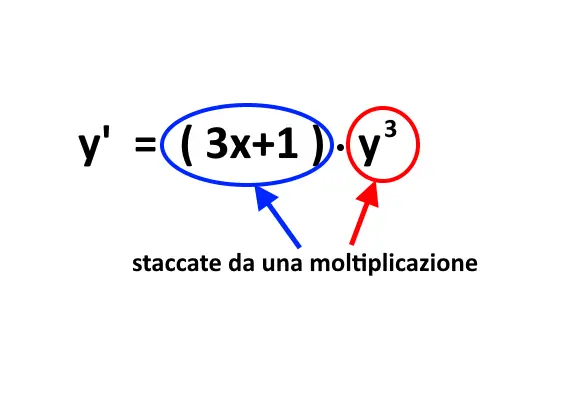
Quando invece non sono separate? NON sono separate nei seguenti esempi. Nel primo esempio notiamo che x ed y sono distaccate da una somma, e non va bene. Ricordiamo che si dicono separate solo quando lo sono per mezzo di una moltiplicazione.

Nel secondo esempio invece, qualsiasi formuletta usassimo, non arriveremmo mai ad avere una forma di equazione differenziale a variabili separabili, e quindi non lo sono.

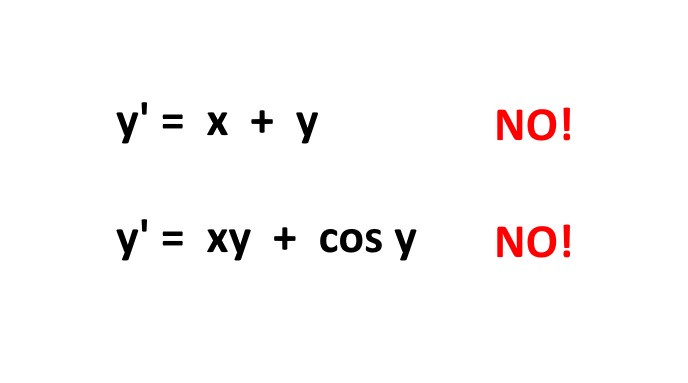
Come faccio quando non sembrano subito separabili? Capita spesso di avere un esercizio del tipo: \frac{ y' }{x} = 1+ y^2 in cui effettivamente non sembra il nostro caso che stiamo trattando. Invece bisogna un attimo osservare meglio l’equazione, per capire se possiamo fare qualcosa.

Prima di mollare, dobbiamo quindi provare ad agire: in questo caso basta moltiplicare tutto per x, per accorgerci di essere proprio nel caso della variabili separabili!

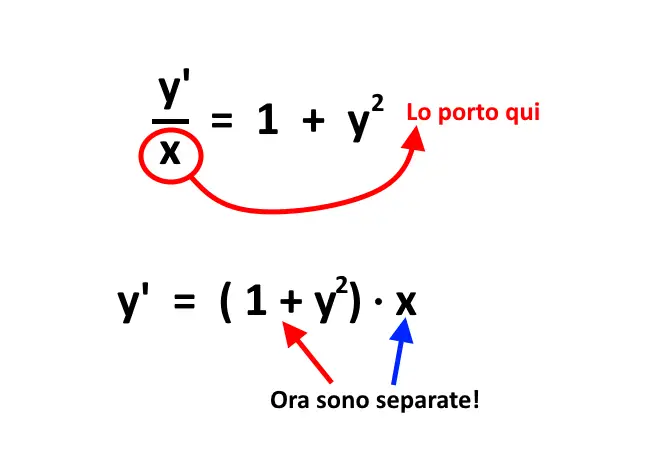
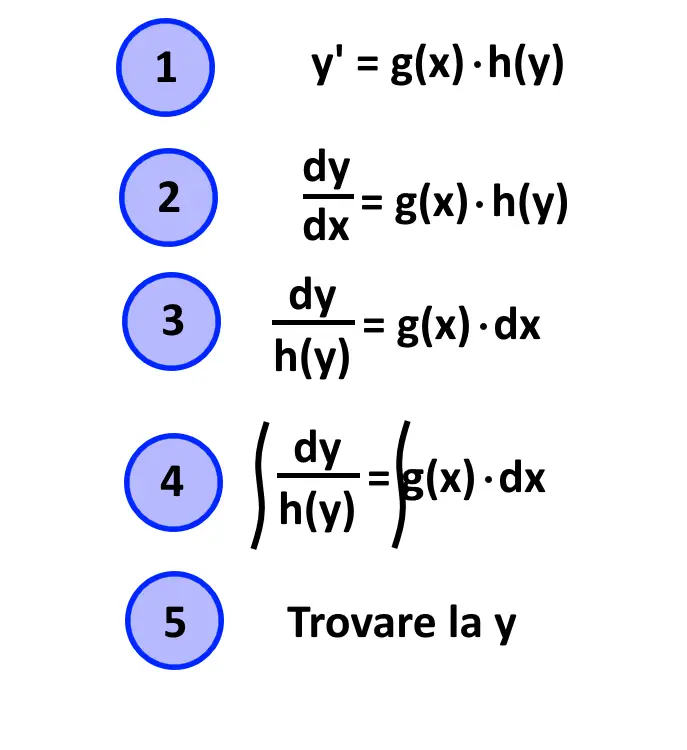
E poi come si risolve? Bisogna trovare la y. Allora, ricordiamo innanzitutto che: y' = \frac{dy}{dx} . Poi portiamo la parte con la y a sinistra, e il dx a destra.

Isoliamo quindi tutte le y a sinistra, e tutte le x a destra. Dopo di che si integra.

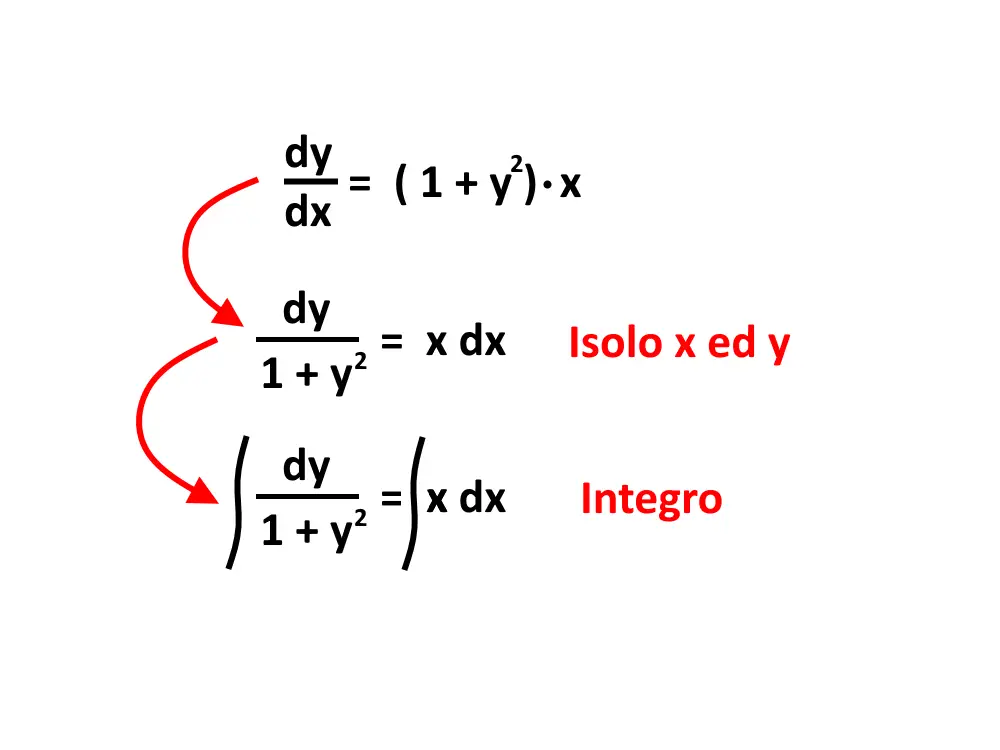
A questo punto non ci resta che trovare la y.

Ora che abbiamo quindi capito in linea generale cosa è una equazione differenziale, a variabili separabili, e come si risolvono, vediamo degli esercizi svolti e spiegati passo dopo passo!

Come si risolvono le equazioni differenziali a variabili separabili: ESERCIZI SVOLTI

Riassumiamo quindi i passaggi generali che dobbiamo seguire, per risolvere gli esercizi. C’è anche un ulteriore passaggio, che capita quasi sempre, che vi faremo vedere però dal terzo esercizio.

Esercizio 1. y' = x( 1+ y^2 )


L’equazione differenziale che ci ritroviamo in questo esercizio, è a variabili separabili. Notiamo infatti che la parte con la x e la parte con la y sono separate da una moltiplicazione.

Passiamo dunque al punto successivo: ricordiamoci di scrivere y’ come \frac{dy}{dx} .

\frac{dy}{dx} = x( 1+ y^2 )

Terzo punto: portiamo la y a sinistra, e poi la x a destra. Dividiamo tutto per 1+y^2:

\frac{dy}{dx} \frac{ 1 }{1+ y^2} = x

Moltiplichiamo per dx ed il gioco è fatto:

\frac{ dy }{1+ y^2} = x dx

Siamo giunti al quarto punto: quello di integrare tutto, e di risolvere gli integrali che compaiono.

\int \frac{ dy }{1+ y^2} = \int x dx

Ed ora si tratta di risolvere gli integrali, uno per volta, indipendentemente. Se non vi ricordate come si risolvono, date una ripassata qua. Guardando nella tabella degli integrali, possiamo risolvere immediatamente sia il primo che il secondo.

\arctan y = \frac{x^2}{2} +c

Risolti gli integrali, non ci rimane che trovare la y. In questo ultimo passaggio, dobbiamo trattare la x come se fosse una costante. Non dobbiamo pensarla quindi. Pensiamo solo alla y.

In questo caso basta applicare la funzione inversa dell’arcotangente, per trovare la y:

y = \tan ( \frac{x^2}{2} +c )

I giochi sono fatti! Non sono esercizi cortissimi. Bisogna quindi fare un punto alla volta, senza fretta. Meglio fare pochi esercizi fatti bene, e capirli, piuttosto che provare a farne dieci. Fatene giusto due o tre, in un paio di giorni e capirete come si fanno senza problemi.

RICORDA: quando integrate mettete una sola “c”!

Esercizio 2. y' = e^{-x+y}


In questo caso l’equazione non sembra fin da subito della forma del primo punto, quindi dobbiamo prima agire noi in qualche modo. Sfruttando la proprietà delle potenze, secondo la quale:

a^{b+c} = a^b \cdotp a^c

Allora, nel nostro caso possiamo separare le due variabili, tramite una moltiplicazione fra le due funzioni esponenziali:

y' = e^{-x} e^y

Siamo riusciti ad avere una forma del primo punto del nostro elenco. Quindi possiamo passare a riscrivere la y’:

\frac{dy}{dx} = e^{-x} e^y

E poi portiamo la parte con la y a sinistra, e il solito dx a destra (questo passaggio sempre):

\frac{dy}{e^y} = e^{-x} dx

Integriamo ambo i membri:

\int \frac{dy}{e^y} = \int e^{-x} dx

Per risolvere il primo integrale basta portare l’esponenziale sopra, aggiungendo un segno meno all’esponente:

\int e^{-y} dy = \int e^{-x} dx

Guardando come sempre nella tabella degli integrali immediati, ci accorgiamo che ci serve un segno meno dentro ai due integrali, e allora mettiamo due segni meno. Questo perché dentro all’integrale ci serve la derivata di “-y”. Questo vale anche per “-x”. Ricordando che meno per meno fa più, non cambiamo il valore dell’espressione, e quindi possiamo farlo.

- \int - e^{-y} dy = - \int - e^{-x} dx

- e^{-y} = - e^{-x} +c

Cambiamo tutto di segno:

e^{-y} = e^{-x} - c

Una costante la possiamo denominare col segno che vogliamo, poiché è arbitraria. Dunque la possiamo anche mettere col segno positivo per comodità:

e^{-y} = e^{-x} + c

Non dimentichiamoci mai il nostro obiettivo: trovare la y. In questo passaggio trattiamo la x come se fosse un numero semplice, quindi è come se ci trovassimo di fronte ad una equazione esponenziale. Queste si risolvono sfruttando la relazione seguente.

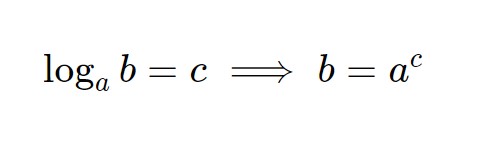
Chiaramente guardiamola al contrario. Nel nostro caso dunque, sarà:

-y = \ln ( e^{-x} +c )

Cambiamo di segno ed i giochi sono fatti:

y = - \ln ( e^{-x} +c )

L’esercizio è dunque concluso. Se il professore vi dice che vuole anche che semplifichiate il risultato in una forma migliore, allora ecco a voi ulteriori passaggi aggiuntivi (l’esercizio è concluso e vi trovate, sono passaggi giusto per). Riscriviamo l’esponenziale:

y = - \ln ( \frac{1}{e^x} +c )

Facciamo il minimo comune multiplo:

y = - \ln ( \frac{e^x +ce^x}{e^x} )

Dopo di che, ricordando che un segno meno davanti ad un logaritmo equivale a:

y = \ln ( \frac{e^x +ce^x}{e^x} )^{-1}

y = \ln ( \frac{e^x}{e^x +ce^x} )

Esercizio 3. y' = (4x+1)y

Gli esercizi visti fino ad ora hanno sempre trattato il caso in cui h(y) era diverso da zero sempre, e quindi non ci dava problemi. Da ora in poi vedremo alcuni casi in cui questo ci farà fare un passaggio in più, e ci farà ottenere un risultato in più.

Non spaventatevi: i passaggi sono gli stessi, ce n’è solo uno in più che vi faremo vedere con calma.

L’equazione differenziale è a variabili separabili, e quindi riscriviamo subito:

\frac{dy}{dx} = (4x+1)y

Portiamo la y a sinistra, MA nel fare questo dividiamo per y. E ciò significa che, per il dominio di una frazione, segue che deve essere y \ne 0 per andare avanti. Dobbiamo supporre inizialmente che y \ne 0 . Fatto ciò continuiamo, come se non fosse successo nulla. Il passaggio aggiuntivo ci sarà alla fine! Quindi scriviamo:

\frac{dy}{y} = (4x+1)dx

\int \frac{dy}{y} = \int (4x+1)dx

Per la risoluzione, spezziamo il secondo integrale in due più facili:

\int \frac{dy}{y} = \int 4x \;dx+ \int dx

Svolgiamo gli integrali, otteniamo:

\ln |y| = \frac{4x^2}{2} + x+c

\ln |y| = 2x^2+ x+c

Dobbiamo trovare la y. Siamo di fronte ad una equazione logaritmica. Allo stesso modo di quella esponenziale, dobbiamo usare la seguente formula.

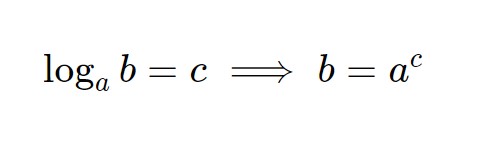
Dunque:

|y| = e^{2x^2+ x+c}

Ricordiamo che la x alla fine la trattiamo come un numero, di conseguenza abbiamo come se fosse:

|y| = k \implies y = \pm k

Segue che:

y = \pm e^{2x^2+ x+c}

E fino a qui non cambia nulla, come abbiamo detto. C’è però il passaggio aggiuntivo adesso! Abbiamo in pratica supposto che y \ne 0 . Tale passaggio aggiuntivo consiste nel vedere cosa succede se y=0!

PASSAGGIO AGGIUNTIVO: ciò che dobbiamo fare è sostituire semplicemente il valore di y=0 dentro la traccia dell’esercizio, e verificare che l’equazione sia soddisfatta: ossia verificare che, con y=0, allora anche y’=0. Se ciò accade, allora significa che anche y=0 è soluzione.

y' = (4x+1)y

y' = (4x+1) \cdotp 0

y' = 0

Abbiamo verificato la equazione differenziale, in questo caso particolare. Concludiamo che anche y=0 è soluzione insieme all’altra!

Esercizio 4. y' = \frac{\cos x}{\cos y}


L’equazione è ovviamente a variabili separabili. Qui però non poniamo il denominatore diverso da zero, poiché tale condizione è già contenuta all’interno della risoluzione. Quel passaggio aggiuntivo lo si fa solo quando siamo noi che andiamo a dividere e cambiare ciò che abbiamo. Quindi, risolviamola come sappiamo fare.

\frac{dy}{dx} = \frac{\cos x}{\cos y}

Isoliamo le variabili al loro posto:

\cos y \; dy = \cos x \; dx

Integriamo tutto:

\int \cos y \; dy = \int \cos x \; dx

Risolviamo facilmente gli integrali, vedendo nella tabella degli integrali definiti.

\sin y = \sin x + c

Ogni volta che abbiamo la variabile (in questo caso vogliamo la y) dentro una funzione (il seno), dobbiamo applicare la sua funzione inversa:

y = \arcsin ( \sin x + c )

L’esercizio è concluso!

Esercizio 5. y' = \frac{y^3}{1+x^2}


Passiamo subito al sodo qui. Provate a farlo voi questo, e poi rivenite a vedere la soluzione.

\frac{dy}{dx} = \frac{y^3}{1+x^2}

\frac{dy}{y^3} = \frac{dx}{1+x^2}

Qui abbiamo noi diviso e portato la y al denominatore. Quindi dobbiamo continuare, ma supponendo per il momento che y^3 \ne 0 \implies y \ne 0 ! Integriamo poi:

\int \frac{dy}{y^3} = \int \frac{dx}{1+x^2}

\frac{y^{-2} }{-2} = \arctan x +c

Riscriviamo l’esponenziale della y in una forma comoda:

- \frac{ 1}{2y^2} = \arctan x +c

L’obiettivo è sempre isolare la y!

- \frac{ 1}{2} = y^2 (\arctan x +c )

- \frac{ 1}{2(\arctan x +c ) } = y^2

Ossia:

- \frac{ 1}{2\arctan x +2c } = y^2

Come già detto in precedenza, la costante la possiamo denominare come vogliamo, quindi possiamo anche riscrivere 2c come solo c.

- \frac{ 1}{2\arctan x +c } = y^2

La soluzione sarà le due radici:

y = \pm \sqrt{- \frac{ 1}{2\arctan x +c } }

E questo è il primo risultato. Come sempre, se il libro porta un altro risultato può essere necessario fare qualche altro passaggio, non necessario però.

Dobbiamo adesso fare questo famoso passaggio aggiuntivo, per verificare se y=0 è soluzione. Vediamo se esce che y’=0:

y' = \frac{y^3}{1+x^2}

y' = \frac{0}{1+x^2} = 0

Ed allora deduciamo che anche y=0 è soluzione da prendere!

Domande frequenti sulle equazioni differenziali a variabili separate

Vediamo le domande più frequenti che ci vengono poste su questo argomento.

Perché si scrive una sola c quando si integra?

Quando risolviamo gli integrali, quindi quando abbiamo:

\int ... = \int ...

Perchè poi si mette una sola +c se ci sono due integrali? La risposta è che “c” è una costante arbitraria, che definiamo noi, diversa per ogni integrale. Quindi uscirebbe fuori:

.... + c_1 = ... + c_2

.... = ... + c_2 - c_1

E chiamiamo la differenza di queste due costanti integrative semplicemente c.

Perché y=0 è soluzione se y’ = 0?

Quando abbiamo a che fare col famoso “passaggio aggiuntivo” che abbiamo visto più volte nel corso di questa pagina, abbiamo detto che y=0 risultava soluzione solo se usciva fuori y’=0. Ma perché?

La risposta vi può sorprendere per quanto semplice: se y=0 la sua derivata dovrà essere y’=0 chiaramente! La derivata di una costante (zero in questo caso) deve fare zero. Quindi dobbiamo verificare questa uguaglianza ovvia.

La pagina è conclusa, speriamo che sia stato chiaro il tutto. Se avete dubbi o altre domande da inserire in questa pagina, mandateci la domanda su mondofisica.contatto@gmail.com e la riporteremo su questa pagina!