Equazioni di primo grado: 20 ESERCIZI SVOLTI
Equazioni di primo grado: 20 ESERCIZI SVOLTI! In questa pagina vedremo come risolvere le equazioni, spiegando i passaggi da seguire e facendo insieme 20 esercizi svolti e con soluzione. Sarete pronti per la verifica in classe! Vi basteranno dunque qualche giornata su questa pagina per imparare a svolgere le equazioni. Gli esercizi saranno in ordine di difficoltà.
Indice
- I passaggi da seguire
- Esercizi sulle equazioni FACILI
- Esercizi sulle equazioni MEDI
- Esercizi sulle equazioni DIFFICILI
- Equazioni con parametri
Iniziamo subito e non perdiamoci in chiacchiere!
I passaggi da seguire
Di seguito mostriamo in breve i passaggi generali che si dovranno andare a seguire in ogni esercizio. Fare gli esercizi è importante perché possono capitare diverse cose particolari.
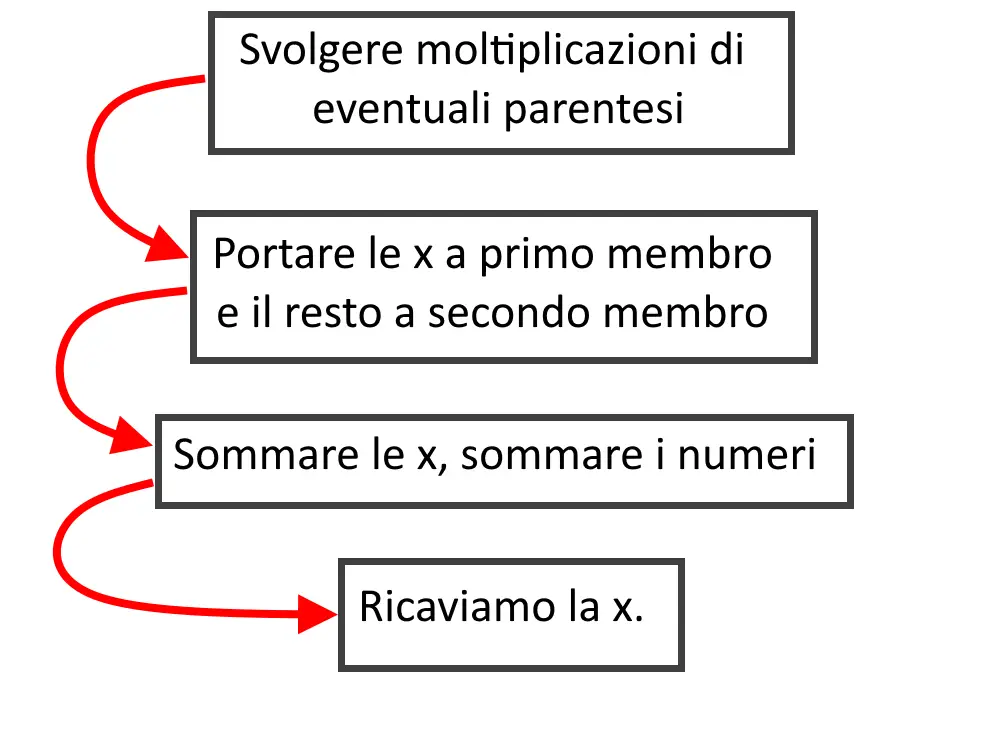
Andiamo agli esercizi svolti sulle equazioni di primo grado!
Esercizi sulle equazioni FACILI
Esercizio 1. 2x- 7 = -3x + 3
Il nostro obiettivo è ricavare la x. Come vedete non abbiamo parentesi, né moltiplicazioni da svolgere, né minimi comuni multipli da fare, né nulla: l’equazione ha sole somme. Possiamo quindi direttamente passare al portare i termini con le x a primo membro (a sinistra):
2x- 7 +3x = + 3
RICORDATE: quando si passa da una parte all’altra un termine, lo si cambia di segno!
Poi, portiamo il -7 a destra. In questo modo abbiamo tutti termini con le x a sinistra, e tutti i numeri a destra.
2x +3x = + 3 +7
Ora possiamo sommare separatamente ciò che sta a sinistra e ciò che sta a destra! Cioè per esempio possiamo ovviamente sommare 3+7 che fa 10.
2x +3x = 10
A sinistra pure possiamo sommare i termini con la x. Come si fa? Si sommano i coefficienti (2+3), e poi si aggiunge davanti una x!
5x = 10
Ora che abbiamo un solo termine a sinistra, ed un solo termine a destra, ricaviamo la x. Per farlo dobbiamo levare quel 5 dalla x: quindi dividiamo tutto per 5.
\frac{5x}{5} = \frac{10}{5}
Semplifichiamo il 5:
x= \frac{10}{5}
La frazione la si può semplificare dividendo numeratore e denominatore per 5, e quindi esce 2:
x= 2
La x è stata trovata, l’esercizio è concluso!
Esercizio 2. 3x- 2 +2x= 6 -2
Osserviamo l’equazione con calma: non ci sono evidenti calcoli da svolgere, passiamo dunque a portare semplicemente il -2 a destra. A sinistra già ci sono tutte le x! Questo passaggio lo potete fare uno alla volta, o tutto insieme. Se siete alle prime armi fate sempre un passaggio alla volta per evitare di sbagliare!
3x +2x= 6 -2 +2
Sommiamo, come fatto nell’esercizio precedente:
5x= 6
Adesso che abbiamo un numero a destra ed un termine da solo a sinistra, possiamo andare a ricavare la x. Dobbiamo sbarazzarci del 5 davanti alla x: dividiamo tutto per 5.
\frac{5x}{5}= \frac{6}{5}
Semplifichiamo il 5 a primo membro, mentre a destra non si può fare nulla, quindi lasciamo la frazione così com’è!
x = \frac{6}{5}
Finito!
Esercizio 3. x- 9 = 2x + 6
Questo è un bell’esercizio, vediamo dopo perché! Portiamo le x a primo membro, ed il resto lo teniamo al secondo.
x-2x = 6 +9
Sommiamo i rispettivi termini, e notiamo che la x appare negativa! (perché 1-2=-1)
-x = 15
La soluzione così non va bene, noi vogliamo che ci sia solamente la x, senza nient’altro. Moltiplichiamo allora tutto per -1!
-1 \cdotp (-x) = -1 \cdotp 15
Essendo che – per – fa +, segue che:
x = -15
Come vedete, questo è equivalente a “cambiare tutto di segno”. Esso è molto utilizzato nelle equazioni, quindi prendete nota!
Esercizio 4. 15x- 9 = 30(x -1)
Osserviamo l’esercizio che ci dà il libro: c’è una parentesi, dobbiamo quindi levarci da mezzo prima quella. Effettuiamo la moltiplicazione del 30 per (x-1) innanzitutto:
15x- 9 = 30x -30
RICORDATE: il 30 moltiplica tutti i termini che stanno dentro la parentesi, non solo il primo!
Ora siamo pronti per portare tutto da un lato e dall’altro, facciamolo!
15x- 30x = +9 -30
E sommiamo:
-15x = -21
Ora, come fatto nell’esercizio precedente moltiplichiamo tutto per -1, o in breve “cambiamo tutto di segno”.
15x = 21
Adesso dividiamo tutto per 15 per isolare la x e concludere l’esercizio trovando la x.
x = \frac{21}{15}
Si può semplificare la frazione essendo che i due termini sono dividibili per 3:
x = \frac{7}{5}
Se siete durante un compito in classe e non sapete se vi trovate o no, potete effettuare una verifica della soluzione.
Esercizio 5. 2(x+ 7) +4 = 4+ 3 (1-x)
Guardiamo prima di tutto l’esercizio in faccia, cosa che vi consiglio sempre per qualsiasi esercizio per capire cosa fare prima. Abbiamo due parentesi da svolgere, facciamolo:
2x+ 14 +4 = 4+ 3 -3x
Uno alla volta (attenti che sono tanti termini) portiamo a primo membro e al secondo i vari numeri e x:
2x+3x = 4+ 3 -14 -4
Adesso sommiamo, controlliamo sempre più volte ogni passaggio per evitare di sbagliare un banale segno.
5x = -21
E dividendo per 5, otteniamo la soluzione dell’equazione di primo grado!
x = - \frac{21}{5}
Esercizio 6. - \frac{7}{2} x = 0
E questa come la si risolve? Alla fine dell’esercizio vi diremo un modo velocissimo per capire la soluzione di equazioni di primo grado di questo tipo. Però per ora vi facciamo vedere il procedimento passo dopo passo. Allora: non ci sono parentesi, la x sta a sinistra e lo 0 (numero) sta a destra, quindi possiamo passare ad isolare la x. Partiamo dal cambiare tutto di segno:
\frac{7}{2} x = 0
(dove abbiamo usato che -0 = 0)
Ora moltiplichiamo tutto per 2, per levare il denominatore:
2\frac{7}{2} x = 2 \cdotp 0
La frazione si semplifica, mentre un qualsiasi numero moltiplicato per zero dà sempre zero, quindi:
7 x = 0
Ci è rimasto solo il 7 attaccato alla x, dividiamo tutto per 7:
\frac{7 x}{7} = \frac{0}{7}
La frazione se ne va, e rimane solo la x. Poi altra cosa: zero diviso per qualsiasi numero (diverso da zero) dà ancora zero. Di conseguenza la soluzione è:
x= 0
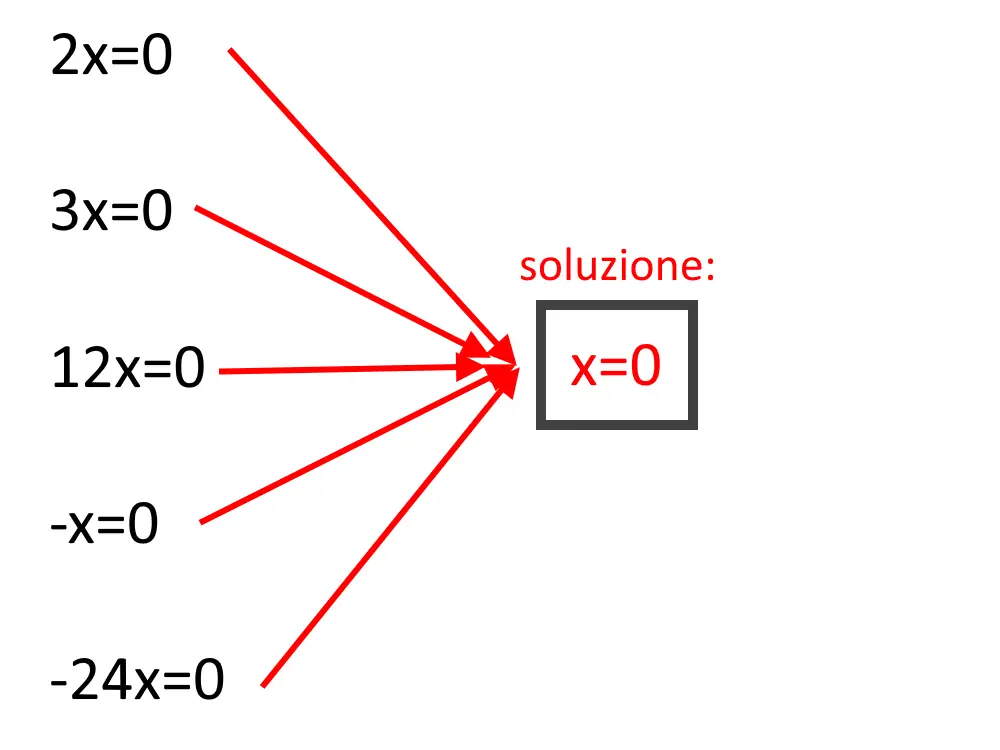
A questo potevamo arrivarci fin dall’inizio, perché ogni volta che avete un qualcosa di questo tipo, la soluzione è sempre x=0! Tenetelo a mente!
Esercizio 7. -2(3y-1) +4y = 3(1-5y)
Qui abbiamo una y e non una x, come fare? Chiamare una variabile x o chiamarla y o z, o anche “giuseppe” è uguale, non cambia nulla! Semplicemente assume un nome diverso. Infatti questa è sempre una equazione di primo grado, ma con una variabile y, tutto qui.
Come sempre allora svolgiamo le parentesi:
-6y + 2 +4y = 3-15y
-6y +4y +15y = 3-2
Sommiamo i termini corrispondenti come sempre:
13y = 1
E ricaviamo la soluzione dividendo tutto per 13.
y = \frac{1}{13}
Ecco fatto, ora si chiama y, e prima si chiamava x, è solo un nome!
Continuiamo con altre equazioni esercizi svolti! Passiamo adesso ad un gradino leggermente superiore, equazioni di primo grado di livello medio!
Esercizi sulle equazioni livello MEDIO
Esercizio 8. \frac{2}{3}(x+2) = \frac{4}{30}(2x+1)
Qui abbiamo due parentesi da svolgere, dove dobbiamo moltiplicarle per delle frazioni come vedete. La moltiplicazione per una frazione è particolare, può portare ad errori evitabilissimi, quindi facciamo davvero un passaggio alla volta con calma:
\frac{2}{3}x+ \frac{2}{3} \cdotp 2 = \frac{4}{30} \cdotp 2x+ \frac{4}{30}
RICORDATE: potete semplificare solo fra numeratore e denominatore.
Otteniamo quindi:
\frac{2}{3}x+ \frac{4}{3} = \frac{4}{15} x+ \frac{4}{30}
E’ cosa utile rimanere la x scritta in questa maniera, ossia scritta di fianco alla frazione.
Adesso portiamo da un lato e dall’altro i rispettivi termini:
\frac{2}{3}x -\frac{4}{15} x= + \frac{4}{30} - \frac{4}{3}
Adesso facciamo due minimi comuni multipli separati, uno per le x ed uno per i numeri:
\frac{10x-4x}{15}x = \frac{4-40}{30}
Effettuiamo la somma ai numeratori:
\frac{-6x}{15} = \frac{-36}{30}
Adesso abbiamo un bel po’ di roba da levare di mezzo. Iniziamo a far scomparire i denominatori: moltiplichiamo tutto per 30:
30 \frac{-6x}{15} = 30 \frac{-36}{30}
-12x = -36
Cambiamo tutto di segno:
12x = 36
E poi dividiamo per 12!
x = 3
Esercizio 9. 3(1+2x) = -5[-x+2(-x-3) ]
Qui per la prima volta incontriamo le parentesi quadre. Una regola fondamentale da ricordare è che si calcolano prima le parentesi tonde, poi le quadre ed infine quelle graffe. Quindi teniamo da parte un attimo quella quadra, e concentriamoci sul levare quelle tonde:
3+6x = -5[-x-2x-6 ]
Ora che le parentesi tonde sono state eliminate, possiamo passare a quelle quadre, e fare lo stesso:
3+6x = +5x+10x+30
Da qui sappiamo come concludere l’esercizio! Provate stesso voi prima e poi controllate!
6x -5x-10x= 30-3
-9x= 27
Cambiamo di segno e dividiamo per 9, la soluzione dell’equazione di primo grado lineare è:
x= - 3
Esercizio 10. 3x(x-2) = x -2 +3x^2
Questa risulterà comunque un esercizio sulle equazioni di primo grado! Anche se figurano termini quadratici come 3x^2 alla fine dei conti se ne andranno via, e ritornerà una equazione di primo grado normale. Quindi nel compito per vedere se state facendo bene controllate che se ne vadano via!
Comunque il procedimento non cambia in generale, svolgiamo sempre le moltiplicazioni e sciogliamo la parentesi:
3x \cdotp x -2 \cdotp 3x = x -2 +3x^2
3x^2 - 6x = x -2 +3x^2
Portiamo le x a primo membro (anche quelle quadratiche del tipo x^2):
3x^2 - 6x - x - 3x^2= -2
E come prova del fatto che stiamo andando bene i termini sommati se ne vanno via! (3-3)
-7x = -2
Cambiamo tutto di segno e poi dividiamo per 7, la soluzione di questa equazione di primo grado è:
x = \frac{2}{7}
Esercizio 11. 6x (4-x) = -2x(3x-1) + 14x
Sciogliamo le parentesi, e poi noteremo che anche qui usciranno termini quadratici.
24x -6x^2 = -6x^2 +2x + 14x
Portiamo tutti i termini a primo membro in pratica, visto che di numeri puri non ce ne sono.
24x -6x^2 +6x^2 -2x - 14x = 0
Come conferma notiamo che i termini quadratici se ne vanno via, quindi ritorna una equazione di primo grado che sappiamo risolvere.
8x = 0
Questa l’abbiamo già vista nell’esercizio 6. Quando abbiamo un qualcosa di questo tipo, la soluzione è sempre:
x=0
Esercizio 12. 7(2+3x) -10x = 3(2x-1) + 5(x+1) + 12
Questo è un esercizio molto importante, dopo vedremo perché. Iniziamo dal togliere queste parentesi tonde che vi compaiono:
14+21x -10x = 6x-3 + 5x+5 + 12
21x -10x -6x -5x= -14 -3 +5 + 12
Sommando notiamo che viene la seguente strana cosa:
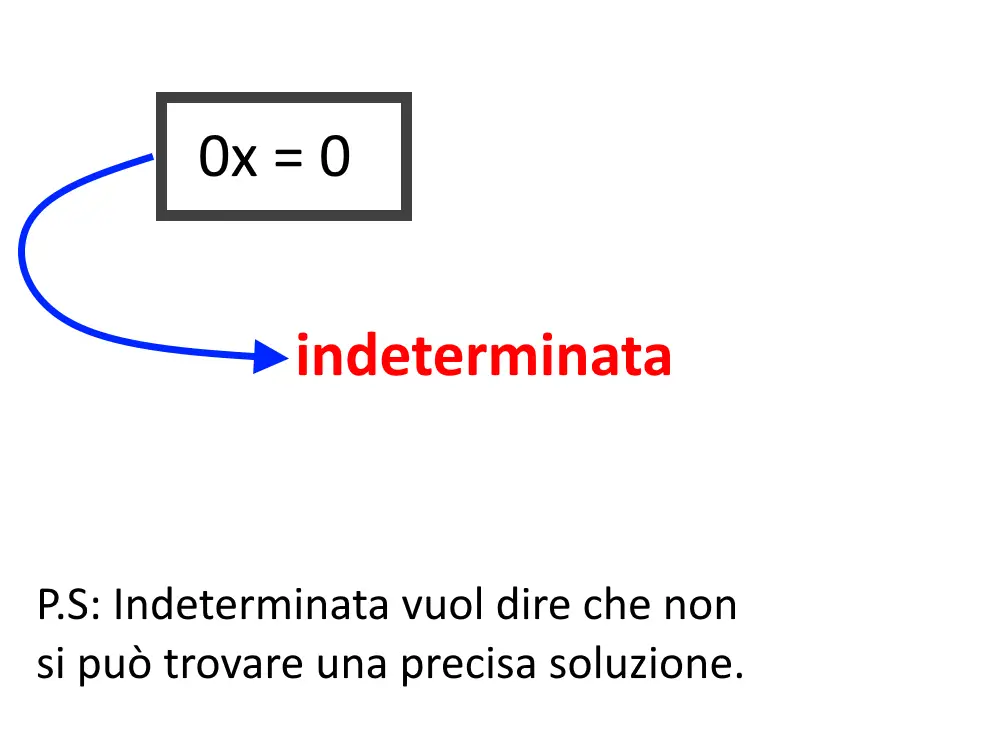
0x= 0
Questa tipica forma di equazione si dice che non si può trovare una soluzione precisa, quindi essa è indeterminata.
Questo avviene perché se ricavate la x, si ottiene:
x= \frac{0}{0}
E zero fratto zero non esiste!
Esercizio 13. [27 + (-3)^3]x = 9
Anche qui come qualche esercizio fa compaiono più parentesi: la regola dice che si parte sempre da quella tonda. Se non vi ricordate come funzione una potenza, essa è un numero moltiplicato per sè stesso tot volte, quindi:
(-3)^3 = -3 \cdotp -3 \cdotp -3 = -27
Di conseguenza:
[27 -27 ]x = 9
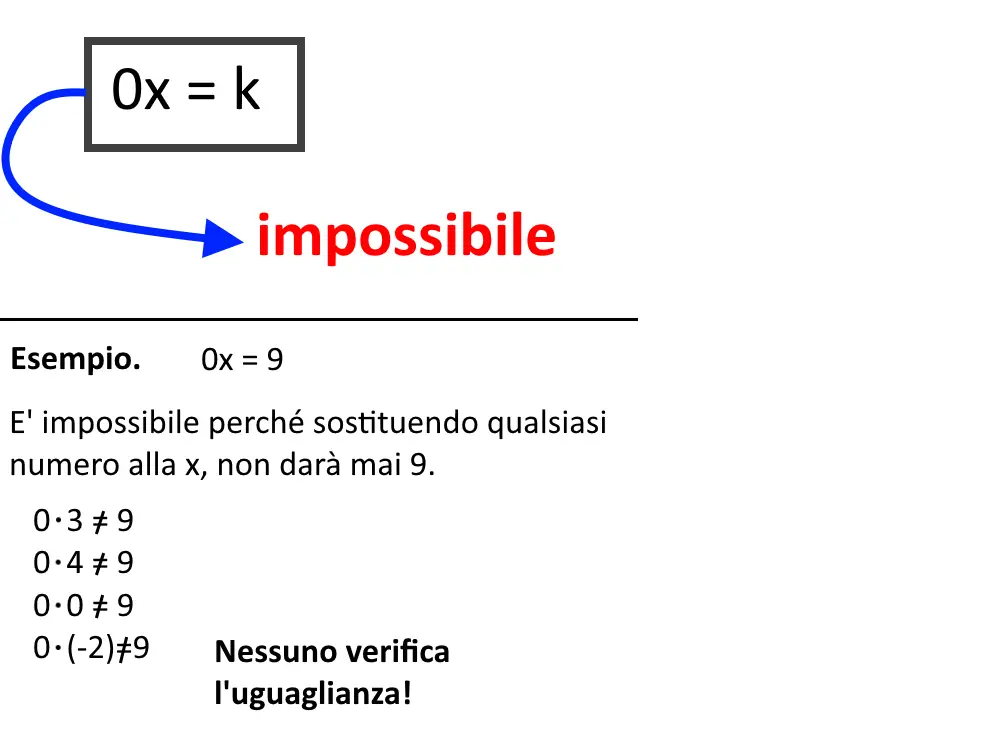
0x = 9
Qui otteniamo l’ultima forma di equazione di primo grado strana che vi può capitare. Essa non ha soluzione, ed è impossibile.
Perché non ha soluzione? Provate a sostituire qualsiasi numero alla x per effettuare una verifica: notiamo che non c’è nessun numero che moltiplicato per 0 dia 9, perché ovviamente qualsiasi numero moltiplicato per 0 darà sempre zero e mai 9!
Esercizio 14. (3x-2)(9x^2 +6x +4) = 9x(3x^2 -2) -8
Qui compare una moltiplicazione fra due parentesi. Se non vi ricordate come si fanno, vi basta sapere che dovete moltiplicare i termini delle due parentesi, in tutte le loro combinazioni. Vi verrà dunque:
27x^3 + 18x^2 +12x -18x^2 - 12x - 8= 27x^3 -18x -8
Qui vengono fuori anche termini cubici, che per far sì che vi si ritorni ad una equazione di primo grado, c’è bisogno che vadano via.
27x^3 + 18x^2 +12x -18x^2 - 12x -27x^3 +18x = -8+8
18x = 0
Tale forma, come visto, ha come soluzione sempre x=0!
Aumentiamo ancora di più il livello, passando ad esercizi equazioni difficili!
Esercizi sulle equazioni con soluzione DIFFICILI
Esercizio 15. 4 (x - \frac{1}{2} )^2 -3x +1 = (2x+3)^2 -19x +2
Qui compaiono due quadrati di un binomio. Seguiremo quindi la seguente formula.
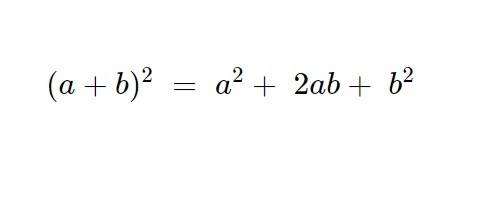
Di conseguenza, nel nostro esercizio avremo che:
4 (x^2 + \frac{1}{4} -x ) -3x +1 = (4x^2+9 + 12x) -19x +2
Sciogliamo le parentesi:
4x^2 + 4\frac{1}{4} -4x -3x +1 = 4x^2+9 + 12x -19x +2
4x^2 + 1 -4x -3x +1 = 4x^2+9 + 12x -19x +2
E seguiamo la solita procedura.
4x^2 -4x -3x - 12x +19x -4x^2 = +9 +2-1-1
0x = 9
Questa forma, che spero abbiate segnato su un foglietto, ha come soluzione:
impossibile
Esercizio 16. (x-2)^2 - (x-3)(x+3) = 2x + 4
Se osserviamo l’equazione notiamo un quadrato di un binomio e poi anche un’altra cosa. Il termine (x-3)(x+3) ci fa ricordare la formula della differenza di quadrati.
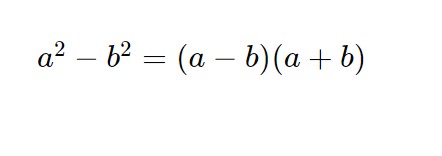
Adottando tali formule in questo esercizio, ricaviamo che:
x^2 + 4 -4x - (x^2 - 9 ) = 2x + 4
Come potete vedere, a volte le parentesi è meglio tenerle, per evitare di sbagliarci, visto che ora dobbiamo poi moltiplicare quella parentesi per un segno meno!
x^2 + 4 -4x - x^2 + 9 = 2x + 4
x^2 -4x - x^2 -2x = + 4 -4 -9
Sommiamo i termini simili dunque:
-6x = -9
Con soluzione dell’esercizio:
\implies x = \frac{3}{2}
Esercizio 17. (a-2)^3 + (a-5)(a+5) - a (1+a^2) = -5a^2 + 4a -2
Qui figura oltre ad un evidente differenza di quadrati, anche un cubo di un binomio.
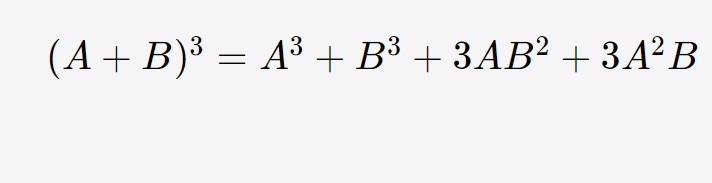
Con i nostri dati otteniamo:
a^3 -8 -6a^2 + 12a + a^2-25 - a - a^3 = -5a^2 + 4a -2
a^3 -6a^2 + 12a + a^2 - a - a^3 +5a^2 - 4a = -2+25+8
I termini cubici, come prova che stiamo andando bene, se ne vanno, e si elidono anche quelli quadratici! Quello che rimane è:
7a = 31
\implies a = \frac{31}{7}
Esercizio 18. (a - a^2 -1)^2 - 3 (a+2)^2 = a^3 (a-1) +a [(a+2)(1-a) +a ]
Qua c’è un miscuglio di un po’ di tutto! Quando sono così lunghi andate con calma. In più vediamo anche un’altra formula utile: quella del quadrato di un trinomio.
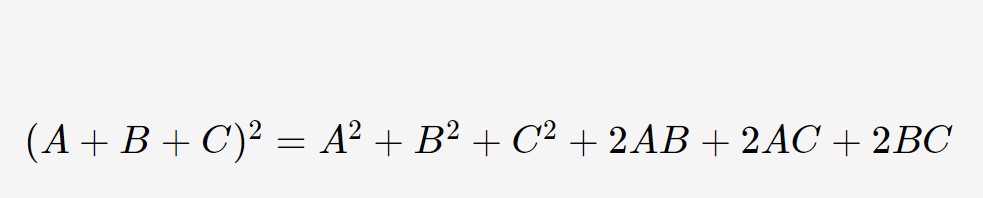
Applicando le varie formule che servono, otteniamo la lunga equazione seguente:
a^2 + a^4 +1 -2a^3 -2a +2a^2 - 3 (a^2+4 + 4a) = a^4 -a^3 +a [ a - a^2 +2 -2a +a ]
Vista la grandissima lunghezza, una cosa che può dare sicurezza è che fra un paio di passaggi tutti i termini quadratici, cubici e alla quarta se ne vanno. Vediamo! Intanto, leviamo anche le rimanenti parentesi:
a^2 + a^4 +1 -2a^3 -2a +2a^2 - 3a^2-12 -12a = a^4 -a^3 a^2 - a^3 +2a -2a^2 +a^2
a^2 + a^4 -2a^3 -2a +2a^2 a^2-12 -12a - a^4 +a^3 - a^2 + a^3 -2a +2a^2 -a^2= -1 +12
E di conseguenza ci troviamo, perché se ne vanno tutti via e ritorna ad essere una equazione di primo grado:
-2a -12a -2a = -1 +12
-16a = 11 \implies a = - \frac{11}{16}
Ed abbiamo concluso finalmente!
Passiamo adesso ad un paio di esercizi svolti di equazioni di primo grado contenenti parametri.
Esercizi equazioni con parametri
Esercizio 19. Trova per quale valore di a la seguente equazione risulta essere indeterminata.
5 (a+2)x = 4a + 8
Risolvere una equazione con parametri significa risolvere una equazione in cui a è un parametro: ossia all’inizio non ha un valore preciso, ma è variabile. L’esercizio ci dà però un grande utile dato: l’equazione deve risultare indeterminata.
Indeterminata significa che essa dovrà essere della forma seguente:
0x = 0
Cioè dobbiamo scegliere un valore di a tale che sia il membro di sinistra che quello di destra risulti 0. Questo è equivalente a dire che dobbiamo risolvere il seguente sistema:
\begin{cases} 5 (a+2) = 0 \\ 4a + 8 = 0 \end{cases}
Questo sistema ci dovrà dare uno stesso valore di a, altrimenti diremo che è non è possibile che sia determinata.
\begin{cases} 5a+10 = 0 \\ 4a + 8 = 0 \end{cases}
\begin{cases} a = -2 \\ a = -2 \end{cases}
Il sistema accorda per una comune soluzione a=-2, e quindi grazie a tale valore l’equazione sarà indeterminata!
Esercizio 20. Trova per quale valore di a la seguente equazione ammette come soluzione x=0.
4(x+a) = a(3-x) - 2(2x-a) + 6
L’esercizio ci dice che tale equazione deve avere come soluzione x=0, quindi è una specie di verifica della soluzione. Quindi basterà sostituire lo 0 alla x, e trovare il valore di a, risolvendo l’equazione in variabile a che ne esce fuori.
4(0+a) = a(3-0) - 2(0-a) + 6
4a = 3a +2a + 6
Portiamo i termini con la a primo membro, come se fosse una normale equazione!
4a -3a -2a = 6
-a = 6 \implies a = -6
Abbiamo visto in questa pagina come risolvere esercizi equazioni di primo grado!
Trovate altre centinaia di esercizi svolti di argomenti vari di matematica, geometria e geometria analitica!
Per approfondire:
https://it.wikipedia.org/wiki/Equazione
verifica
equazioni