Equazioni goniometriche: ESERCIZI SVOLTI
Equazioni goniometriche: ESERCIZI SVOLTI! In questa pagine vedremo tutti i tipi di esercizi svolti di equazioni goniometriche. Se non avete mai approcciato con le equazioni goniometriche, vi consigliamo prima di vedere e capire come svolgere esercizi sulle equazioni goniometriche elementari. Detto questo iniziamo subito!
Indice
- Equazioni goniometriche riconducibili a quelle elementari
- Equazioni lineari in seno e coseno
- Equazioni di 2° grado in seno e coseno
Prima di iniziare questo nuovo capitolo, ricordatevi di ripetere prima le equazioni goniometriche elementari! Vediamo subito degli esercizi svolti equazioni goniometriche riconducibili a quelle elementari!
Equazioni goniometriche
riconducibili a quelle ELEMENTARI
Esercizio 1. 2 \cos^2 x - \cos x = 0
Questo tipo di esercizi di equazioni goniometriche sono riconducibili alle equazioni goniometriche elementari, ossia utilizzando qualche piccolo trucchetto, come mettere in evidenza o utilizzare le formule goniometriche, ritroviamo equazioni elementari che sappiamo già risolvere.
In questo caso ad esempio notiamo che mettendo in evidenza il coseno otteniamo:
\cos x (2 \cos x -1) = 0
Questo è un prodotto che si deve annullare, quindi questo ha come soluzioni:
\cos x = 0
Oppure:
2 \cos x -1 = 0
Come vedete sono entrambe equazioni goniometriche elementari, risolviamole una per volta: partiamo dalla prima.
\cos x = 0
Questa si risolve disegnando una circonferenza goniometrica, e la retta X=0, essendo un coseno. Vediamo poi dove si intersecano, e quelle sono le nostre soluzioni.
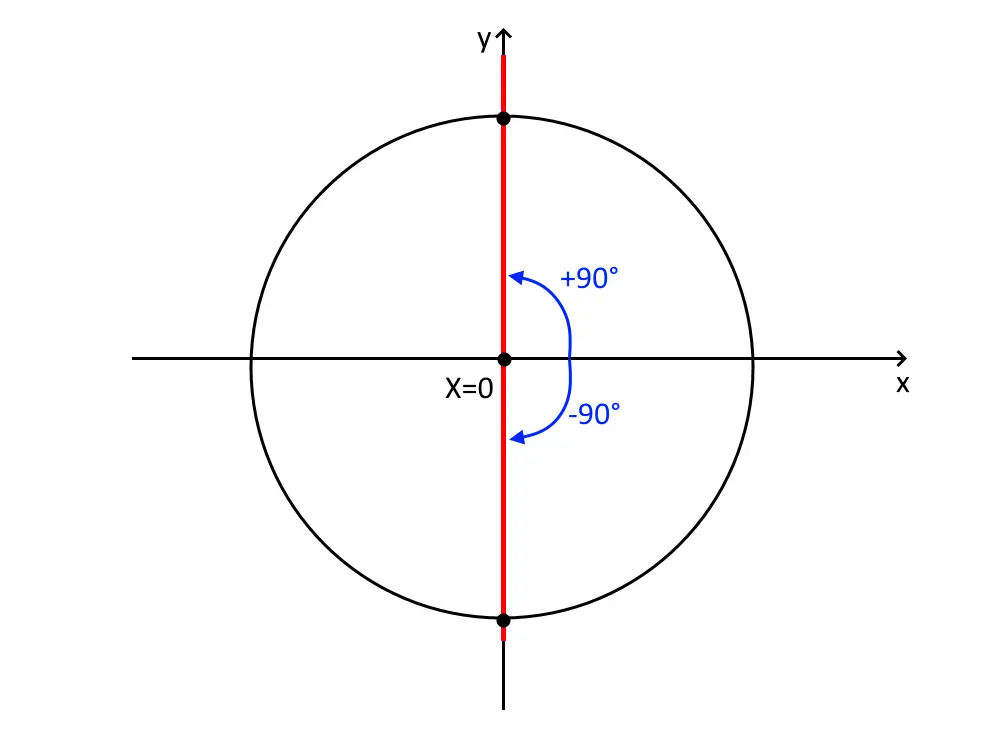
Quindi le soluzioni di questa prima equazione goniometrica elementare è:
x= \pm \frac{\pi}{2} + 2k \pi
Passiamo all’altra equazione goniometrica elementare:
2 \cos x -1 = 0
Isoliamo il coseno:
\cos x = \frac{1}{2}
Disegniamo la retta X=\frac{1}{2} , dove la soluzione è data dalla calcolatrice che ci dice il primo angolo.
Cioè sulla calcolatrice premete in alto a sinistra shift poi premete il coseno (in questo caso), aprite la parantesi tonda e scrivete 1:2, poi chiudete la parentesi tonda ed il gioco è fatto. Vi darà 60° che in radianti è \frac{\pi}{3} e poi ci aggiungete 2k\pi che è la periodicità del coseno.
L’altro come si nota dal disegno è lo stesso ma con segno opposto, per cui:
x= \pm \frac{\pi}{3} + 2k \pi
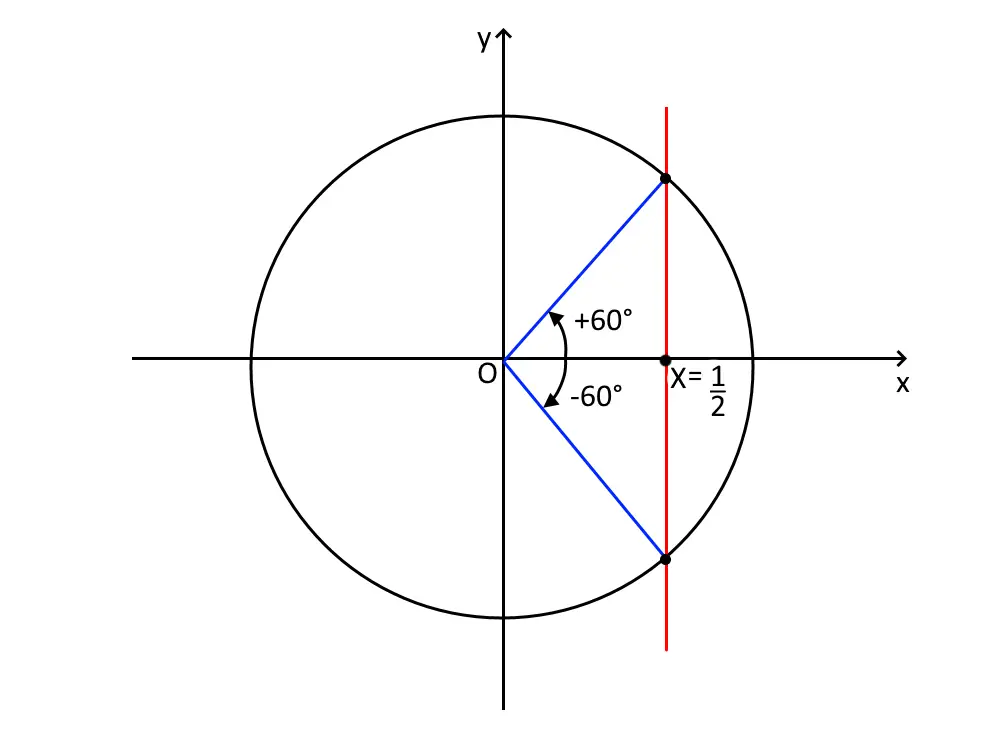
Per cui le soluzioni sono:
x= \pm \frac{\pi}{2} + 2k \pi \\ \lor x= \pm \frac{\pi}{3} + 2k \pi
Esercizio 2. 2 \sin^2 x - 1 = 0
Iniziamo ad isolare il seno, che è la prima cosa che ci viene in mente:
\sin^2 x = \frac{1}{2}
La presenza di quel quadrato ci dà fastidio perché non possiamo levarlo. Qui possiamo dirvi un primo prezioso consiglio: quando c’è un seno o un coseno o una tangente al quadrato, si procede per sostituzione. Questo in genere quando avete dei quadrati si procede nel modo seguente. Cioè si pone:
\sin x = t
E di conseguenza l’equazione goniometrica diventa:
t^2 = \frac{1}{2}
Cioè un equazione con termine quadratico che sappiamo risolvere. La sua soluzione è le due radici con segni opposti:
t = \pm \frac{1}{ \sqrt{2} }
Razionalizziamo:
t = \pm \frac{1}{ \sqrt{2} } \frac{ \sqrt{2} }{ \sqrt{2} } = \pm \frac{ \sqrt{2} }{2}
Risostituiamo e quindi torniamo alla x:
\sin x = \pm \frac{ \sqrt{2} }{2}
Quindi siamo arrivati a due equazioni goniometriche elementari, che sappiamo risolvere. Partiamo dalla prima, quella col segno +:
\sin x = + \frac{ \sqrt{2} }{2}
Disegniamo una circonferenza goniometrica, e tracciamo la retta Y=\frac{ \sqrt{2} }{2} trattandosi di un seno.
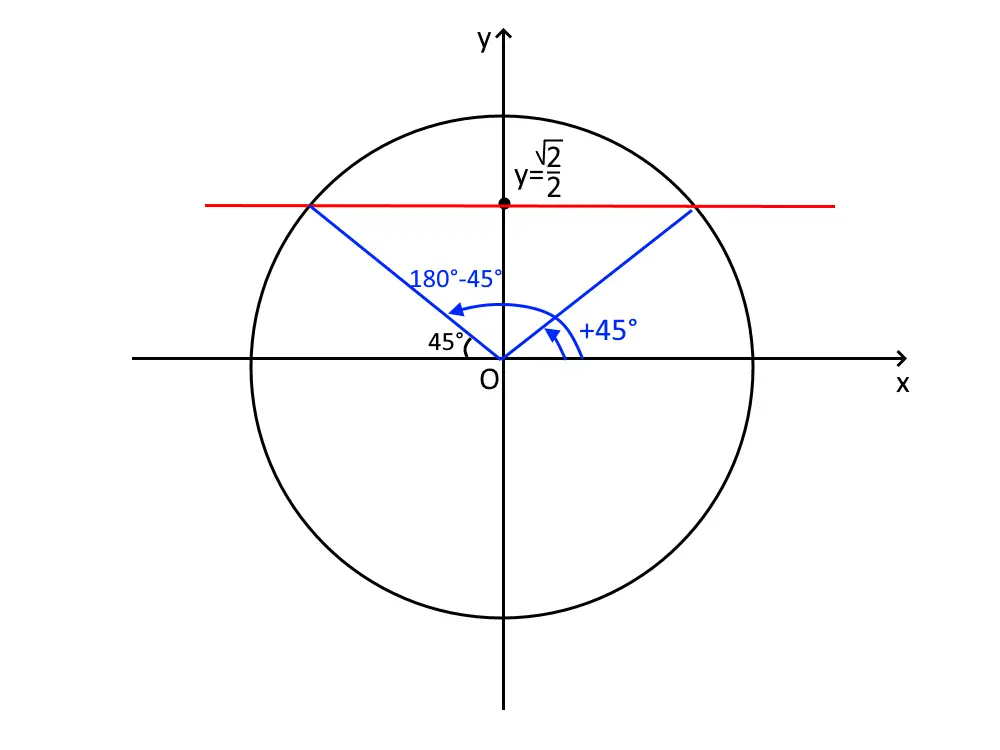
La prima soluzione ce la dà la calcolatrice e ci dice:
x=\frac{\pi}{4} + 2k \pi
L’altra ci si arriva guardando il disegno, notiamo infatti che l’altro angolo è:
x= \pi - \frac{\pi}{4} + 2k \pi
Facendo il mcm fra i primi due termini:
x= \frac{3}{4}\pi + 2k \pi
Ed abbiamo queste prime due soluzioni. Passiamo allora all’altra equazione goniometrica elementare:
\sin x = - \frac{ \sqrt{2} }{2}
Facciamo il procedimento analogo a prima, quindi tracciamo la retta Y=-\frac{ \sqrt{2} }{2} in una circonferenza goniometrica. La prima soluzione che ci dà la calcolatrice è:
x= - \frac{\pi}{4} + 2k \pi
E l’altra notiamo che è:
x= \pi + \frac{\pi}{4} + 2k \pi
x= \frac{5}{4}\pi + 2k \pi
Il libro vi potrebbe dare una soluzione compattata, quel procedimento di compattare le soluzioni non è necessario, è uguale e va bene lo stesso!
Esercizio 3. 2 \cos^2 x - \sin x - 1 = 0
Qui notiamo un coseno al quadrato, ma non possiamo subito procedere per sostituzione, perché abbiamo anche un seno. Quindi la cosa migliore da fare è rendere il tutto in termini di seno, utilizzando la prima relazione fondamentale della goniometria, ossia:
\sin^2 x + \cos^2 x = 1
\implies \cos^2 x = 1 - \sin^2 x
Quindi l’equazione goniometrica diventa:
2 (1 - \sin^2 x) - \sin x - 1 = 0
2 - 2 \sin^2 x - \sin x - 1 = 0
Sommiamo i rispettivi termini:
- 2 \sin^2 x - \sin x + 1 = 0
Adesso abbiamo tutto in seno, ed un quadrato: ora sì che possiamo procedere per sostituzione, come prima. Poniamo:
\sin x = t
L’equazione diventa:
- 2 t^2 - t + 1 = 0
Abbiamo una equazione di secondo grado, cambiamo perciò tutto di segno, perché vogliamo il coefficiente a positivo.
2 t^2 + t - 1 = 0
Calcoliamo il delta:
\Delta = b^2 - 4ac = 1+8=9
Delta>0 e quindi esistono due soluzioni, calcoliamole usando la formula:
t_{1,2}= \frac{-b \pm \sqrt{ \Delta } }{2a} = \frac{-1 \pm 3 }{4}
Abbiamo quindi:
t=-1, \; t=\frac{1}{2}
Ritorniamo alla x, risostituendo:
\sin x = -1
Ed il seno è uguale a -1 solamente in:
x=\frac{3}{2} \pi + 2k \pi
E poi l’altra equazione elementare da risolvere:
\sin x = \frac{1}{2}
Disegniamo una circonferenza goniometrica, tracciando la retta Y=\frac{1}{2} .
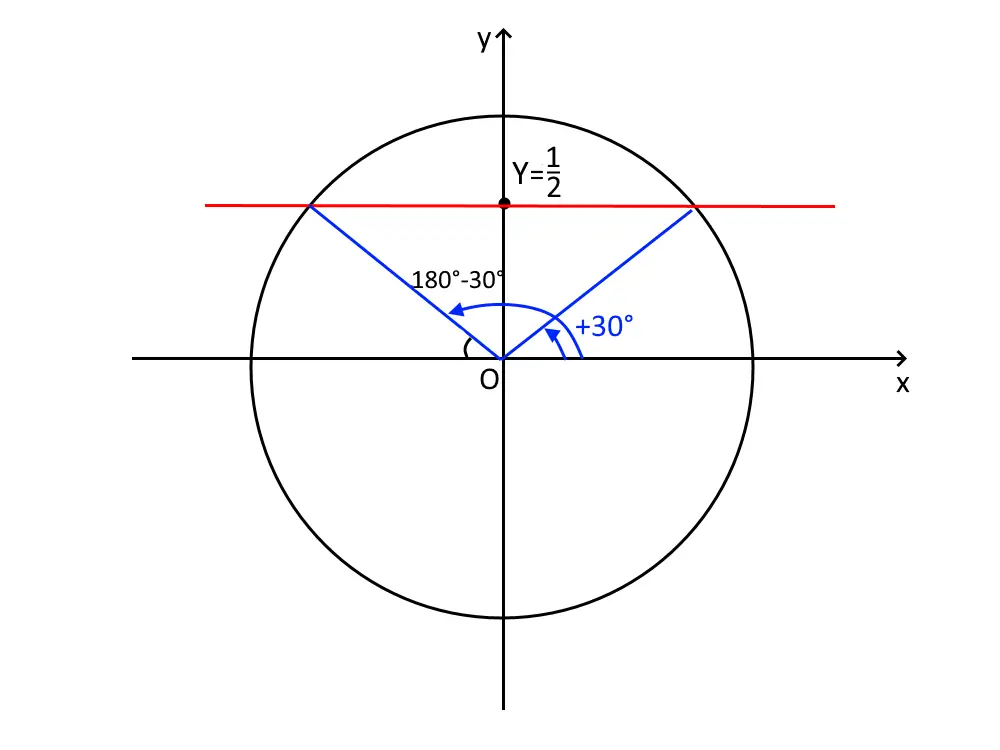
I due angoli soluzione sono:
x= \frac{\pi}{6} + 2k\pi
E l’altro per deduzione:
x= \pi - \frac{\pi}{6} + 2k\pi
x= \frac{5}{6}\pi + 2k\pi
Esercizio 4. 2 \tg x +\cotg x -3 = 0
Ricordando la definizione di cotangente, è possibile riscrivere tutto in termini della sola tangente (più comodo)!
\cotg x = \frac{1}{ \tg x }
Quindi l’equazione goniometrica diventa:
2 \tg x + \frac{1}{ \tg x } -3 = 0
Abbiamo una frazione, quindi prima di andare avanti c’è bisogno di scrivere le condizioni di esistenza (per frazione le CE è denominatore diverso da zero).
CE: \tg x \ne 0 \implies x \ne k\pi
(Il diverso si risolve come l’uguale)
A questo punto possiamo moltiplicare tutto per tg così eliminiamo la forma della frazione:
2 \tg^2 x + 1 -3 \tg x = 0
Come negli esercizi precedenti, abbiamo dei termini della stessa funzione (tangente) ed uno al quadrato: quindi procediamo per sostituzione. Poniamo:
\tg x = t
2 t^2 + 1 -3 t = 0
Quindi è uscita fuori una equazione di secondo grado, riordiniamola:
2 t^2 -3 t +1 = 0
Calcoliamo il delta e poi le soluzioni:
\Delta = b^2 - 4ac = 9-8=1
t_{1,2}= \frac{-b \pm \sqrt{ \Delta } }{2a} = \frac{3 \pm 1 }{4}
E quindi le due soluzioni sono:
t=1, \; t = \frac{1}{2}
Ritorniamo alla x, e risolviamo le due equazioni goniometriche elementari una per volta.
\tg x = 1
Disegniamo una circonferenza goniometrica e poi la retta tangente, con un segmento lungo 1, come segue.
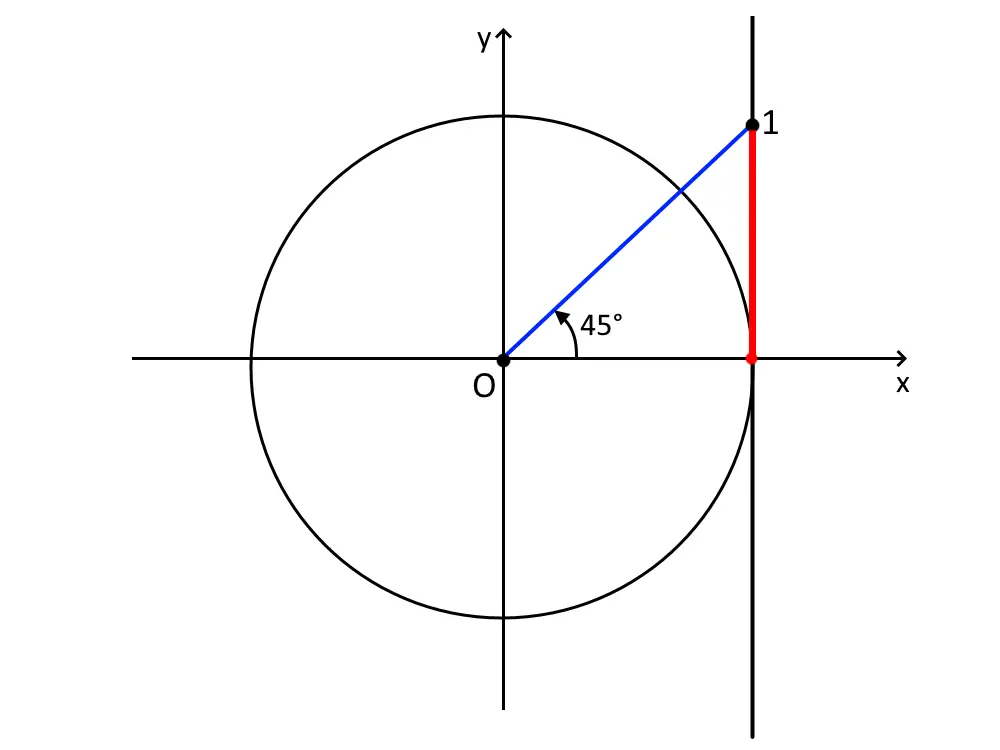
L’angolo soluzione ce lo da la calcolatrice, che è:
x= \frac{\pi}{4} + k \pi
Dove non dimenticatevi che la periodicità della tangente è k \pi .
L’altra invece è:
\tg x = \frac{1}{2}
La soluzione che ci dà la calcolatrice è un angolo complicato, impossibile da scrivere in radianti: quindi lo rimaniamo così con una arcotangente, come segue:
x= \arctg (\frac{1}{2}) + k \pi
Esercizio 5. \sin ( x + \frac{\pi}{6} ) - \frac{1}{2} \cos x = 0
In questa equazione goniometrica appare fin dalla prima vista la presenza della seguente formula di addizione e sottrazione del seno:
\sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta
Utilizziamola ed otteniamo quindi:
\sin x \cos \frac{\pi}{6} + \cos x \sin \frac{\pi}{6} - \frac{1}{2} \cos x = 0
Vediamo alla calcolatrice quanto valgono il seno ed il coseno di quegli angoli. Vi insegno un trucchetto: per sapere che gradi sono per esempio di \frac{\pi}{6} basta fare \frac{180°}{6} = 30° .
\frac{ \sqrt{3} }{2} \sin x + \frac{1}{2} \cos x - \frac{1}{2} \cos x = 0
\frac{ \sqrt{3} }{2} \sin x = 0
Moltiplicando per 2 e dividendo per radical 3:
\sin x = 0
Ed il seno è uguale a zero negli angoli:
x= \frac{\pi}{2} + k\pi
Dove abbiamo direttamente compattato la soluzione. Se non volete farlo allora scriviamo le due soluzioni separatamente (è la stessa identica cosa non vi preoccupate!):
x= \frac{\pi}{2} + 2k\pi
x= \frac{3}{2}\pi + 2k\pi
Abbiamo concluso la sezione degli esercizi svolti equazioni goniometriche riconducibili a quelle elementari. Iniziamo adesso quella relativa alle equazioni goniometriche lineari in seno e coseno!
Equazioni goniometriche LINEARI in seno e coseno
Esercizio 6. \sin x + \cos x = 0
Questo è il caso in cui avete un seno ed un coseno da soli, senza nient’altro. Ossia il caso omogeneo:
a \sin x + b \cos x = 0
Queste si risolvono sempre con lo stesso metodo: si divide tutto per il coseno. Inoltre vista la forma dell’equazione, non serve neanche scrivere le CE (condizioni di esistenza) perché la soluzione che scarteremmo sicuramente non potrà essere soluzione nel caso omogeneo.
Quindi, senza pensieri, dividiamo direttamente per il coseno:
\frac{\sin x}{\cos x} + \frac{\cos x}{\cos x} = 0
Ricordando la definizione di tangente, abbiamo ora una equazione goniometrica elementare in funzione della tangente:
\tg x + 1 = 0
\tg x = -1
E questo, vedendo direttamente sulla calcolatrice, troviamo come angolo soluzione:
x= - \frac{\pi}{4} + k\pi
Quindi, non facciamo altre equazioni goniometriche omogenee perché sono davvero tutte uguali: sempre dividere per il coseno e risolvere l’equazione elementare in tangente!
Esercizio 7. \sqrt{3} \sin x +3 \cos x +3 = 0
Questa è una equazione goniometrica lineare non omogenea invece: queste si risolvono con il metodo grafico, o con le formule parametriche. Cioè ci ritroviamo nel caso:
a \sin x + b \cos x + c= 0
A volte può essere più semplice usare il metodo grafico, altre quello delle formule parametriche. Il metodo grafico lo si può usare sempre, quello con le formule parametriche no. In questo esercizio vi faremo vedere come usare il metodo grafico!
Metodo grafico.
PRIMO PUNTO: passiamo ad effettuare le seguenti sostituzioni (badate bene che sono variabili X grande e Y grande, quindi variabili diverse):
Y=\sin x
X=\cos x
Quindi l’equazione goniometrica lineare diventa:
\sqrt{3} Y +3 X +3 = 0
Mettiamo a sistema questa con la prima relazione fondamentale della goniometria:
\cos^2 x + \sin^2 x = 1
Che nelle nuove variabili X e Y diventa:
X^2 + Y^2 = 1
Mettiamo a sistema queste due equazioni, e per risolvere l’esercizio, svolgiamo il sistema seguente quindi:
\begin{cases} \sqrt{3} Y +3 X +3 = 0 \\ X^2 + Y^2 = 1 \end{cases}
SECONDO PUNTO: dalla prima equazione ricaviamo una variabile, ad esempio quella X:
3 X = - \sqrt{3} Y -3
X =- \frac{\sqrt{3}}{3} Y -1
TERZO PUNTO: sostituiamo questo valore di X nella seconda equazione del sistema.
(-\frac{\sqrt{3}}{3} Y -1)^2 + Y^2 = 1
\frac{3}{9}Y^2 +1 + \frac{2 \sqrt{3} }{3} Y + Y^2 = 1
Ora si tratta solo di risolvere questa equazione di secondo grado, quindi portiamo tutto a primo membro e mettiamo in evidenza:
( \frac{1}{3}+1)Y^2 + \frac{2 \sqrt{3} }{3} Y = 0
\frac{4}{3} Y^2 + \frac{2 \sqrt{3} }{3} Y = 0
Moltiplichiamo tutto per 3 per semplificare la forma, inoltre dividiamo per 2 poi:
2 Y^2 + \sqrt{3} Y = 0
Mettiamo in evidenza la Y:
Y(2Y + \sqrt{3} ) = 0
E quindi le due soluzioni Y di questa equazione sono:
Y=0 e poi:
2Y + \sqrt{3} = 0 \implies Y = - \frac{ \sqrt{3} }{2}
A questo punto che abbiamo trovato la Y, passiamo al prossimo punto.
QUARTO PUNTO: Sostituiamo uno per volta la Y nella relazione in X che abbiamo trovato nel secondo punto. E lo facciamo in un sistema:
\begin{cases} Y=0 \\ X =- \frac{\sqrt{3}}{3} Y -1 \end{cases} \implies \begin{cases} Y=0 \\ X =- \frac{\sqrt{3}}{3} \cdotp 0 -1 \end{cases}
\begin{cases} Y=0 \\ X = -1 \end{cases}
E questa è la prima coppia di soluzioni, ricaviamo ora la seconda coppia di soluzioni andando a sostituire questa volta l’altra Y:
\begin{cases} Y=\frac{ \sqrt{3} }{2} \\ X = \frac{\sqrt{3}}{3} Y -1 \end{cases} \implies \begin{cases} Y=\frac{ \sqrt{3} }{2} \\ X = \frac{\sqrt{3}}{3} \frac{ \sqrt{3} }{2} -1 \end{cases}
\begin{cases} Y=\frac{ \sqrt{3} }{2} \\ X = -\frac{1}{2} \end{cases}
QUINTO PUNTO: disegniamo una coppia per volta le due rette in una circonferenza goniometrica e vediamo se intersecano la circonferenza in un angolo comune. Partiamo dalla prima coppia:
\begin{cases} Y=0 \\ X = -1 \end{cases}
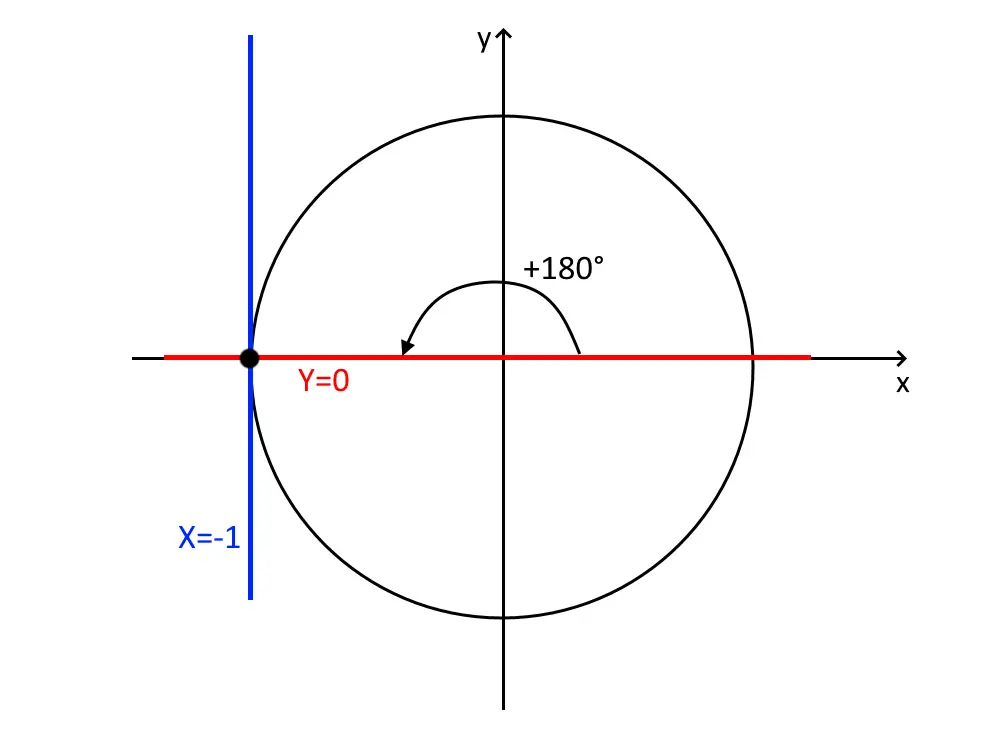
Quell’angolo è chiaramente:
x= \pi + 2k\pi
E questa è la prima soluzione dell’esercizio. Passiamo alla seconda coppia e facciamo lo stesso:
\begin{cases} Y=\frac{ \sqrt{3} }{2} \\ X = -\frac{1}{2} \end{cases}
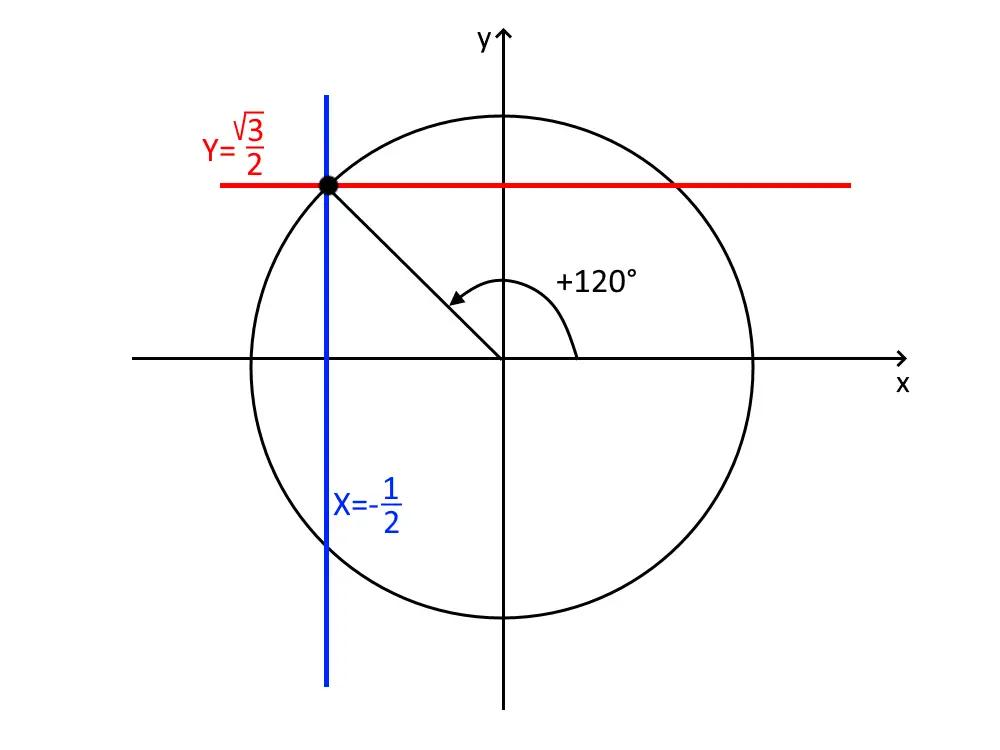
Questo è più difficile da capire, quindi andiamo a vedere sulla calcolatrice mettendo uno dei due valori. Per esempio prendiamo:
X = -\frac{1}{2} \implies \cos x = -\frac{1}{2}
La calcolatrice ci dice:
x=120° = \frac{4}{3} \pi + 2k \pi
L’angolo che ci ha dato la calcolatrice va bene. L’esercizio è concluso.
Esercizio 8. \sqrt{3} \cos x + \sin x - \sqrt{3} = 0
Questo è sempre il caso di una equazione goniometrica lineare non omogenea, ossia della forma:
a \sin x + b \cos x + c= 0
Nell’esercizio precedente abbiamo usato il metodo grafico, adesso utilizzeremo un altro valido metodo: con le formule parametriche. Anche se io vi consiglio il metodo grafico in genere, poi se vedete che le equazioni che escono fuori sono troppo difficili allora provate con questo.
Metodo formule parametriche
Tale metodo richiede una condizione: per usarlo bisogna prima controllare che \pi non sia soluzione. Per vedere basta sostituire alla x il valore di \pi e controllare che non sia verificata l’uguaglianza:
\sqrt{3} \cos \pi + \sin \pi - \sqrt{3} = 0
- \sqrt{3} - \sqrt{3} = 0 \implies - 2\sqrt{3} = 0
Ovviamente il primo membro non è uguale al secondo, e quindi possiamo usare questo metodo!
PRIMO PUNTO: Sostituiamo con le seguenti formule il seno ed il coseno:
\begin{cases} \sin x = \frac{2t}{1+ t^2 } \\ \cos x = \frac{1-t^2}{1+ t^2 } \end{cases}
Dove in pratica queste sono formule tali che t = \tg \frac{x}{2}
L’equazione nostra ora diventa:
\sqrt{3} \frac{1-t^2}{1+ t^2 } + \frac{2t}{1+ t^2 } - \sqrt{3} = 0
Quindi abbiamo trasformato il tutto in una equazione fratta. Il nostro obiettivo ora è trovare la t. Facciamo il minimo comune multiplo:
\frac{\sqrt{3} ( 1 - t^2 ) +2t - \sqrt{3} (1+ t^2) }{1+ t^2 } = 0
\frac{ - 2\sqrt{3} t^2 +2t }{1+ t^2 } = 0
Leviamo il denominatore di mezzo:
- 2\sqrt{3} t^2 +2t = 0
Mettiamo in evidenza 2t:
2t(- \sqrt{3} t +1) = 0
Che ha come soluzioni t=0 e poi:
- \sqrt{3} t +1 = 0 \implies t = \frac{1}{\sqrt{3}} = \frac{ \sqrt{3} }{3}
SECONDO PUNTO: Risostituiamo e torniamo alla x, ricordandoci a cosa era uguale la t:
t = \tg \frac{x}{2}
Quindi una soluzione per volta sostituiamo la t. Partiamo con la prima soluzione t=0:
\tg \frac{x}{2} = 0
Questa la possiamo risolvere per sostituzione, o direttamente diciamo che la tangente è uguale a zero solamente in 0 + k \pi e quindi l’angolo dentro è:
\frac{x}{2} = k \pi
Moltiplichiamo per 2:
x = 2k\pi
E questa è la prima soluzione dell’esercizio. Passiamo a sostituire l’altra t:
\tg \frac{x}{2} = \frac{ \sqrt{3} }{3}
Vediamo sulla calcolatrice che la tangente è uguale a \frac{ \sqrt{3} }{3} in:
\frac{x}{2} = \frac{\pi}{6} + k\pi
x= \frac{\pi}{3} + 2k\pi
La sezione riguardo le equazioni goniometriche lineari in seno e coseno, utilizzando il metodo grafico e le formule parametriche è finito. Adesso trattiamo degli esercizi svolti sulle equazioni goniometriche omogenee di secondo grado.
Equazioni goniometriche di SECONDO GRADO
in seno e coseno
Esercizio 9. - \sqrt{3} \sin^2 x - 2 \sin x \cos x + \sqrt{3} \cos^2 x = 0
Questa è una equazione goniometrica di secondo grado omogenea, ossia della forma:
a \sin^2 x + b \sin x \cos x + c \cos^2 x = 0
In tal caso il procedimento è sempre lo stesso: dividere tutto per \cos^2 x . Le CE (condizioni di esistenza) non servono perché non si può avere in questo caso il denominatore uguale a zero. Quindi dividiamo tutto per il coseno quadro senza pensieri:
- \sqrt{3} \frac{\sin^2 x}{\cos^2 x } - 2 \frac{ \sin x \cos x }{\cos^2 x } + \sqrt{3} \frac{\cos^2 x }{\cos^2 x } = 0
Ricordando la definizione di tangente otteniamo:
- \sqrt{3} \tg^2 x - 2 \tg x + \sqrt{3} = 0
Ossia tutto in termini di tangente, ed essendoci un quadrato presenta, procediamo per sostituzione. Ossia poniamo:
t= \tg x
- \sqrt{3} t^2 - 2 t + \sqrt{3} = 0
E ci siamo ricondotti ad una equazione di secondo grado, cambiamo innanzitutto di segno.
\sqrt{3} t^2 + 2 t - \sqrt{3} = 0
Calcoliamone il delta-quarti:
\frac{\Delta}{4} = (\frac{b}{2})^2 - ac = 1+\sqrt{3}\sqrt{3}=1+3=4
t_{1,2}= \frac{-\frac{b}{2} \pm \sqrt{ \frac{\Delta}{4} } }{a} = \frac{-1 \pm 2 }{ \sqrt{3}}
E quindi le due soluzioni in t sono:
t_1 = \frac{-1 + 2 }{ \sqrt{3}} = \frac{1}{\sqrt{3}} = \frac{\sqrt{3} }{3}
t_2 = \frac{-1 - 2 }{ \sqrt{3} } = - \frac{3}{\sqrt{3} }= - \sqrt{3}
Ritorniamo alla x e concludiamo l’esercizio. Partiamo dalla prima soluzione:
\tg x = \frac{\sqrt{3} }{3}
\implies x= \frac{\pi}{6} + k \pi
E la seconda soluzione è:
\tg x = - \sqrt{3}
\implies x= - \frac{\pi}{3} + k \pi
Esercizio 10. 10 \sin^2 x + 2 \sqrt{3} \sin x \cos x + 4 \cos^2 x = 7
Questa è una equazione goniometrica di secondo grado non omogenea, ossia della forma:
a \sin^2 x + b \sin x \cos x + c \cos^2 x = d
Questa presenta un solo passaggio in più rispetto a quella dell’esercizio precedente omogenea.
Questo passaggio è il seguente:
Visto che 1 = \sin^2 x + \cos^2 x
Allora il numero noto che abbiamo nell’equazione, cioè il 7 lo possiamo scrivere come:
10 \sin^2 x + 2 \sqrt{3} \sin x \cos x + 4 \cos^2 x = 7 \cdotp 1
E quindi:
10 \sin^2 x + 2 \sqrt{3} \sin x \cos x + 4 \cos^2 x = 7 \cdotp (\sin^2 x + \cos^2 x)
Sciogliamo le parentesi:
10 \sin^2 x + 2 \sqrt{3} \sin x \cos x + 4 \cos^2 x = 7\sin^2 x + 7\cos^2 x
E portando tutto a primo membro saremo tornati al caso precedente, ossia dell’equazione omogenea di secondo grado.
10 \sin^2 x + 2 \sqrt{3} \sin x \cos x + 4 \cos^2 x - 7\sin^2 x - 7\cos^2 x =0
3 \sin^2 x + 2 \sqrt{3} \sin x \cos x -3 \cos^2 x =0
E quindi da questo punto in poi seguiamo lo stesso identico procedimento dell’esercizio precedente, e quindi dividiamo tutto per \cos^2 x :
3 \tg^2 x + 2 \sqrt{3} \tg x -3 =0
E come prima, essendoci la presenza di funzioni uguali (tangente) ed un quadrato procediamo per sostituzione. Poniamo:
t = \tg x
3 t^2 + 2 \sqrt{3} t -3 =0
Calcoliamo il delta di questa equazione di secondo grado:
\Delta = b^2 - 4ac = 12+36=48
t_{1,2}= \frac{-b \pm \sqrt{ \Delta } }{2a} = \frac{-2 \sqrt{3} \pm \sqrt{48} }{6}
La radice la scriviamo come:
=\frac{-2 \sqrt{3} \pm \sqrt{16 \cdotp 3 } }{6} =\frac{-2 \sqrt{3} \pm 4\sqrt{ 3 } }{6}
E quindi le due soluzioni sono:
t_1 = \frac{2\sqrt{ 3 } }{6} = \frac{\sqrt{ 3 }}{3}
t_2 = \frac{-6\sqrt{ 3 } }{6} = -\sqrt{ 3 }
A questo punto ritorniamo alla x una soluzione per volta, partendo dalla prima.
\tg x = \frac{\sqrt{ 3 }}{3}
\implies x = \frac{\pi}{6} +k \pi
E poi l’altra:
\tg x = -\sqrt{ 3 }
\implies x =- \frac{\pi}{3} +k \pi
E l’esercizio è concluso!
Abbiamo visto in questa pagina esercizi svolti equazioni goniometriche riconducibili a quelle elementari, esercizi svolti equazioni goniometriche omogenee e non, ed infine abbiam visto esercizi svolti equazioni goniometriche di secondo grado.
Trovate esercizi svolti anche di identità goniometriche, e di equazioni goniometriche elementari.
Continuate a studiare sul nostro sito! Trovate altre centinaia di esercizi svolti di altri argomenti sia di matematica che altro ancora!
Per approfondire:
https://it.wikipedia.org/wiki/Equazione_trigonometrica#:~:text=Un’equazione%20trigonometrica%20o%20goniometrica,quali%20seno%2C%20coseno%20e%20tangente.
Equazioni goniometriche esercizi svolti
goniometriche
elementari
goniometriche
esercizi