Esercizi disequazioni di secondo grado
Esercizi disequazioni di secondo grado: 15 esercizi SVOLTI! Se avete una verifica sulle disequazioni di secondo grado, vi basta una giornata su questa pagina per essere pronti! Prima però, c’è bisogno che sappiate fare o comunque avete una idea di come si fanno le equazioni di secondo grado, altrimenti cliccateci sopra e avrete altri 20 esercizi svolti! Comunque, iniziamo subito mostrandovi l’indice di questa pagina.
Indice
- Formule utili per le disequazioni di secondo grado
- Esercizi disequazioni di secondo grado
- Disequazioni di secondo grado con parametri
- Disequazioni di secondo grado per sostituzione
Iniziamo subito con questa tabella con le formule che ci serviranno per la risoluzione degli esercizi disequazioni di secondo grado!
Formule utili per le disequazioni di secondo grado

Iniziamo subito con gli esercizi disequazioni di secondo grado svolti!
Esercizi disequazioni di secondo grado
Esercizio 1. 2x^2 -5x -3 > 0
Così come per le equazioni di secondo grado, cerchiamo di portare il tutto sempre alla seguente forma.
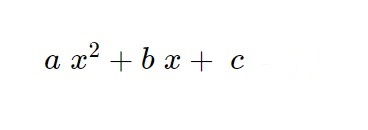
Come potete vedere in questo caso già ce l’abbiamo, e quindi si passa direttamente al calcolo del discriminante. Abbiamo il coefficiente b dispari, e quindi il Delta lo calcoliamo come:
\Delta = b^2 - 4ac = 25+24 = 1
Visto che il discriminante è positivo, e anche la disequazione è con un >, come vedete dalla tabella, allora esiste soluzione; ed il secondo passo è quello di trovare le due soluzioni singole così come per le equazioni di secondo grado:
x_{1,2}= \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{5 \pm 1}{4}
E quindi abbiamo:
x_1 = \frac{5 + 1}{4} = \frac{6}{4} = \frac{3}{2}
x_2 = \frac{5 - 1}{4} = 1
A questo punto c’è la differenza vera e propria con le equazioni di secondo grado. Qui essendoci un maggiore > nella disequazione andiamo a prendere i valori esterni. Cioè andiamo a prendere intervalli di soluzione come:
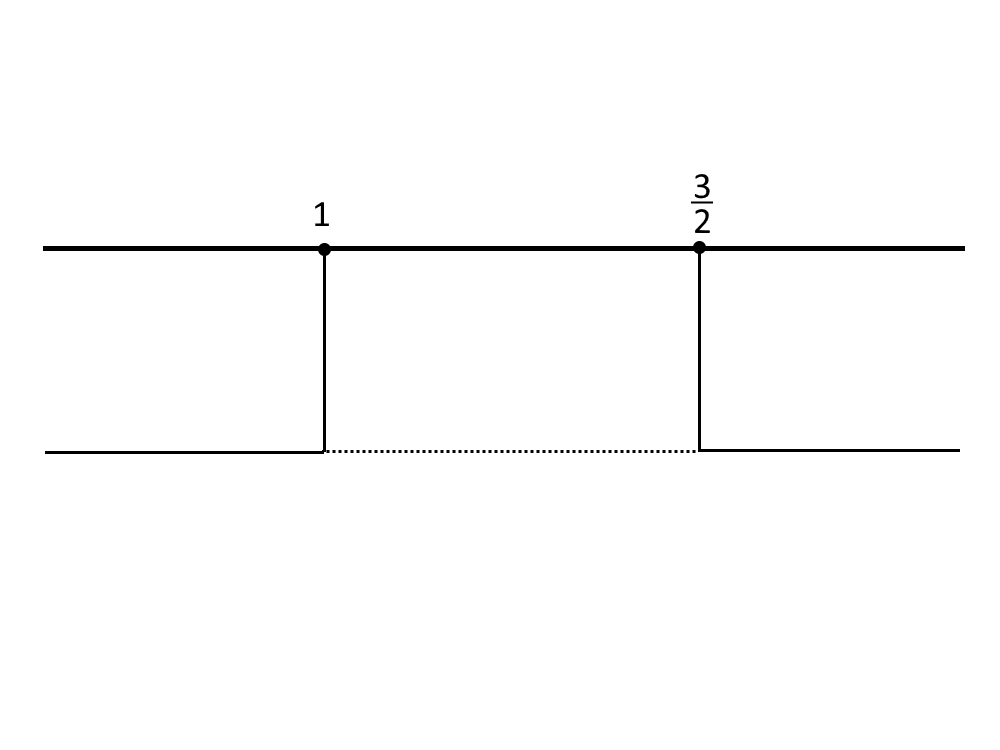
E quindi:
x<1 \lor x > \frac{3}{2}
Esercizio 2. 14 x^2 -7x \ge 0
In questo caso, anche se parzialmente abbiamo la forma di un polinomio di secondo grado, ossia:
ax^2 +bx +c
E quindi possiamo passare al calcolo del discriminante:
\Delta = b^2 - 4ac = 49
Poichè il Delta è positivo, cerchiamo le soluzioni singole, come se fosse una equazione di secondo grado, come fatto prima:
x_{1,2}= \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{7 \pm 7}{28}
E quindi abbiamo:
x_1 = \frac{7 + 7}{28} = \frac{14}{28} = \frac{1}{2}
x_2 = \frac{7 - 7}{28} = 0
A questo punto, essendo la disequazione con un segno \ge e il discriminante positivo, andiamo a prendere i valori esterni. L’unica differenza dell’esercizio precedente è che qui c’è anche un segno di uguale, ma non cambia nulla: semplicemente dovete aggiungere un segno uguale ai valori esterni. Quindi avete in questo caso:
x \le 0 \lor x \ge \frac{1}{2}
E quindi è uguale alla fine dei conti!
Esercizio 3. -3 x^2 -11x - 10 > 0
Così come abbiamo detto tante volte nella risoluzione delle equazioni di secondo grado, nella forma:
ax^2 +bx +c
quando avete il coefficiente a negativo, cambiate sempre tutto di segno! Qui però c’è da stare attenti, perchè quando si cambia tutto di segno una disequazione, bisogna anche cambiare il segno della disequazione! Cioè qui si passa dal > al <!
3 x^2 +11x + 10 < 0
Ora, che c’è un minore non ce ne frega assolutamente nulla: calcoliamo sempre il Delta.
\Delta = b^2 - 4ac = 121-120=1
Abbiamo un Delta positivo, in una disequazione con segno minore: abbiamo sempre soluzione, ma alla fine dei conti prenderemo i valori interni, piuttosto che esterni. Questa è l’unica differenza! Calcoliamo le due soluzioni distinte:
x_{1,2}= \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{-11 \pm 1}{6}
E quindi abbiamo:
x_1 = \frac{-11 + 1}{6} = \frac{-10}{6} = - \frac{5}{3}
x_2 = \frac{-11 - 1}{6} = -\frac{12}{6} = -2
Ed adesso prendiamo i valori interni, perchè abbiamo la disequazione con segno minore!
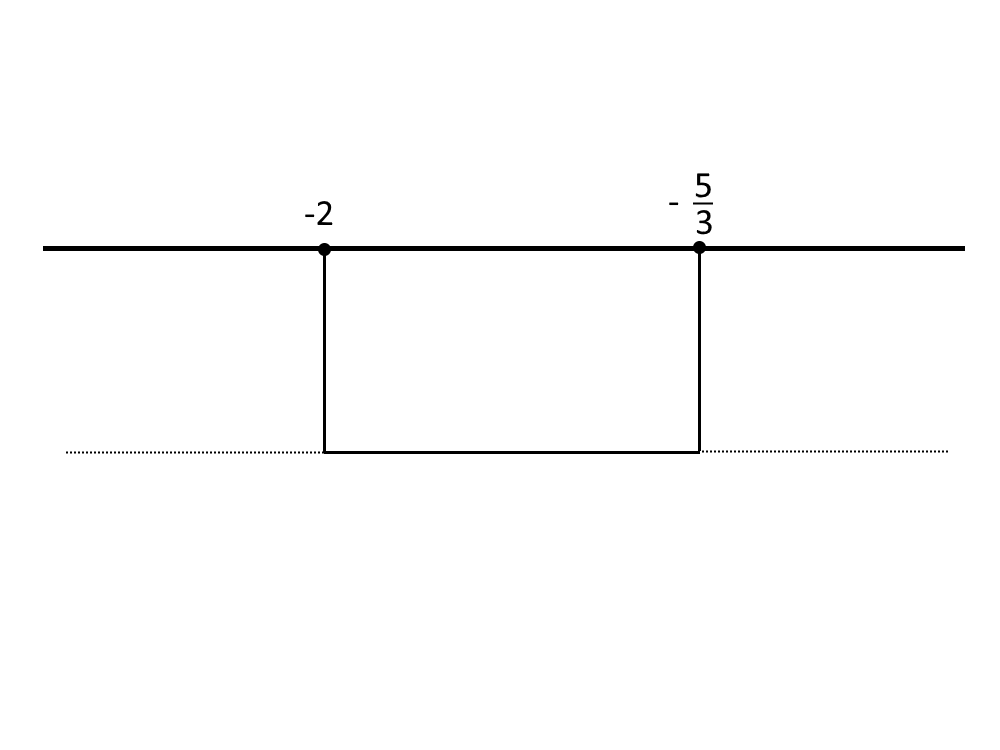
E quindi la soluzione dell’esercizio è:
-2 \le x \le - \frac{5}{3}
Continuiamo con gli esercizi disequazioni di secondo grado svolti!
Esercizio 4. -6x^2 -19x + 20 \ge 0
Notiamo subito che abbiamo il coefficiente a negativo, e quindi cambiamo tutto di segno come prima cosa! E poi ricordatevi di cambiare anche il segno della disequazione, quindi:
6x^2 +19x - 20 \le 0
Come secondo passo sempre la stessa cosa: calcolo del discriminante.
\Delta = b^2 - 4ac = 361+480 = 841
Calcoliamo le due soluzioni distinte, essendoci un Delta positivo:
x_{1,2}= \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{-19 \pm 29}{12}
E quindi si ha:
x_1 = \frac{-19 + 29}{12} = \frac{10}{12} = \frac{5}{6}
x_2 = \frac{-19 - 29}{12} = -\frac{48}{12} = -4
E visto che abbiamo una disequazione con segno minore prendiamo valori interni, chiaramente aggiungendo un segno uguale, visto che abbiamo un \le . La soluzione dell’esercizio è:
-4 \le x \le - \frac{5}{6}
Esercizio 5. 2x^2 + 20x +50 \ge 0
Come prima cosa calcoliamo come sempre il discriminante. In questo caso il coefficiente b del polinomio di secondo grado è pari, e quindi usiamo la formula del Delta/quarti:
\frac{\Delta}{4} = (\frac{b}{2})^2 -ac = 100 - 100= 0
Qui rientriamo per la prima volta nel caso in cui il discriminante è 0.
Il secondo passo da fare in questo caso, e ogni volta che avremo un discriminante nullo, è quello di scrivere la disequazione nel modo seguente:
(x - x_1 )^2 \ge 0
Dove x_1 sarebbe la soluzione, calcolata come se fosse una semplice equazione. Quindi usando la solita formula seguente, dove però ricordiamo che le soluzioni sono coincidenti.
x_{1,2}= \frac{-\frac{b}{2} \pm \sqrt{\frac{\Delta}{4} } }{a} = \frac{-10}{2}=-5
E quindi la nostra disequazione diventa:
(x - x_1 )^2 \ge 0
(x - (-5) )^2 \ge 0
(x +5 )^2 \ge 0
Notiamo che (x +5 )^2 è uguale a zero per x=-5, ed è positivo sempre per qualsiasi x, essendo un quadrato. Quindi \forall x \in \Reals esso è maggiore o uguale a zero. E quindi la disequazione è soddisfatta per qualsiasi valore di x!
Esercizio 6. x^2 +2x +1 > 0
Primo punto: calcoliamo il discriminante.
\frac{\Delta}{4} = (\frac{b}{2})^2 -ac = 1 - 1= 0
Abbiamo discriminante nullo. Quindi come fatto prima, riduciamo la disequazione alla forma seguente. Questa volta con un segno > perchè bisogna mettere lo stesso segno della disequazione chiaramente.
(x - x_1 )^2 > 0
Quindi calcoliamo:
x_{1,2}= \frac{-\frac{b}{2} \pm \sqrt{\frac{\Delta}{4} } }{a} = \frac{-1}{1}=-1
E quindi la nostra disequazione diventa:
(x -(-1) )^2 > 0
(x +1 )^2 > 0
Ora, essendo un quadrato allora è sicuramente positivo \forall x . Però notiamo che se x=-1 esso diventa zero. E questo non va bene perchè la disequazione vuole solamente che sia >0. Quindi prendiamo tutti i valori tranne questo. Quindi:
\forall x \ne -1
Come vedete questi a discriminante nullo sono più a ragionamento!
Esercizio 7. -x^2 +7x - \frac{49}{4} \ge 0
Qui visto che abbiamo il coefficiente a negativo, cambiamo tutto di segno!
x^2 - 7x + \frac{49}{4} \le 0
Dopo di che siamo pronti per il calcolo del Delta:
\Delta = b^2 - 4ac = 49 - 49 = 0
Calcoliamo la soluzione riconducendoci sempre alla stessa forma di prima.
x_{1,2}= \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{7 }{2}
E quindi la nostra disequazione diventa:
(x - \frac{7 }{2} )^2 \le 0
Ora notiamo che essendo un quadrato questo è sicuramente positivo, però la disequazione vuole trovare le x tale che il quadrato sia \le 0 . Un quadrato minore di zero è impossibile, non c’è. Al massimo esso può essere uguale a zero, e questo ci vabene perchè il segno della disequazione lo comprende. E quindi l’unica soluzione che prendiamo è proprio quella per il quale esso fa zero, ossia:
x = \frac{7 }{2}
Continuiamo con gli esercizi disequazioni di secondo grado svolti!
Esercizio 8. 3a^2 -12a +12 \le 0
Quando avete una incognita diversa dalla x poco importa, è la stessa cosa ma con un nome diverso! Qui attenzione, non c’è nessun parametro, perchè avete solo una incognita a.
Calcoliamo il Delta:
\frac{\Delta}{4} = (\frac{b}{2})^2 -ac = 36 - 36= 0
Abbiamo discriminante nullo, quindi sempre stesso procedimento: riconduciamoci alla forma seguente.
(a-a_1)^2 \le 0
Per far ciò calcoliamo la soluzione come se fosse una equazione:
a_{1,2}= \frac{-\frac{b}{2} \pm \sqrt{\frac{\Delta}{4} } }{a} = \frac{6}{3}=2
La nostra disequazione diventa quindi:
(a-2)^2 \le 0
Visto che un quadrato non è mai minore di zero, quindi questa non è mai <0. Però sicuramente può essere =0 chiaramente se a=2. Ricordatevi che noi andiamo a prendere anche l’uguale perchè è contenuto nel segno della disequazione (\le ).
Quindi prendiamo come soluzione solamente a=2.
Esercizio 9. x^2 +4x +7 \ge 0
Calcoliamo il discriminante come prima cosa:
\frac{\Delta}{4} = (\frac{b}{2})^2 -ac = 4 - 7= -3
Qui abbiamo per la prima volta un discriminante negativo <0. Questi sono i più semplici perchè basta imparare a memoria la tabella. Di fatti non c’è bisogno di fare nessun tipo di calcolo. Vediamo che con Delta<0 e con la disequazione con il segno di maggiore (o uguale) \ge allora la soluzione è:
\forall x \in \Reals
Chiaramente state semplicemente attenti al fatto che: il segno della disequazione giusto è quello quando il coefficiente a risulta positivo ovviamente.
ax^2 +bx + c
Altrimenti bisogna prima cambiare tutto di segno, non dimenticatevelo!
Esercizio 10. -x^2 -3x -7 < 0
Per esempio qui, il vero segno della disequazione non è <, perchè bisogna prima ricondurci ad avere un coefficiente a positivo, quindi cambiamo tutto di segno prima!
x^2 +3x +7 > 0
Adesso possiamo calcolare il Delta e trarne le giuste conclusioni:
\Delta = b^2 - 4ac = 9 - 28 = -19
Qui risulta essere un discriminante negativo <0, e con un segno della disequazione di maggiore (>), e quando c’è il maggiore come prima la soluzione è:
\forall x \in \Reals
Senza fare nessun calcolo, ci piacciono!
Abbiamo detto che se c’è Delta<0 e disequazione con segno di maggiore la soluzione è: tutte le x. E cosa succede quando abbiamo Delta<0 e disequazione invece con un minore? Adesso lo vediamo nel prossimo esercizio!
Esercizio 11. 10x^2 -9x +5 \le 0
Calcoliamo il Delta della disequazione di secondo grado innanzitutto e ci accorgiamo che:
\Delta = b^2 - 4ac = 81 - 100 = -19
Delta<0 e questa volta con il segno della disequazione di minore (o uguale) e vedendo nella tabella, anche qui senza fare nessun calcolo, notiamo che la soluzione è:
impossibile.
Quando una disequazione è impossibile? Trovate la risposta su disequazioni impossibili.
Notiamo che per quanto riguarda il Delta<0 non importa se c’è l’uguale o meno per il risultato!
Continuiamo con gli esercizi disequazioni di secondo grado svolti!
Disequazioni di secondo grado con parametri
Esercizio 12. 2x^2 -5ax -3a^2 \le 0
I modi di procedere con i parametri sono principalmente due: il primo è quando affianco al termine quadratico x^2 non abbiamo nessun parametro, come qui; e la prima cosa da fare in tal caso è calcolare il Delta semplicemente, usando sempre la formula del coefficiente b dispari, perchè non siamo sicuri del fatto che sia dispari o pari.
\Delta = b^2 - 4ac = 25a^2 + 24a^2 = 49 a^2
Ricordatevi di trattare i parametri come fossero normali numeri!
Adesso inizia la discussione vera e propria. A seconda del valore del parametro a possiamo avere delta diversi.
Partiamo dal Delta=0, lo possiamo avere? Sì, se a=0 segue che 49 a^2 = 49 \cdotp 0 = 0
- Quindi se a=0
abbiamo Delta nullo, e sostituendo nella disequazione questo valore di a, essa diventa:
2x^2 \le 0
Questo, essendo un quadrato, è sempre positivo, o al massimo può essere uguale a zero se x=0. Questa disequazione è soddisfatta proprio per quest’ultimo valore x=0.
Quindi, ricapitolando, se a=0 segue che la soluzione è x=0.
- Se a>0
allora il delta è chiaramente positivo. Quindi andiamoci a calcolare le due soluzioni singole, proprio come fatto per una semplice disequazione nei primi esercizi!
x_{1,2}= \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{5a \pm \sqrt{49 a^2} }{4} = \frac{5a \pm 7a }{4}
E quindi abbiamo:
x_1 = \frac{5a + 7a}{4}= \frac{12a }{4} = 3a
x_2 = \frac{5a - 7a }{4} = \frac{-2a }{4} = -\frac{a}{2}
Il segno della disequazione è un minore o uguale e quindi prendiamo i valori interni di questi valori!
La soluzione quindi per a>0 è:
-\frac{a}{2} \le x \le 3a
- Se a<0
allora il Delta è comunque positivo ed è lo stesso identico. Anche le soluzioni sono le stesse e viene tutto uguale! Però essendo che ora a<0 il risultato finale è inverso:
3a \le x \le -\frac{a}{2}
Perchè ora è 3a ad essere negativo, essendo a<0!
Esercizio 13. a^2 x^2 +5ax +6 \ge 0
Ora invece abbiamo il secondo caso: quello in cui di fianco al termine quadratico x^2 c’è un parametro. In questi casi l’unica discussione in più è la seguente.
Se a=0 segue che la disequazione non è più di secondo grado e diventa:
6 \ge 0
Ed è chiaro che 6 è sempre maggiore o uguale a zero, per qualsiasi x ovviamente.
Quindi se a=0 allora la soluzione è \forall x .
Ora consideriamo l’altro insieme di casi in cui a \ne 0 . Da qui in poi il procedimento e l’esercizio è il medesimo, calcoliamo il discriminante:
\Delta = b^2 - 4ac = 25a^2 - 24a^2 = a^2
Ora distinguiamo due casi.
- Se a>0
Il Delta è sempre positivo e quindi ci andiamo a calcolare le due soluzioni distinte:
x_{1,2}= \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{-5a \pm a }{2a^2}
E quindi segue che:
x_1 = \frac{-5a + a }{2a^2} =- \frac{2 }{a}
x_2 = \frac{-5a - a }{2a^2} = - \frac{3 }{a}
Visto che la disequazione è con un segno di maggiore o uguale, prendiamo i valori esterni di queste due singole soluzioni. Quindi abbiamo che:
x \le - \frac{3 }{a} \lor x \ge - \frac{2 }{a}
- Se a<0
Qui il delta è sempre lo stesso, ma cambiamo i segni delle due soluzioni singole, ed invertiamo semplicemente la soluzione precedente. Qui abbiamo invece che:
x \le - \frac{2 }{a} \lor x \ge - \frac{3 }{a}
E la discussione è completata!
Continuiamo con gli esercizi disequazioni di secondo grado svolti!
Disequazioni di secondo grado per sostituzione
Esercizio 14. - x^4 +x^2 +2 > 0
In tali casi, quando avete un termine alla quarta ed uno alla seconda, si procede per sostituzione. Poniamo infatti:
t=x^2
E quindi la disequazione diventa:
- t^2 +t +2 > 0
E la disequazione è diventata una classica, che sappiamo risolvere! Di fatti cambiamo innanzitutto di segno tutto.
t^2 - t - 2 < 0
Calcoliamo il discriminante.
\Delta = b^2 - 4ac = 1 +8 = 9
Delta positivo, e quindi andiamo a calcolare le due soluzioni distinte.
t_{1,2}= \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{1 \pm 3 }{2}
E quindi segue che:
t_1 = \frac{1 + 3 }{2} = 2
t_2 = \frac{1 - 3 }{2} = - 1
Ricordatevi chiaramente che queste sono le soluzioni in t e non in x !
E visto che la disequazione è con un segno di maggiore, andiamo a prendere i valori esterni!
t < - 1 \lor t > 2
A questo punto, e solo a questo punto, andiamo a risostituire!
Abbiamo quindi:
x^2 < - 1 \lor x^2 > 2
E ce le calcoliamo separatamente.
x^2 < - 1
Qui abbiamo un quadrato che è sempre positivo, e quindi non è mai minore di -1!
Qua la soluzione è impossibile. Passiamo alla prossima:
x^2 > 2
Facciamo la radice ad entrambi i membri, e visto il maggiore prendiamo i valori esterni! La soluzione è:
x < - \sqrt{2} \lor x > \sqrt{2}
Ed è anche la soluzione dell’esercizio intero!
Esercizio 15. (2-x^2 )^2 < 4
Iniziamo a risolvere il quadrato del binomio, utilizzando la classica formula:
(a+b)^2 = a^2 + 2ab + b^2
E quindi nel nostro caso diventa:
4 + x^4 -4x^2 < 4
Portando poi il 4 a primo membro otteniamo:
4 + x^4 -4x^2 -4 < 0
x^4 -4x^2 < 0
Ora la disequazione la si può svolgere direttamente mettendo in evidenza la x^2 o procedendo per sostituzione e calcolando il discriminante. Noi vogliamo far vedere come procedere per sostituzione e quindi poniamo:
t=x^2
La disequazione nella nuova variabile diventa:
t^2 -4t < 0
Che è una disequazione di secondo grado in cui il coefficiente c=0, ma comunque che sappiamo risolvere! Calcoliamo il discriminante:
\frac{\Delta}{4} = (\frac{b}{2})^2 -ac = 4 - 0= 4
Delta>0 con un segno di minore, e quindi calcoliamo come detto nei primi esercizi le due distinte soluzioni:
x_{1,2}= \frac{-\frac{b}{2} \pm \sqrt{\frac{\Delta}{4} } }{a} = 2 \pm 2
Ed abbiamo:
x_1 = 2+2=4
x_2 = 2-2=0
E visto che il segno della disequazione è un minore, andiamo a prendere i valori interni:
0 < t < 4
A questo punto dobbiamo ritornare alla variabile x iniziale, quindi risostituiamo:
0 < x^2 < 4
Abbiamo ora due piccole disequazioni che risolviamo in maniera distinta (e che vi consiglio sempre di fare) :
0 < x^2
Ossia:
x^2 >0
Questa prima disequazione è veritiera per ogni x diverso da zero, perchè un quadrato è sempre positivo, ma nel caso in cui la x fosse uguale a zero, allora la disequazione non risulterebbe soddisfatta. Quindi prendiamo da questa:
x \ne 0
Passiamo alla seconda disequazione:
x^2 < 4
Questa la si risolve facilmente applicando la radice e quindi abbiamo le soluzioni distinte \pm 2 , ed a queste prendiamo i valori interni, essendoci un minore, quindi:
-2 < x <2
Unendo anche l’altra soluzione, escludiamo lo zero, ed otteniamo che la soluzione dell’esercizio è:
-2 < x <0 \lor 0<x<2
In questa pagina abbiamo visto tanti esercizi per disequazioni di secondo grado. Sarete pronti per la verifica! Vi invito, se avete dubbi ancora a vedere anche gli esercizi sulle equazioni di secondo grado. Continuate a studiare nel nostro sito con altre centinaia di esercizi di matematica che altro ancora!
Per approfondire:
https://it.wikipedia.org/wiki/Disequazione_quadratica
secondo
grado
disequazione
impossibile?