Quando una disequazione è impossibile?
Quando una disequazione è impossibile? Una disequazione può avere come soluzione “impossibile” solamente in particolari casi. In questa pagina vedremo sia il caso della soluzione “impossibile” nelle disequazioni di primo grado che quello nelle disequazioni di secondo grado.
Indice
Iniziamo subito a vedere quando può capitare, nelle disequazioni di primo grado, che esca fuori come soluzione impossibile.
Disequazioni di primo grado impossibili
La tattica migliore per capire una cosa è vedere degli esempi ed esercizi svolti: andiamo subito al dunque!
Esercizio 1. 3(x+5) \le 2(x+2) - (3-x)
Per vedere che soluzione ha, dobbiamo risolverla. Come sappiamo, il primo passo da effettuare quando si ha di fronte una disequazione, è di levarci da mezzo le parentesi tonde che compaiono. Di conseguenza andiamo ad effettuare la moltiplicazione dei vari termini davanti alle parentesi. (Ricordate che un segno meno davanti ad una parentesi cambia di segno tutti i termini all’interno della stessa):
3x+15 \le 2x+4 - 3+x
Poi, come seconda cosa: portiamo tutte le x a primo membro ( a sinistra) ed il resto a secondo membro. Ricordate di cambiare segno quando fate passare un termine da una parte all’altra!
3x-2x-x \le -15+4 - 3
0x \le -14
Come vedete abbiamo uno zero come coefficiente della x, ossia che moltiplica la x. Adesso dobbiamo verificare che tipo di soluzione è. Per qualsiasi x, uno zero che moltiplica qualcosa dà sempre zero. Quindi, noi avremo sempre:
0 \le -14
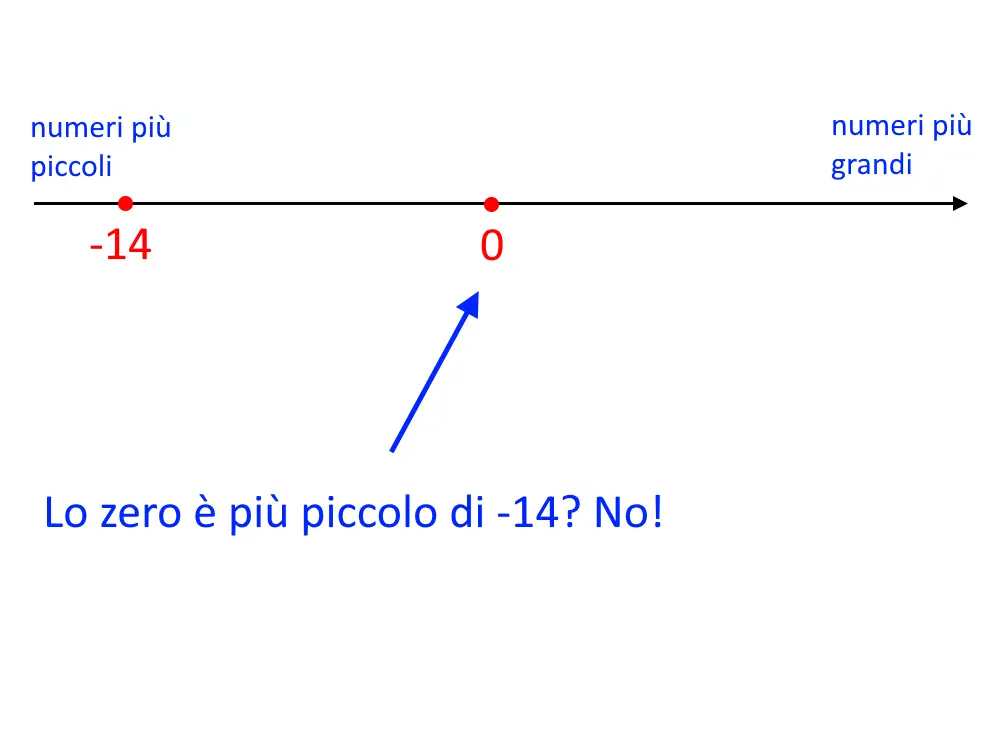
Adesso dobbiamo chiederci: lo 0 è più piccolo o uguale di -14? Chiaramente la risposta è no! Lo zero è più grande di -14, quindi tale disequazione non sarà MAI verificata. Si dirà quindi che la soluzione è impossibile!
Esercizio 2. 8-4x - 5(1-3x) > 12x + 6 - x
Anche qui, come sempre, risolviamo dapprima quella parentesi:
8-4x - 5+15x > 12x + 6 - x
Portiamo le variabili x a sinistra, ed il restante a destra:
-4x +15x -12x+x> + 6 +5-8
Sommiamo i rispettivi termini simili:
0x > 3
Questo è sempre il caso di avere uno zero attaccato alla x. Per qualsiasi x questo è sempre:
0 > 3
La domanda che ci dobbiamo porgere, leggendo la disequazione, è: lo zero è più grande (>) di 3? La risposta è no. Lo zero è più piccolo di 3, quindi la disequazione non è mai verificata, e la soluzione dunque è impossibile.
NON CONFONDETEVI: non sempre una forma del tipo 0x > k porta ad una soluzione impossibile. Di fatti se abbiamo:
0x < 20
Significa che per qualsiasi x questo è equivalente a:
0 < 20
Ora ci poniamo la domanda: 0 è più piccolo di 20? Beh, in questo caso sì! Quindi la soluzione è:
\forall x
L’importante è porsi quella domanda, poi la soluzione verrà da sé!
Vediamo ora quando quando una disequazione di secondo grado è impossibile!
Quando una disequazione di secondo grado è impossibile?
Possiamo avere, da una disequazione di secondo grado, come soluzione impossibile, solo in due casi.
- \Delta = 0 in una disequazione col segno di minore (<);
- \Delta < 0 in una disequazione col segno di minore o minore uguale (< oppure \le );
Questo lo potete osservare bene dalla tabella seguente.

Per capire meglio, vediamo diversi esercizi svolti e spiegati con calma di questi due casi.
Disequazioni impossibili con
\Delta = 0
Esercizio 3. -2x^2 -3x - \frac{9}{8} > 0
Se non ricordate come si risolve una disequazione di secondo grado, vi invito a cliccarci su. Sicuramente notiamo che il coefficiente a è negativo e quindi cambiamo tutto di segno:
2x^2 +3x + \frac{9}{8} < 0
A questo punto, visto che la disequazione è ordinata, calcoliamo il delta:
\Delta = b^2 - 4ac = 9 - 4 \cdotp 2 \cdotp \frac{9}{8} = 9-9 = 0
Viene fuori che il delta=0, e noi siamo in una disequazione col segno di minore (<). Di conseguenza vediamo in tabella in che caso siamo! Siamo nel caso in cui la disequazione ha direttamente come soluzione impossibile. Non c’è nessun altro calcolo da fare.
Come vedete qui basta semplicemente ricordarsi di tale specifico caso.
Esercizio 4. \frac{x^2}{5} -2x +5 < 0
Calcoliamo direttamente il delta-quarti questa volta (visto che il coefficiente b è pari):
\frac{\Delta }{4} = (\frac{b}{2})^2 - ac = 1 - \frac{1}{5}5 = 1-1 = 0
Delta è nullo, e siamo nel caso in cui la disequazione è minore. Vediamo nella tabella…è lo stesso caso di prima, in cui non vi è necessità di fare ulteriori calcoli. Questo perché la soluzione della disequazione è impossibile.
Disequazioni impossibili con
\Delta < 0
Esercizio 5. 40 + x^2 -x < 0
Riordiniamola prima, per far figurare meglio i coefficienti della formula del discriminante.
x^2 -x +40 < 0
A questo punto:
\Delta = b^2 - 4ac = 1 - 4 \cdotp 40 = 1-160 = -159
Delta<0, e siamo in una disequazione in cui vi è un segno di minore: di conseguenza la soluzione è impossibile. Ossia non è possibili risolverla!
Come vedete è anche meglio che venga come soluzione impossibile, così ci sono meno calcoli da fare!
Esercizio 6. - x^2 +6x -11 \ge 0
Il coefficiente della x quadratica è con un segno meno, quindi cambiamo innanzitutto di segno tutto (ricordate di cambiare anche il segno stesso della disequazione).
x^2 -6x + 11 \le 0
Siamo pronti per trovare il Delta-quarti!
\frac{\Delta }{4} = (\frac{b}{2})^2 - ac = 9 - 11 = -2
Delta<0, ed il segno è di minore o uguale (\le )…ottimo perché non dobbiamo fare nessun calcolo! Tale disequazione è impossibile o non ha soluzione!
In questa pagina abbiamo visto quando una disequazione è impossibile. In particolare può capitare per una disequazione di primo grado, e in due casi per le disequazioni di secondo grado! Potete continuare a studiare sul nostro sito!
Trovate sul nostro sito centinaia di esercizi svolti sia di matematica che di geometria e geometria analitica!
Per approfondire:
https://it.wikipedia.org/wiki/Disequazione
di 2° grado
esercizi
valore
assoluto