Esercizi SVOLTI limiti: 30 ESERCIZI sui LIMITI!
Esercizi SVOLTI limiti: 30 ESERCIZI sui LIMITI! In questa pagina vedremo le proprietà fondamentali del calcolo dei limiti, svolgeremo 30 esercizi spiegati con cura e passo dopo passo. Ci saranno varie difficoltà: facile, medio e difficile, anche se in generale questi limiti sono calcoli base, quindi abbastanza semplici. Per le forme indeterminate e i limiti notevoli che sono più complicate invece, ci sono pagine apposite solamente per questi tipi di limiti! Cliccateci sopra!
Indice
- Proprietà dei limiti
- Esercizi sui limiti semplici
- Limite con x che tende ad infinito
- Esercizi sui limiti difficoltà media
- Esercizi svolti limiti difficili
- Calcolo con il Teorema del CONFRONTO
- Come risolvere i limiti, consigli
Iniziamo subito col calcolo dei limiti!
Proprietà dei limiti

Iniziamo subito!
Esercizi sui limiti semplici
Esercizio 1. \lim\limits_{x\to e } (3-\ln x)
Il limite è formato da due pezzi. Possiamo quindi innanzitutto suddividerlo in due limiti più semplici, usando la proprietà 2. Ci dobbiamo sempre semplificare la vita prima di fare qualche calcolo!
\lim\limits_{x\to e } (3-\ln x) =\lim\limits_{x\to e } 3 + \lim\limits_{x\to e } (-\ln x)
Il meno del secondo termine lo possiamo portare fuori, perchè è una costante (-1). Quindi viene:
= \lim\limits_{x\to e } 3 - \lim\limits_{x\to e } \ln x
Il primo limite non contiene nessuna x, quindi la x non può tendere da nessuna parte! La costante 3 rimane sempre la costante 3, perchè non c’è nessuna funzione con la variabile x! Quindi il limite fa semplicemente 3!
=3 - \lim\limits_{x\to e } \ln x
Il secondo limite invece, la x ce l’ha e come! Il limite di x che tende ad e significa che la x va nel punto x=e e quindi bisogna come sempre nei limiti sostituire al posto della x il punto nella quale tende, quindi x=e in questo caso!
=3 - \lim\limits_{x\to e } \ln x =3 - \ln e = 3-1= 2
Esercizio 2. \lim\limits_{x\to -4 } e^{\frac{-4}{x}}
Qui abbiamo un solo limite, con una sola x, è semplice! Basta sostituire alla x il punto nella quale tende, quindi il -4. Il limite è immediato:
\lim\limits_{x\to -4 } e^{\frac{-4}{x}} = e^{\frac{-4}{-4}} = e^1 = e
IMPORTANTE! Non vi dimenticate mai di scrivere il simbolo del limite, altrimenti è errore! Quando invece sostituite la x nella funzione lì non bisogna più metterlo ovviamente, perchè già avete effettuato il limite.
Cosa significa fare il LIMITE? In generale il limite di una funzione è:
\lim\limits_{x\to x_0} f(x) =f(x_0)
In pratica noi abbiamo una funzione f(x) definita in un dominio sull’asse x. Effettuare un limite significa portare una coordinata x che va verso il punto dell’ascisse x_0 partendo da un’intorno di tale punto. Cioè partiamo con la x vicino ad x_0 e poi in corrispondenza di x_0 ci sarà la funzione che avrà il valore f(x_0 )! Questo significa effettuare il limite.
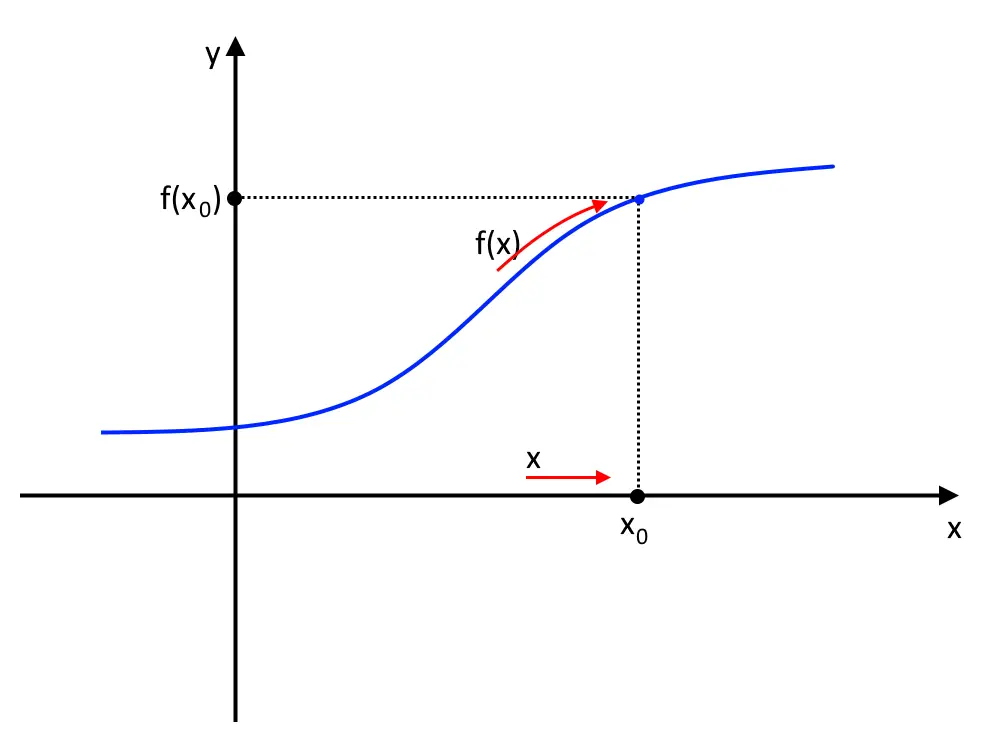
Esercizio 3. \lim\limits_{x\to -1^+} \frac{1}{x+1}
Il limite non ha somma nè prodotti nè costanti da portare fuori. Dobbiamo solamente sostituire la x alla quale tende. Prima di andare avanti cerchiamo un attimo di capire cosa significa -1^+.
Facciamo un passetto alla volta, partiamo da -1. A questo punto come vediamo c’è un segno + che aggiunge un piccolissimo valore positivo al -1. Quindi diventa:
-1+0,0000001=-0,9999999
Ritorniamo all’esercizio, andiamo a sositutire:
\lim\limits_{x\to -1^+} \frac{1}{x+1} =\frac{1}{-1^+ +1}
Concentriamoci sul denominatore per vedere quanto fa quella cosa strana, che in realtà difficile non è!
-1^+ +1 = -0,9999... + 1 = +0,000000.....00001 = 0^+
Ossia uno zero un pochetto più grande di zero.
Torniamo all’esercizio.
\frac{1}{-1^+ +1} =\frac{1}{0^+} =+ \infin vedendo nella tabella.
Continuiamo con gli esercizi svolti sui limiti!
Esercizio 4. \lim\limits_{x\to - 1 } \frac{-5}{(x+1)^2}
Anche qui non c’è bisogno di fare nulla! Sostituiamo e basta.
\lim\limits_{x\to - 1 } \frac{-5}{(x+1)^2} = \frac{-5}{(-1+1)^2}
Chiaramente -1+1=0. E zero elevato al quadrato fa sempre zero, quindi abbiamo:
= \frac{-5}{0}
Basta vedere adesso in tabella che un qualsiasi numero diviso per zero fa infinito, però abbiamo un segno meno, quindi fa meno infinito!
= \frac{-5}{0} =- \infin
Vediamo altri esercizi sui limiti semplici!
Esercizio 5. \lim\limits_{x\to 0^+ } (\frac{2x^2 + x}{2x+5} + \frac{1}{\sin x})
Non facciamoci spaventare! Un passo alla volta. Abbiamo una somma: spezziamo il limite in due con la proprietà 2.
\lim\limits_{x\to 0^+ } (\frac{2x^2 + x}{2x+5} + \frac{1}{\sin x}) =\lim\limits_{x\to 0^+ } \frac{2x^2 + x}{2x+5} +\lim\limits_{x\to 0^+ } \frac{1}{\sin x}
Risolviamone uno alla volta, non complichiamoci le cose! Partiamo dal secondo che sembra più semplice.
\lim\limits_{x\to 0^+ } \frac{1}{\sin x}
Come detto prima, quando abbiamo una qualsiasi funzione, dobbiamo vedere il grafico. Qui abbiamo il \sin x, il cui grafico è:
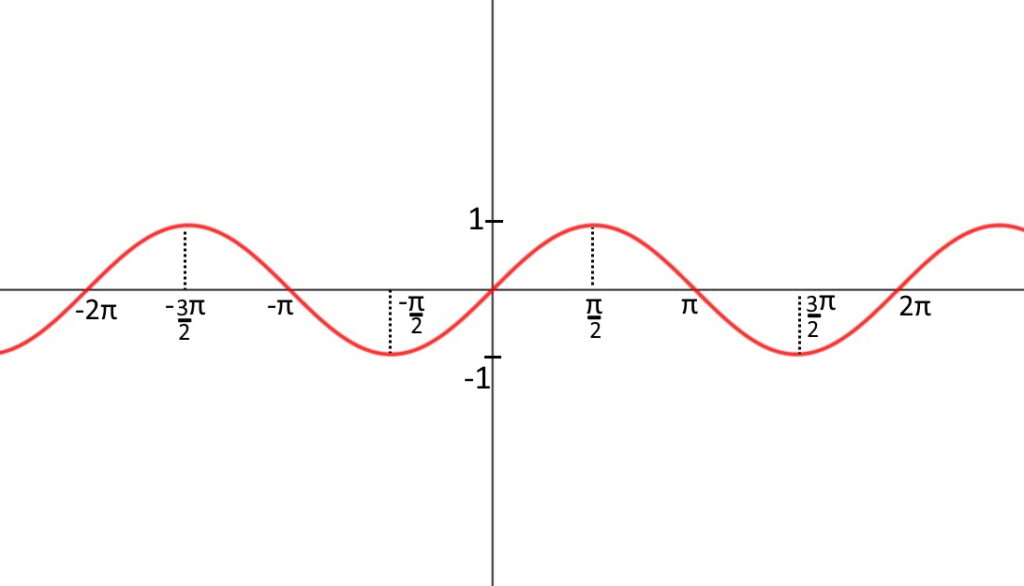
Come possiamo vedere nel punto dell’ascisse 0^+, cioè uno zero leggermente più grande, vediamo che la funzione seno è anch’essa uno zero leggermente più grande. Quindi:
\lim\limits_{x\to 0^+ } \frac{1}{\sin x} = \frac{1}{\sin 0^+} = \frac{1}{0^+} =+ \infin
vedendo sempre nella tabella da imparare a memoria! Il secondo limite l’abbiamo risolto, vediamo adesso il primo:
\lim\limits_{x\to 0^+ } \frac{2x^2 + x}{2x+5}
Sostituiamo semplicemente, senza nessun passaggio. Quando siete dubbiosi, sostituite e se vedete che vengono cose troppo complicate che non sapete fare, allora ci voleva qualche passaggio prima: cose che vedremo negli esercizi un po’ più difficili.
\lim\limits_{x\to 0^+ } \frac{2x^2 + x}{2x+5} = \frac{2(0^+ )^2 + 0^+}{2\cdotp 0^+ +5} =
Un numero moltiplicato per zero fa sempre zero. Zero sommato a 5 fa sempre 5.
Quindi viene:
\frac{2(0^+ )^2 + 0^+}{2\cdotp 0^+ +5} = \frac{0+0}{0+5}=\frac{0}{5}= 0
Sommiamo anche il risultato dell’altro limite ed otteniamo:
=0 + \infin =+ \infin
Quando scrivere precisamente 5^{\pm}? Questi non si scrivono quasi mai negli esercizi. Si mettono solo quando sono fondamentali per capirne il segno del limite! Quindi per esempio in \lim\limits_{x\to 0^+ } \frac{1}{x} è fondamentale metterlo, perchè scrivere:
\lim\limits_{x\to 0^+ } \frac{1}{x} = \frac{1}{0^+}=+\infin ci permette di capire esattamente che il segno dell’infinito è positivo. Invece guardate qui in quest’altro esempio:
\lim\limits_{x\to 0^+ } 5 +x =5 + 0^+ = 5
Ora scrivere 5 o 5^+ è la stessa cosa, sempre 5 è! Se proprio volete essere precisissimi scrivetelo anche, è uguale! Ma comunque non è necessario.
Esercizio 6. \lim\limits_{x\to 2} \frac{3^x - 2^x}{4^{2x} - 4^x -20}
Sostituiamo, non sembrano esserci problemi. Vi ricordo che se sostituite e come vedremo nelle forme indeterminate dei limiti ci sono dei problemi a trovare una soluzione, allora bisogna fare prima qualche passaggio che vedremo.
Qui nessun problema!
\lim\limits_{x\to 2} \frac{3^x - 2^x}{4^{2x} - 4^x -20} = \frac{3^2 - 2^2}{4^{2\cdotp 2} - 4^2 -20} =
= \frac{9 - 4}{256 - 16 -20} = \frac{5}{220} = \frac{1}{44}
ed è finito!
Esercizio 7. \lim\limits_{x\to 4^+} \frac{\log_2 x +1}{3 \log_4 x -3}
Qui, bisogna ricordarci di una cosa. Quando abbiamo il logaritmo in base 4 per esempio, \log_4 4 = 1 così come con \log_6 6 = 1, cioè quando il logaritmo ha base e argomento uguali fa 1. Nell’esercizio ciò che ci interessa particolarmente è al denominatore dopo che sostituiamo:
\lim\limits_{x\to 4^+} \frac{\log_2 x +1}{3 \log_4 x -3} = \frac{\log_2 4^+ +1}{3 \log_4 4^+ -3}
Quanto fa \log_4 4^+?
Abbiamo detto che \log_4 4 = 1 e visto che il logaritmo è una funzione crescente, come potete vedere dal grafico:
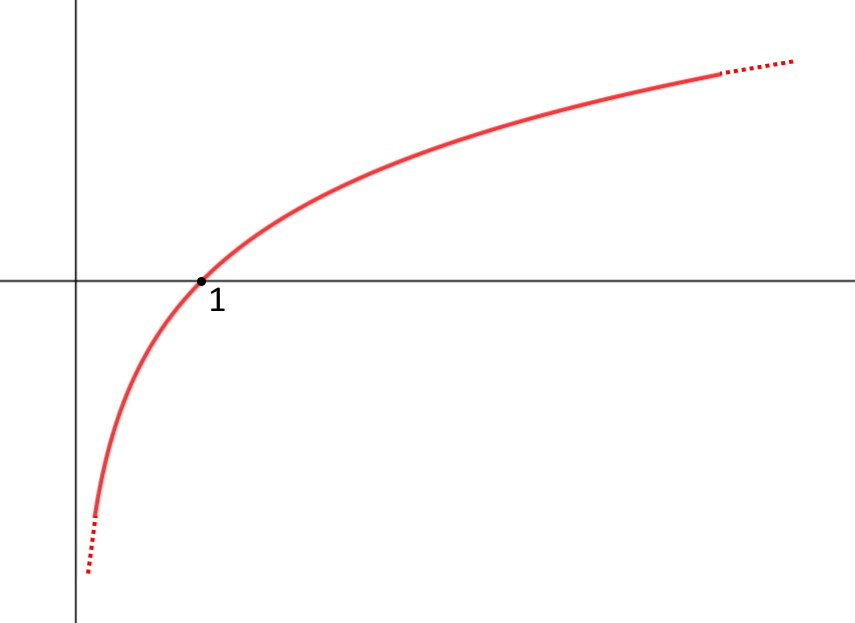
allora il logaritmo di una quantità leggermente più grande di 4 fa un numero poco più grandicello di 1, cioè:
\log_4 4 = 1 \implies \log_4 4^+ = 1^+
Quando non sapete certe cose, vedete grafico e andate per tentativi e logica! Non avrete problemi.
Ritorniamo al limite.
\frac{\log_2 4^+ +1}{3 \log_4 4^+ -3} =\frac{\log_2 4^+ +1}{3\cdotp 1^+ -3} = \frac{\log_2 4^+ +1}{3^+ -3} = \frac{\log_2 4^+ +1}{0^+} =+ \infin
In questo caso era fondamentale mettere il 3^+ perchè ci ha dato il segno dell’infinito. Invece il numeratore notiamo che è un numero positivo, quindi è ok. Non abbiamo nemmeno bisogno di calcolarlo perchè un numero positivo diviso zero fa + infinito. E’ chiaro che se forse veniva negativo il numeratore a quel punto dovevamo calcolarlo, perchè poi veniva -infinito!
In questo capitoletto abbiamo visto come risolvere esercizi sui limiti semplici. Adesso vediamo alcuni casi in cui il limite tende ad infinito.
Limite con x che tende a infinito
esercizi svolti
Esercizio 8. \lim\limits_{x\to - \infin } (x + \frac{5}{x} )
Il primo step come abbiamo fatto nel primo esercizio, è suddividere il limite in due limiti più semplici, grazie alla proprietà 2.
\lim\limits_{x\to - \infin } (x + \frac{5}{x} ) = \lim\limits_{x\to - \infin } x + \lim\limits_{x\to - \infin } \frac{5}{x} =
Il primo limite è semplice, non bisogna fare null’altro che sostituire il punto nella quale tende, quindi – infinito.
= - \infin + \lim\limits_{x\to - \infin } \frac{5}{x} =
Ricordate! Nel primo termine non c’è più il simbolo del limite, perchè abbiamo già effettuato il limite! Cioè abbiamo già sostituito il punto alla quale tende! Nel secondo termine non abbiamo sostituito nulla, quindi va tenuto!
Sostituiamo anche nel secondo termine il – infinito ed otteniamo:
= - \infin + \frac{5}{- \infin} =
Qualsiasi numero diviso infinito tende a zero, non è esattamente zero ma è molto vicino, è piccolissimo. Vediamo nella tabella il risultato, e ci accorgiamo che c’è un segno meno, quindi:
\frac{5}{- \infin} = 0^-
0^- significa un numero piccolissimo, che tende a zero, ma con un segno meno! In parole povere ed in maniera molto pratica potete immaginare questo numero come 0^- = -0,000000.....0001. Cioè un numero piccolissimo ma con un segno. Ritornando al limite, il risultato finale è:
= - \infin + 0^-
Ora abbiamo la somma di una quantità grandissima come meno infinito, e una quantità piccolissima: potete immaginare che se sommo un numero gigantesco con uno zero riottengo lo stesso numero gigantesco. Lo zero non aggiunge nulla nella somma. Il numero che prevale è meno infinito, quindi:
= - \infin + 0^- = - \infin
Esercizio 9. \lim\limits_{x\to - \infin } (-x^2 +x)
Anche in questo caso, la prima e furba cosa da fare è spezzare in due il limite.
\lim\limits_{x\to - \infin } (-x^2 +x) =\lim\limits_{x\to - \infin } -x^2 + \lim\limits_{x\to - \infin } x
Sostituiamo semplicemente il meno infinito, e vediamo cosa ne esce fuori.
\lim\limits_{x\to - \infin } -x^2 + \lim\limits_{x\to - \infin } x =-(- \infin )^2 + (-\infin ) =
Meno infinito al quadrato deve dare sicuramente un numero positivo. Il risultato non è \infin ^2, ma visto che con infinito si indica il “numero” più grande che ci sia, l’infinito rimane infinito. Cioè più grande di infinito non c’è nulla. Quindi qualsiasi operazione come 2 \cdotp \infin = \infin o \infin ^2 = \infin ecc.
Ritorniamo al limite. Abbiamo quindi:
-(- \infin )^2 + (-\infin ) =- (\infin) - \infin = -\infin - \infin = -\infin
Per ciò detto in precedenza non è due volte meno infinito, ma rimane sempre infinito e basta, poichè è una sorta di limite massimo sopra la quale non si può andare.
Esercizio 10. \lim\limits_{x\to + \infin } (2-x)\log x
Questo è leggermente diverso dagli altri, perchè abbiamo una funzione nuova: la funzione logaritmo. Quando avete il prodotto di funzioni diverse o comunque un qualche prodotto generale fra funzioni, non conviene spezzare il limite. Ma andiamo a sfruttare la proprietà 3.
\lim\limits_{x\to + \infin } (2-x)\log x =\lim\limits_{x\to + \infin } (2-x) \cdotp \lim\limits_{x\to + \infin } \log x =
=(2- \infin ) \log (+\infin )
Quanto fa il \log (+ \infin)? La risposta si trova vedendo un attimo il grafico della funzione stessa.
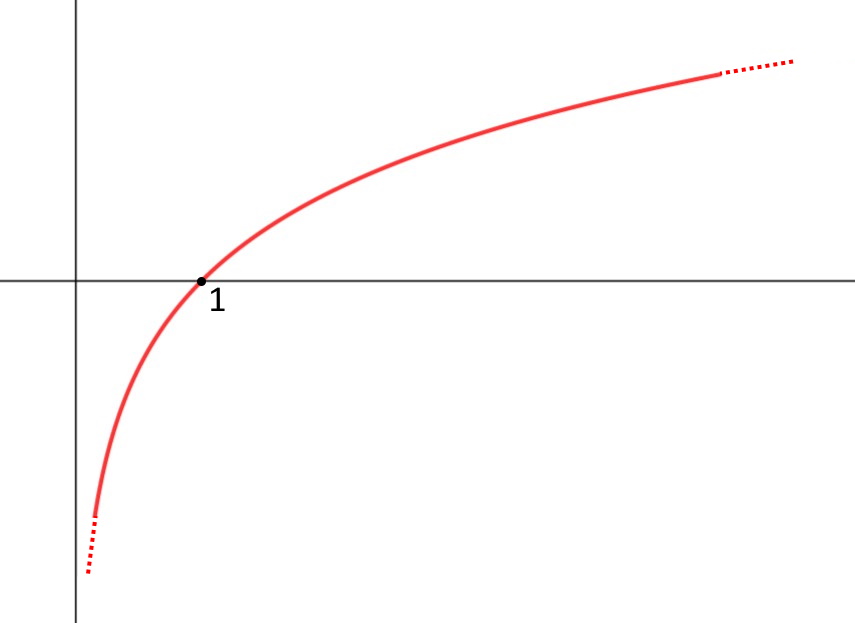
Come potete vedere se la coordinata x sull’ascisse va a + \infin , cioè va verso l’estrema destra, possiamo vedere che la funzione logaritmo tende ad andare sempre più sopra, cioè in corrispondenza di un punto sull’ordinata che va sempre più sopra. Cioè anche il logaritmo tende ad andare verso + \infin . Quindi \log (+ \infin) = + \infin
IMPORTANTE! Questo non vale solo per il logaritmo, per qualsiasi funzione vedete il grafico e capite subito! Senza fare conti!
Sostituiamo questo dato nel risultato finale e vediamo cosa esce:
(2- \infin ) \log (+\infin ) = (-\infin) \cdotp (+\infin) = -\infin
Chiaramente 2 meno infinito fa di nuovo meno infinito, perchè due non è confrontabile col meno infinito. (-\infin) \cdotp (+\infin) fa meno infinito, perchè abbiamo per la regola dei segni che: + per – fa -, e gli infiniti rimangono infinito! Una quantità infinita moltiplicata per una quantità infinita fa sempre una quantità infinita.
Aumentiamo un poco la difficoltà ora!
Esercizi sui limiti
difficoltà MEDIA
Esercizio 11. \lim\limits_{x\to 0^+} \frac{3^x \ln x }{2+x}
Il denominatore di questo limite non dà nessun problema: se andassimo a sostituire in (x+2) darebbe sempre 2; sul numeratore dobbiamo prestare leggermente più attenzione. Più che altro non sul 3^x ma sul logaritmo naturale. Dobbiamo capire quanto fa \ln 0^+, e per arrivarci vediamo sempre il grafico:
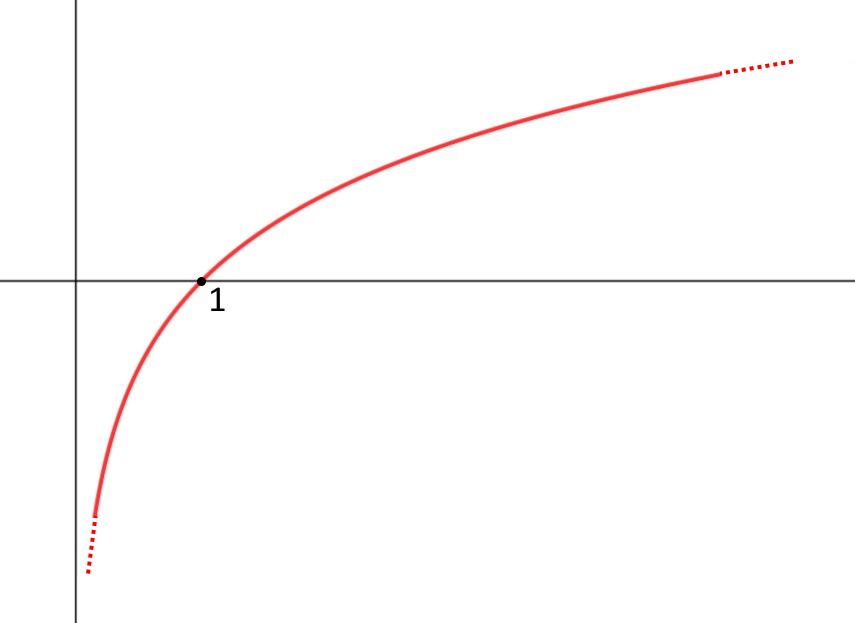
Si vede che per un numero poco più piccolo di zero il logaritmo tende a - \infin .
Quindi ritornando al limite:
\lim\limits_{x\to 0^+} \frac{3^x \ln x }{2+x} = \frac{3^0 \ln 0^+ }{2} =\frac{-\infin}{2}=-\infin
Esercizio 12. Quanto vale il \lim\limits_{x\to 0} \ln x ?
Rivediamo il grafico dell’esercizio precedente! Nell’esercizio precedente avevamo detto che nel limite in cui x tende a 0^+ la funzione logaritmo tendeva a meno infinito, ma ora non abbiamo che la x tende a 0^+ ma abbiamo che tende esattamente a x=0 e qui la funzione logaritmo non ci arriva mai! Nel punto dell’ascisse esattamente in x=0 il logaritmo non esiste in x=0! Cioè il logaritmo non ha nessun valore! Quindi:
\lim\limits_{x\to 0} \ln x = \nexists
Vedete sempre i grafici! E non sempre si ha un valore del limite che esiste!
Esercizio 13. \lim\limits_{x\to + \infin } (-x3^x \ln x )^2
Allora, procediamo per ordine: su -x basta sostituire e non c’è problema; 3^x segue lo stesso grafico più o meno dell’esponenziale che abbiamo visto prima, tende quindi a infinito per x che tende a infinito:
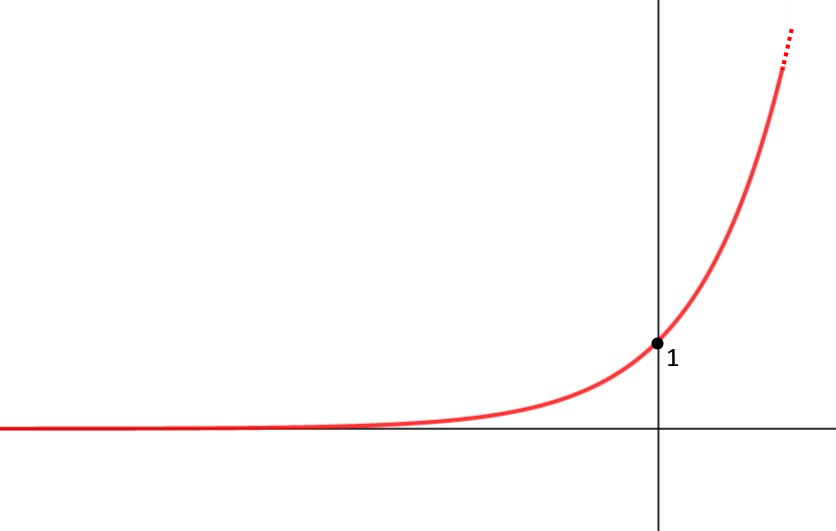
Il logaritmo lo abbiamo visto tante volte e tende anch’esso a + infinito. Ora che abbiamo tutto, andiamo a sostituire:
\lim\limits_{x\to + \infin } (-x3^x \ln x )^2 =(- \infin 3^\infin \ln \infin )^2 = (-\infin \cdotp \infin \cdotp \infin )^2 = (- \infin )^2 = + \infin
dove ricordiamo come sempre che l’infinito moltiplicato per infinito dà sempre infinito. I segni seguono la regola dei segni: + per – fa -, – per – fa + ecc.
Esercizio 14. \lim\limits_{x\to 1} \frac{2x -1 }{\log x -3} \frac{ 1}{(1-x)^2}
Qui sostituiamo semplicemente e stiamo attenti ai segni.
\lim\limits_{x\to 1} \frac{2x -1 }{\log x -3} \frac{ 1}{(1-x)^2} = \frac{2 -1 }{\log 1 -3} \frac{ 1}{(1-1)^2}
Il \log 1 = 0 e potete farlo anche a calcolatrice per vederlo. La quantità al secondo denominatore (1-1)^2 =0 fa chiaramente zero. Segue che:
\frac{2 -1 }{\log 1 -3} \frac{ 1}{(1-1)^2} = \frac{1 }{0 -3} \frac{ 1}{0} = - \frac{1}{3} \frac{1}{0}
La quantità \frac{1}{0} = \infin fa infinito, come potete vedere dalla tabella. Infinito moltiplicato per -\frac{1}{3} fa meno infinito: cioè un infinito moltiplicato per un numero negativo fa meno infinito. Il risultato quindi è:
- \frac{1}{3} \frac{1}{0} = - \infin
Continuiamo con gli esercizi svolti sui limiti!
Esercizio 15. \lim\limits_{x\to 1^-} ( \frac{2^x}{\ln x } + \frac{1}{x-1} )
Separiamo il limite in due pezzi più semplici ed esaminiamone uno alla volta.
\lim\limits_{x\to 1^-} ( \frac{2^x}{\ln x } + \frac{1}{x-1} ) = \lim\limits_{x\to 1^-} \frac{2^x}{\ln x }+ \lim\limits_{x\to 1^-} \frac{1}{x-1}
Analizziamo il primo pezzo. Al numeratore 2^{1^+} = 2 fa più o meno 2 e non ci dà problemi. Ricordatevi che per essere precisi 2^{1^+} = 2,0000....00001 ma non serve tutta questa precisione, quindi scriviamo solamente 2 e basta.
E’ importante essere precisi quando c’è di mezzo lo zero! Perchè fra un 0^- =-0,00...001 e uno 0^+ = +0,00..001 c’è una differenza enorme: uno è negativo e l’altro è positivo!
Invece 2^{1^+} = +2,000..0001 mentre 2^{1^-} = 1,999...999 e fanno entrambi +2.
Fatta questa parentesi andiamo avanti: ora dobbiamo considerare il \ln x con x che tende a 1^- e per far ciò vediamo il grafico.
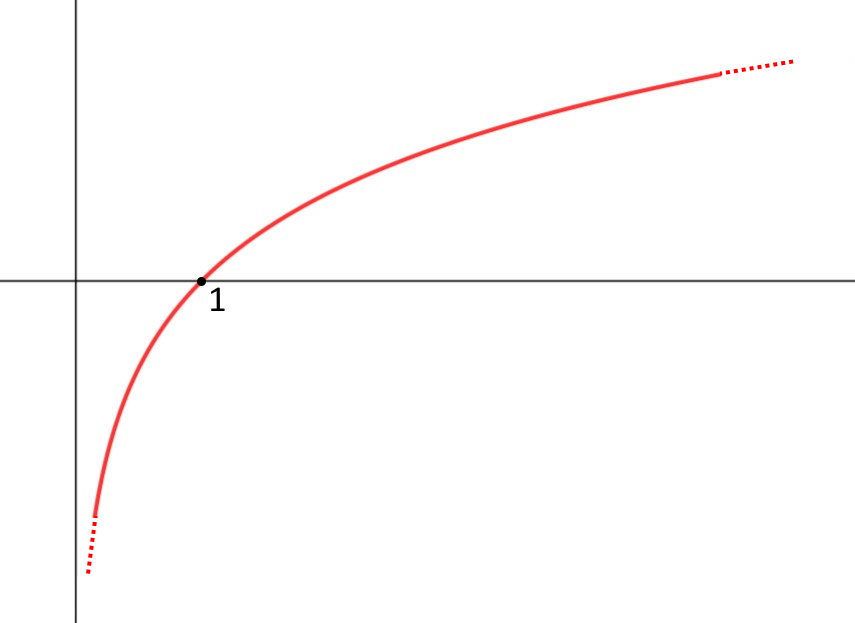
Il logaritmo in 1 fa zero: \ln 1 = 0 come potete vedere dal grafico, mentre in un punto un poco prima di x=1 ossia un poco più a sinistra, cioè in x=1^- il logaritmo inizia a diventare negativo. Ma si avvicina comunque molto a zero. Allora deduciamo che \ln 1^- = 0^-
Allora abbiamo: \lim\limits_{x\to 1^-} \frac{2^x}{\ln x } = \frac{2}{0^- } =- \infin
Passiamo ora ad analizzare il secondo limite, come vedete è molto a ragionamento i limiti!
\lim\limits_{x\to 1^-} \frac{1}{x-1}
Al denominatore dobbiamo capire quanto fa x-1 con x che tende a 1^-. Il numero 1^- significa un 1 un poco più piccoletto di 1, ossia per intenderci 0,9999999…
Quindi 1^- -1 = 0,999... - 1 = -0,000000....01 = 0^-
E allora:
\lim\limits_{x\to 1^-} \frac{1}{x-1}=\frac{1}{1^- -1}= \frac{1}{0^-}=- \infin
Sommando i due risultati dei limiti otteniamo la soluzione:
=- \infin - \infin = - \infin
Esercizio 16. \lim\limits_{x\to + \infin} (\log_{\frac{1}{3}} x - xe^x )
Questo è un esercizio assolutamente diverso dagli altri. Ora vedremo perchè. Iniziamo a suddividere in due il limite.
\lim\limits_{x\to + \infin} (\log_{\frac{1}{3}} x - xe^x ) =\lim\limits_{x\to + \infin} \log_{\frac{1}{3}} x - \lim\limits_{x\to + \infin} xe^x
Sul primo c’è da stare attenti. La base del nostro logaritmo qui è \frac{1}{3}. Il grafico del logaritmo con una base che appartiene all’intervallo ]0,1[ ha un grafico diverso rispetto a quelli che abbiamo visto fin ora. Il grafico è:
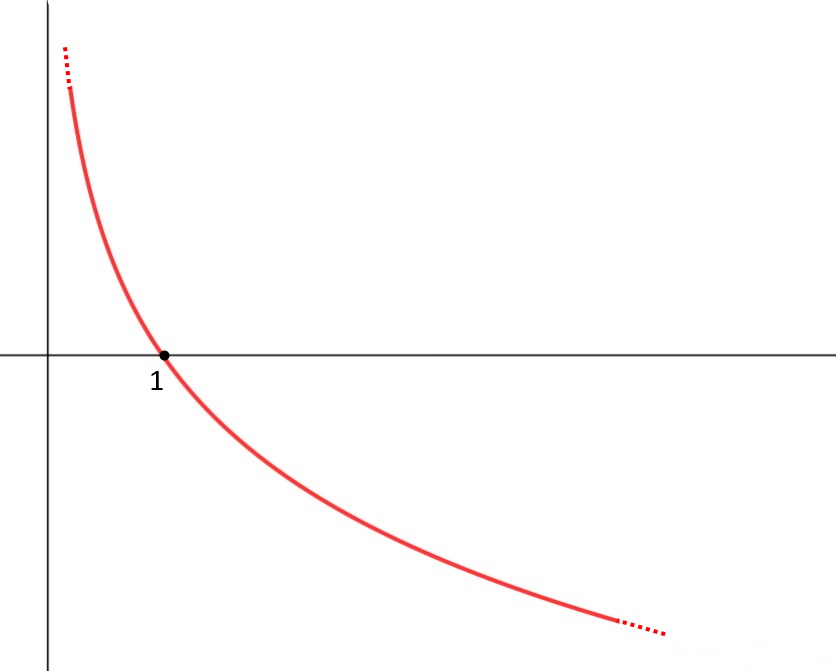
E quindi abbiamo il risultato opposto! Per x che tende ad infinito il logaritmo con questa base tende a meno infinito!
\lim\limits_{x\to + \infin} \log_{\frac{1}{3}} x = - \infin
Passiamo ora al secondo termine. Questo è più semplice. Sostituiamo semplicemente:
\lim\limits_{x\to + \infin} xe^x = \infin e^\infin = \infin
Ed otteniamo, ricordandoci del segno meno prima di quest’ultimo limite:
=-\infin - \infin = - \infin
Esercizio 17. \lim\limits_{x\to 0^+} (\frac{\sin x }{\ln x} + \frac{1}{\cos x } )
Cosa facciamo per prima cosa? Ovviamente, essendo una somma, la spezziamo!
\lim\limits_{x\to 0^+} (\frac{\sin x }{\ln x} + \frac{1}{\cos x } ) =\lim\limits_{x\to 0^+} \frac{\sin x }{\ln x} + \lim\limits_{x\to 0^+} \frac{1}{\cos x }
Studiamo il primo pezzo \lim\limits_{x\to 0^+} \frac{\sin x }{\ln x}.
Abbiamo già visto sia il seno che il logaritmo naturale. Per x che tende ad un valore poco più grande di zero, il seno tende anch’esso ad un valore poco più grande di zero, essendo crescente. Il logaritmo naturale come visto nell’esercizio 11. per x che tende a 0^+ tende a - \infin , quindi:
\lim\limits_{x\to 0^+} \frac{\sin x }{\ln x} =\frac{\sin 0^+ }{\ln 0^+} = \frac{ 0^+ }{- \infin } =0
Fa zero perchè zero diviso qualsiasi numero fa sempre zero. Non ci interessa del segno perchè zero rimane zero.
Passiamo al secondo limite \lim\limits_{x\to 0^+} \frac{1}{\cos x }.
Questo è semplice. Vedendo il grafico del coseno di seguito disegnato, possiamo notare che per x che tende ad un valore poco più grande di zero il coseno è all’incirca 1.
\lim\limits_{x\to 0^+} \frac{1}{\cos x } =\frac{1}{\cos 0^+ } = \frac{1}{1} = 1
Quindi sommando anche il risultato di prima abbiamo che la soluzione è:
=0 +1 = 1
Continuiamo con gli esercizi svolti sui limiti!
Esercizio 18. \lim\limits_{x\to 0} \frac{\arctg x +2x}{\cos x}
Qui abbiamo la funzione arcotangente che non avevamo ancora visto. Il discorso è sempre lo stesso: vedere il grafico!
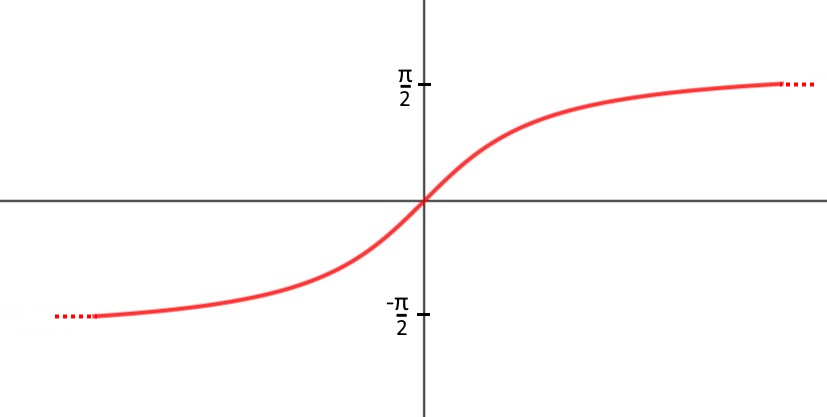
Come si può notare per x che tende a x=0 l’arcotangente tende anch’essa a 0. Il limite è così immediato.
\lim\limits_{x\to 0} \frac{\arctg x +2x}{\cos x} = \frac{\arctg 0 +0}{\cos 0} = \frac{0}{1}=0
Esercizio 19. \lim\limits_{x\to 1^-} \frac{\arcsin x}{x-1}
Per quanto riguarda la funzione arcoseno, vediamo il grafico come si comporta.
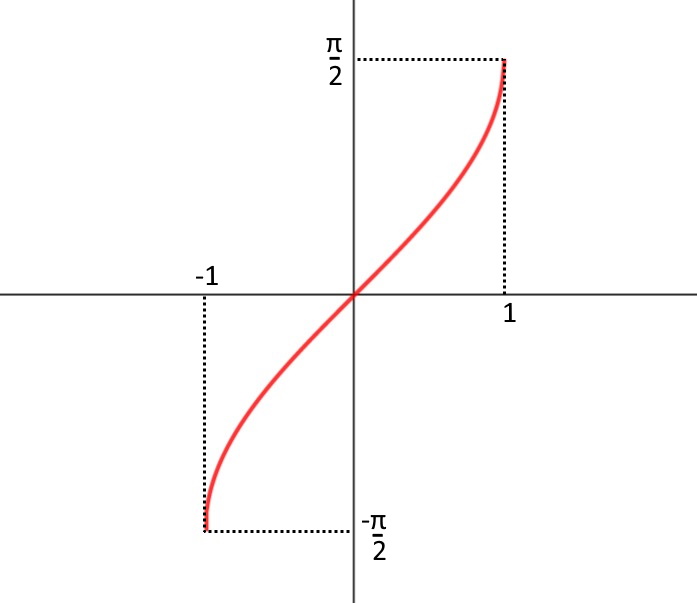
Notiamo immediatamente che per x\to 1^- la funzione assume il valore di \frac{\pi}{2}.
Per quanto riguarda l’analisi del denominatore l’abbiamo già fatta prima, ma la ripetiamo per chi non l’avesse vista.
In termini pratici 1 meno è un pochetto più piccolo di 1: 1^- = 0,999....99, quindi:
1^- - 1 = 0,999....99 - 1 = -0,00...001 = 0^-
Allora segue che nel limite:
\lim\limits_{x\to 1^-} \frac{\arcsin x}{x-1} =\frac{\arcsin 1^-}{1^- -1} =\frac{ \frac{\pi}{2} }{0^-}= - \infin
Esercizio 20. \lim\limits_{x\to \frac{\pi}{2}^+} e^{\frac{1}{\cos x }}
La funzione coseno nel limite in cui x\to \frac{\pi}{2}^+, ossia poco dopo \frac{\pi}{2}, inizia a diventare negativa con un valore vicino allo zero: 0^-.
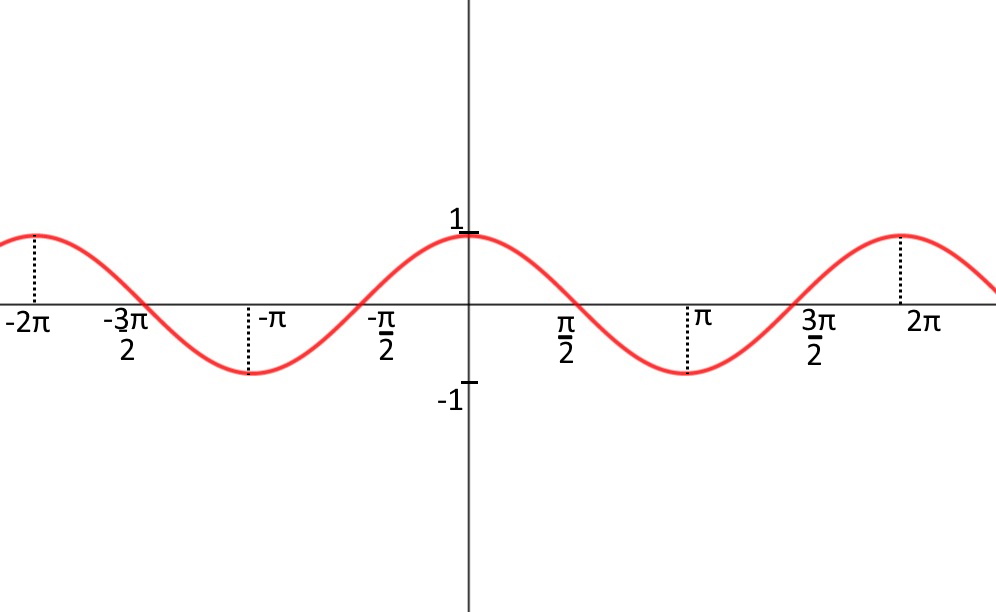
Sostituiamo nel limite ed otteniamo:
\lim\limits_{x\to \frac{\pi}{2}^+} e^{\frac{1}{\cos x }} = e^{\frac{1}{\cos \frac{\pi}{2}^+}} = e^{\frac{1}{0^-}}
\frac{1}{0^-}=- \infin come ben sappiamo. Quindi abbiamo:
e^{- \infin} =0 perchè la funzione esponenziale a meno infinito tende a zero.
Esercizi limiti
DIFFICILI
Esercizio 21. \lim\limits_{x\to + \infin} (x+ \sin x )
Suddividiamo in due i limiti:
\lim\limits_{x\to + \infin} (x+ \sin x ) = \lim\limits_{x\to + \infin} x +\lim\limits_{x\to + \infin} \sin x
Sul primo limite non ci sono dubbi! Per x che tende a infinito la funzione x tende a infinito:
\lim\limits_{x\to + \infin} x =+ \infin
Guardate il grafico del seno. Per x che tende a infinito, a quale valore tende il seno che oscilla sempre?
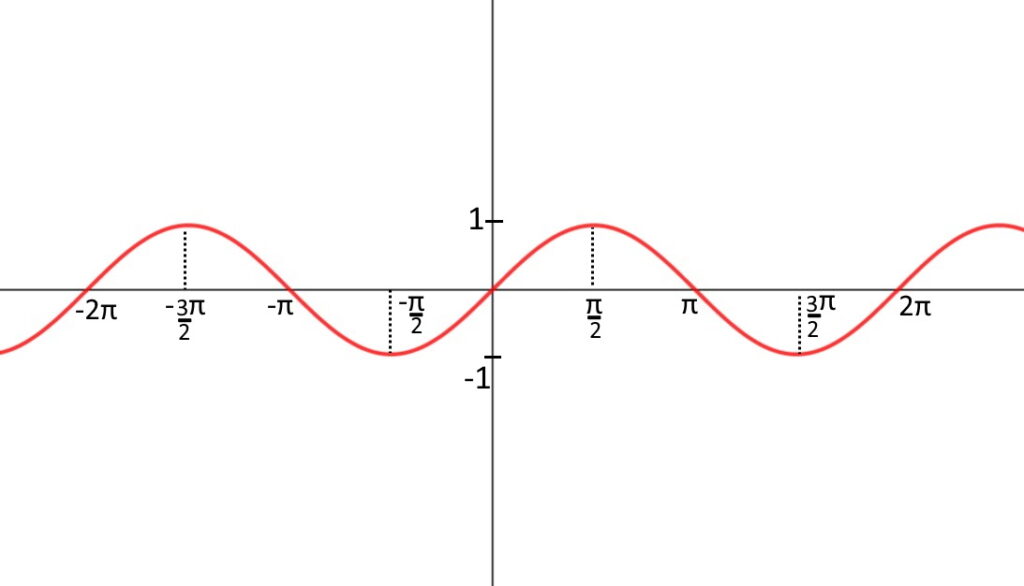
E qui è un problema, perchè non possiamo sapere a cosa tende di preciso il seno. La funzione seno continua ad oscillare e non tende a nessun valore preciso! Però possiamo notare una cosa: il seno oscilla fra -1 e +1, e continua ad oscillare sempre fra -1 e +1.
Quindi anche per x che tende a infinito il:
\lim\limits_{x\to + \infin} \sin x =h dove h è in [-1,+1].
E vabene così, perchè il risultato finale sarà:
\lim\limits_{x\to + \infin} x +\lim\limits_{x\to + \infin} \sin x =\infin + h = \infin
Infinito più un qualsiasi valore in [-1,+1] fa sempre infinito.
Esercizio 22. \lim\limits_{x\to - \infin} \frac{\ln (e^{2x} + 1)}{\ln (1-x)}
Iniziamo a sostituire il limite della x, e poi ragioniamoci su.
\lim\limits_{x\to - \infin} \frac{\ln (e^{2x} + 1)}{\ln (1-x)} =\frac{\ln (e^{-2 \infin} + 1)}{\ln (1-(- \infin))}
Ricordiamo che l’infinito rimane infinito e non segue nessuna regola di calcolo (apparte le forme indeterminate riguardo la frazione di infiniti ma poi la vedremo negli esercizi svolti sulle forme indeterminate).
\implies \frac{\ln (e^{- \infin} + 1)}{\ln (1 + \infin)} = \frac{\ln (e^{- \infin} + 1)}{\ln ( \infin)}
La funzione esponenziale decrescente e^{- \infin} tende a zero, visto il suo grafico. Mettiamoci lo zero quindi al suo posto (per non sbagliare mai si va passaggio alla volta e con calma!):
= \frac{\ln (0+ 1)}{\ln ( \infin)} =\frac{\ln ( 1)}{\ln ( \infin)}
Il logaritmo di qualsiasi base di 1 è sempre zero. Mentre visto il grafico del logaritmo, per x che tende a infinito, il logaritmo tende a infinito, quindi abbiamo:
=\frac{0}{ \infin)}
Qualsiasi numero diviso per infinito è zero (tranne se è infinito anch’esso), e lo zero non rappresenta un’eccezione! Viceversa: lo zero diviso per qualsiasi cosa (tranne con un altro zero) fa sempre zero. Quindi arriviamo al risultato:
\frac{0}{ \infin)} =0
Continuiamo con gli esercizi svolti sui limiti!
Esercizio 23. \lim\limits_{x\to 1^+} ( \frac{1}{\sqrt{x-1}})^{x-2}
Con il limite per x\to 1^+ l’esponente tende alla -1. Per quanto riguarda il valore x-1 all’interno della radice invece è un discorso che già abbiamo fatto. In maniera pratica per vedere a cosa tende vi mostro il procedimento: CONSIGLIO! Ciò che vi faccio vedere adesso e che abbiamo già visto è perfetto per capire un qualcosa a cosa tende, ma non lo scrivete esplicitamente nella verifica in classe: ad alcuni professori non piace, chissà!
x\to 1^+ di x-1 è 1^+ -1=1,00...001 - 1 = 0,00..001 = 0^+
Sostituiamo il tutto:
\lim\limits_{x\to 1^+} ( \frac{1}{\sqrt{x-1}})^{x-2} = ( \frac{1}{\sqrt{1^+ -1}})^{1^+ -2} =( \frac{1}{\sqrt{0^+}})^{-1}
=\sqrt{0^+} =0 semplicemente mettendo il denominatore al numeratore, visto l’esponente alla -1.
Esercizio 24. \lim\limits_{x\to - \infin} \frac{2^x}{(x^2 -x ) \ln (1-x)}
Partiamo dal numeratore che è immediato. Un numero elevato a qualcosa (se tale numero è >1 ) si comporta come un’esponenziale. E sappiamo che tale nel limite in cui x tende alla meno infinito, tende a zero!
\lim\limits_{x\to - \infin} 2^x =2^{- \infin }=0
Beh e qualsiasi numero diviso 0 fa sempre 0! Quindi potremmo dire che il risultato sarà zero senza analizzare il denominatore? Purtroppo c’è una forma indeterminata che è 0 diviso 0. Quindi dobbiamo evitare che fuoriesca un risultato del genere, bisogna controllare, altrimenti bisogna fare dei passaggi spiegati in forme indeterminate.
\lim\limits_{x\to - \infin} (x^2 -x ) \ln (1-x) = (\infin + \infin ) \ln ( \infin) = \infin
Quindi il risultato finale è zero! Dove abbiamo considerato che il limite del logaritmo per x che tende ad infinito, vedendo nel grafico già visto decine di volte in questa pagina, tende a infinito.
Esercizio 25. \lim\limits_{x\to 2^+} (\frac{x-2}{e^{x-2}})^{\frac{1}{x-2}}
Nel limite abbiamo per ben tre volte il termine x-2, quindi analizziamolo da parte: applichiamo gli stessi ragionamenti degli altri esercizi. Ormai avete imparato come si fanno questi limiti base! Ma vi assicuro che le forme indeterminate e i limiti notevoli sono di una difficoltà ben superiore. Ma studiando su questo sito capirete in qualche giorno tutto!
\lim\limits_{x\to 2^+} x-2 = 2^+ - 2 = 2,00...001 - 2 = 0,00..01 = 0^+
Mettiamo tale risultato nel limite intero.
\lim\limits_{x\to 2^+} (\frac{x-2}{e^{x-2}})^{\frac{1}{x-2}} = (\frac{2^+-2}{e^{2^+-2}})^{\frac{1}{2^+-2}}=(\frac{0^+}{e^{0^+}})^{\frac{1}{0^+}}
Abbiamo 2 funzioni diverse: un esponenziale e^{0^+} ed una frazione \frac{1}{0^+}.
L’esponenziale tende ad 1 ovviamente: e elevato alla zero tende ad 1. La frazione ha un numero positivo 1 diviso per zero positivo che fa + infinito. Qui mettere il 0^+ piuttosto che il solo 0 è fondamentale per capire esattamente il segno.
(\frac{0^+}{e^{0^+}})^{\frac{1}{0^+}} =(\frac{0^+}{1})^{+ \infin} =(0^+)^{+ \infin}=0^+
Dove potevamo anche mettere lo 0 solo. Zero elevato alla infinito fa zero e non rientra nelle forme indeterminate, anche se lo può sembrare.
Esercizio 26. \lim\limits_{x\to -1} \frac{x + \sin (3^{x+1} -1 ) }{\arcsin (x+1)^2}
Partiamo dal denominatore che è più semplice ed immediato e l’arcoseno l’abbiamo già visto. Il limite di \lim\limits_{x\to -1} (x+1)^2 = 0 e l’arcseno di zero è zero: \arcsin 0 = 0. Ora direte: ok, qualsiasi cosa divisa per zero fa infinito è chiaro! Beh no, perchè se anche il numeratore è zero allora è una forma indeterminata ed è tutt’altro discorso. Poi supponendo che sia un numero diverso da zero, è importante calcolarlo perchè dobbiamo capire il segno dell’infinito!
\lim\limits_{x\to -1} x + \sin (3^{x+1} -1 ) = -1 + \sin (3^0 -1 ) = -1 + \sin (1-1)=-1 +\sin 0 =-1 +0=-1
Grazie a ciò possiamo dare un segno preciso all’infinito. Abbiamo:
\frac{-1}{0}=- \infin
Esercizio 27. \lim\limits_{x\to 0} \frac{\sin (2^x -1) + \log_2 (x+2)}{\cos (x+ \pi )}
Al denominatore abbiamo \lim\limits_{x\to 0} \cos (x+ \pi ) = \cos (\pi ) = -1.
Al numeratore abbiamo \lim\limits_{x\to 0} \sin (2^x -1) = \sin (2^0 -1)= \sin 0 = 0
Ed abbiamo anche \lim\limits_{x\to 0} \log_2 (x+2) = \log_2 (0+2) = \log_2 2= 1 perchè ricordiamo che un logaritmo con base e argomento uguali fa sempre 1.
Il risultato finale è quindi -1.
Come potete vedere la tattica vincente è studiare, in questi casi, il limite analizzandoli per parti: una funzione alla volta. Questa tattica, come vedremo, si rivelerà fallimentare per i limiti più complicati che vedremo negli esercizi svolti delle forme indeterminate e limiti notevoli. Non perdiamoci in chiacchiere e concludiamo gli esercizi risolti con l’ultimo capitoletto di 3 esercizi!
Continuiamo con gli esercizi svolti sui limiti!
Esercizi svolti limiti col Teorema del CONFRONTO
Esercizio 28. Calcolare il limite \lim\limits_{x\to + \infin} \frac{\sin x}{x} col teorema del confronto.
La funzione seno che non ammette limite, è compresa fra -1 e +1.
-1 \le \sin x \le +1
Nel nostro limite abbiamo \frac{\sin x}{x}
e allora dividiamo -1 \le \sin x \le +1 per x!
-\frac{1}{x} \le \frac{\sin x }{x} \le +\frac{1}{x}
Abbiamo praticamente messo a confronto la funzione del nostro limite con altre due funzioni. Il teorema del confronto non ha una formula particolare da imparare a memoria, semplicemente con alcuni ragionamenti si cerca di mettere a confronto la nostra funzione con altre più semplici e di cui conosciamo il limite.
Per x\to + \infin sia - \frac{1}{x} che + \frac{1}{x} tendono a zero.
Quindi nel limite x\to + \infin abbiamo che 0 \le \frac{\sin x }{x} \le 0
e l’unica soluzione che possiamo avere è che il termine in mezzo (cioè la funzione del nostro esercizio) sia anch’esso zero!
Esercizio 29. Calcolare il limite \lim\limits_{x\to + \infin} \frac{\cos x}{x} col teorema del confronto.
E’ molto simile all’esercizio precedente! Prima di vedere la soluzione, provate a farlo voi! E’ molto simile, dai!
La funzione coseno che non ammette limite perchè oscilla sempre, è compresa fra -1 e +1.
-1 \le \cos x \le +1
Nel nostro esercizio si ha: \frac{\cos x}{x}
Come fatto prima, dividiamo tutto per x nel confronto per ottenere la funzione del nostro esercizio.
-\frac{1}{x} \le \frac{\cos x }{x} \le +\frac{1}{x}
Per x\to + \infin sia - \frac{1}{x} che + \frac{1}{x} tendono a zero.
Quindi nel limite x\to + \infin abbiamo che 0 \le \frac{\cos x }{x} \le 0
e l’unica soluzione che possiamo avere è che il termine in mezzo (cioè la funzione del nostro esercizio) sia anch’esso zero!
Esercizio 30. Calcolare il limite \lim\limits_{x\to + \infin} \frac{2x}{3+ \sin x} col teorema del confronto.
Come prima partiamo dalla funzione di cui non conosciamo il limite: il seno.
Come detto prima abbiamo che:
-1 \le \sin x \le +1
Qui però abbiamo 3 + \sin x , quindi addizioniamo +3 al tutto.
-1 +3 \le 3 +\sin x \le +1+3
2 \le 3 +\sin x \le 4
Nel nostro caso questa quantità è al denominatore, quindi facciamo il reciproco di tutto, ricordandoci che vanno invertiti i segni delle disequazioni:
\frac{1}{4} \le \frac{1}{3 +\sin x } \le \frac{1}{2}
Questo perchè se ho 4>2 e faccio il reciproco, il simbolo è invertito: \frac{1}{4} < \frac{1}{2} perchè sarebbe 0,25 < 0,5.
Ritornando all’esercizio, nel confronto moltiplichiamo per 2x il tutto.
\frac{2x}{4} \le \frac{2x}{3 +\sin x } \le \frac{2x}{2}
Per x\to + \infin gli estremi tendono a infinito:
+ \infin \le \frac{2x}{3 +\sin x } \le + \infin
Essendo la nostra funzione compresa, l’unica soluzione accettabile è che anch’essa sarà infinito!
Per approfondimenti sul teorema del confronto vedere:
https://it.wikipedia.org/wiki/Teorema_del_confronto#:~:text=Il%20teorema%20del%20confronto%20%C3%A8,pi%C3%B9%22%20intorno%20a%20quello%20dato.
Come risolvere i limiti

E l’ultimo consiglio riguarda il teorema del confronto, da considerare quando non sapete come risolvere il limite.
Gli esercizi svolti sui limiti non si fermano qui! Proseguite con altri esercizi svolti sui limiti sulle forme indeterminate e sui limiti notevoli !
Trovate altri esercizi di matematica qui ed altro ancora!
indeterminate
esercizi