Esercizi svolti limiti NOTEVOLI: 25 ESERCIZI !
Esercizi svolti limiti NOTEVOLI: 25 ESERCIZI ! Verifica in classe o esame in arrivo? Quale sito migliore per studiare, eccovi ben 20 esercizi svolti sul calcolo dei limiti notevoli che sono sicuramente l’argomento più importante per l’esame finale! Prima di passare a quest’ultimo step, è importante che sappiate le basi del calcolo dei limiti e delle forme indeterminate. Cliccateci sopra e avrete altri esercizi svolti che in una giornata riuscirete a capire! Di seguito troverete l’indice che vi porta ai vari capitoli di questa lezione sugli esercizi. Partiremo da un formulario che potete scrivere su un foglietto per ricordarvelo e poi passeremo al mettere in pratica ogni singolo limite notevole. Alla fine ci saranno dei consigli da seguire! Iniziamo subito!
Indice
- Tabella dei limiti notevoli
- Limite notevole: \lim\limits_{x \to 0} \frac{\sin x}{x} = 1
- Limite notevole: \lim\limits_{x \to 0} \frac{1- \cos x}{x} = 0
- Limite notevole: \lim\limits_{x \to 0} \frac{1- \cos x}{x^2} = \frac{1}{2}
- Limite notevole: \lim\limits_{x \to \pm \infin} (1+\frac{1}{x} )^x = e
- Limite notevole: \lim\limits_{x \to 0} \frac{\ln (1+x) }{x} = 1
- Limite notevole: \lim\limits_{x \to 0} \frac{e^x -1}{x} = 1
- Limite notevole: \lim\limits_{x \to 0} \frac{ (1+x)^k -1 }{x} = k
- Consigli generali per la verifica in classe.
Iniziamo subito con gli esercizi svolti sui limiti notevoli!
Limiti notevoli tabella
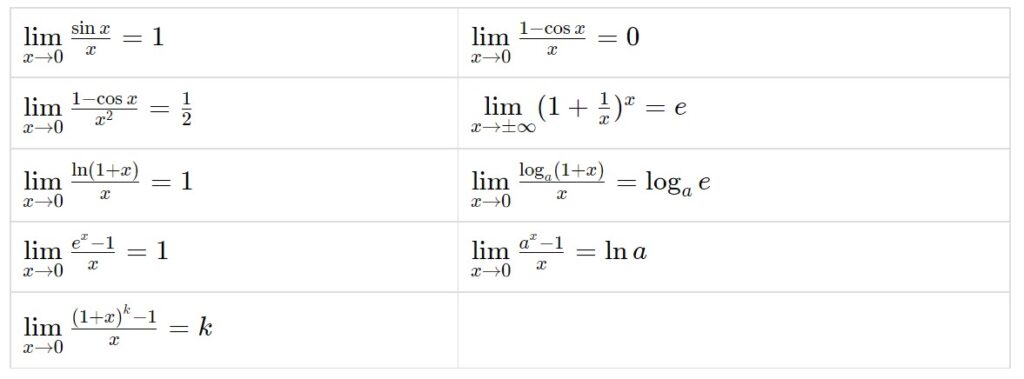
Iniziamo subito con gli esercizi svolti sui limiti notevoli!
Esercizi limite notevole:
\lim\limits_{x \to 0} \frac{\sin x}{x} = 1
Esercizio 1. \lim\limits_{x \to 0 } \frac{\sin 5x }{x}
Il limite notevole a cui ci dobbiamo rifare è chiaramente:
\lim\limits_{x \to 0} \frac{\sin x}{x} = 1
Quando abbiamo un limite che è leggermente diverso da uno notevole, quello che possiamo fare è la seguente cosa: moltiplichiamo e dividiamo per 5.
\lim\limits_{x \to 0 } \frac{\sin 5x }{5x} \cdotp 5
A questo punto pongo 5x=y, quindi y=\frac{x}{5}.
Sostituiamo nel limite:
\lim\limits_{\frac{y}{5} \to 0 } \frac{\sin y }{y} \cdotp 5
Quello che possiamo notare è che se x tende a 0 anche y tende a 0 (visto 5x=y), quindi o scriviamo y/5 o scriviamo y è la stessa cosa perchè entrambi tendono a 0:
\lim\limits_{y \to 0 } \frac{\sin y }{y} \cdotp 5
Ed abbiamo ottenuto il limite notevole che conosciamo! Anzi che avere scritto la x abbiamo scritto la y che è la stessa identica cosa! O una variabile o l’altra sempre vale:
\lim\limits_{y \to 0} \frac{\sin y}{y} = 1
L’importante è che siamo uguali le quantità al posto della x nel limite notevole. Cioè per esempio non vale:
\lim\limits_{y \to 0} \frac{\sin y}{2y} = 1 !!!!
Mentre vale:
\lim\limits_{z \to 0} \frac{\sin z}{z} = 1 !!!!
Torniamo al nostro esercizio.
\lim\limits_{y \to 0 } \frac{\sin y }{y} \cdotp 5 = 1 \cdotp 5 = 5
Esercizio 2. \lim\limits_{x \to 0 } \frac{\sin kx }{x}
Stesso procedimento di prima! Questo tipo di ragionamento ricorre sempre quindi è importante capirlo!
Moltiplichiamo e dividiamo per k:
\lim\limits_{x \to 0 } \frac{\sin kx }{kx} \cdotp k
Poniamo kx=y, e notiamo che se x tende a 0 anche y tende a 0, perchè k \cdotp 0 = 0
\lim\limits_{y \to 0 } \frac{\sin y }{y} \cdotp k
Sfruttiamo ora il limite notevole:
\lim\limits_{y \to 0} \frac{\sin y}{y} = 1
E quindi otteniamo come risultato:
\lim\limits_{y \to 0 } \frac{\sin y }{y} \cdotp k = 1 \cdotp k = k
Esercizio 3. \lim\limits_{x \to 0 } \frac{\sin^2 2x }{x^2}
Notiamo immediatamente che possiamo scrivere:
\lim\limits_{x \to 0 } \frac{\sin^2 2x }{x^2} = \lim\limits_{x \to 0 } \frac{\sin 2x }{x} \cdotp \frac{\sin 2x }{x}
E come prima moltiplichiamo e dividiamo per 2 per ben 2 volte, perchè abbiamo due limiti notevoli che compaiono.
= \lim\limits_{x \to 0 } \frac{\sin 2x }{2x} 2 \cdotp \frac{\sin 2x }{2x} 2 = \lim\limits_{x \to 0 } \frac{\sin 2x }{2x} \cdotp \frac{\sin 2x }{2x} \cdotp 4
Come fatto in precedenza, poniamo 2x=y. Notiamo inoltre che se x tende a 0 anche y tende a 0, quindi otteniamo:
\lim\limits_{y \to 0 } \frac{\sin y }{y} \cdotp \frac{\sin y }{y} \cdotp 4 =
=\lim\limits_{y \to 0 } \frac{\sin y }{y} \cdotp \lim\limits_{y \to 0 } \frac{\sin y }{y} \cdotp 4 = 1 \cdotp 1 \cdotp 4 = 4
Esercizio 4. \lim\limits_{x \to 0 } \frac{\cos^2 x -1 }{2x}
Il numeratore ci fa venire immediatamente in mente la formula madre della trigonometria:
\sin^2 x + \cos^2 x = 1
Da cui segue:
\sin^2 x + \cos^2 x - 1 = - \sin^2 x
Sostituiamo nel nostro limite il risultato ottenuto e scriviamo il limite come un limite notevole che conosciamo moltiplicato per tutto il resto.
\lim\limits_{x \to 0 } \frac{- \sin^2 x }{2x} = \frac{\sin x }{x} \cdotp (-\frac{\sin x }{2} )
=\lim\limits_{x \to 0 }\frac{\sin x }{x} \cdotp \lim\limits_{x \to 0 } (-\frac{\sin x }{2} )
Il primo è un limite notevole di cui conosciamo il risultato, sul secondo sostituiamo semplicemente perchè non ci dà nessun problema!
=1 \cdotp (-\frac{\sin 0 }{2} ) = 0
Continuiamo con gli esercizi svolti limiti notevoli!
Esercizio 5. \lim\limits_{x \to 0 } \frac{\sin x +2x \cos x }{x \cos x + 2 \sin x}
Il nostro obiettivo è quello di far comparire dei limiti notevoli che conosciamo. In questo caso notiamo che: mettendo in evidenza la x sia al numeratore che al denominatore allora esce fuori il limite notevole che conosciamo e la x si semplifica.
\lim\limits_{x \to 0 } \frac{x(\frac{\sin x}{x} +2 \cos x )}{x( \cos x + 2 \frac{\sin x}{x} ) }= \lim\limits_{x \to 0 } \frac{\frac{\sin x}{x} +2 \cos x }{ \cos x + 2 \frac{\sin x}{x} }
A questo punto risolviamo il limite, ricordandoci che:
\lim\limits_{x \to 0} \frac{\sin x}{x} = 1
=\frac{1 +2 \cos 0 }{ \cos 0 + 2 } = \frac{1+2}{1+2}=1
Limiti notevoli per x che tende ad infinito
Vediamo un esempio in cui il limite tende all’infinito, mentre noi vorremmo che tendesse a zero…
Esercizio 6. \lim\limits_{x \to \infin } x \sin \frac{1}{x}
Per ovviare al problema, un po’ come fatto nel primo esercizio, poniamo:
y=\frac{1}{x} \implies x=\frac{1}{y}
Sostituendo otteniamo:
\lim\limits_{x \to \infin } \frac{1}{y} \sin y
A questo punto bisogna chiaramente anche sostituire la x che tende ad infinito. Notiamo che se x tende ad infinito, y tende a zero, vedendo y=\frac{1}{x} perchè y=\frac{1}{\infin} =0
E quindi otteniamo sotto forma di altra variabile il limite notevole!
\lim\limits_{y \to 0 } \frac{1}{y} \sin y = 1
Continuiamo con gli esercizi svolti limiti notevoli!
Esercizi limiti notevoli:
\lim\limits_{x \to 0} \frac{1- \cos x}{x} = 0
Esercizio 7. \lim\limits_{x \to 0 } \frac{1- \sqrt{ \cos x } }{x}
Questo ci ricorda il limite notevole:
\lim\limits_{x \to 0} \frac{1- \cos x}{x} = 0
Effettivamente notiamo che, come fatto in precedenti lezioni, se moltiplichiamo e dividiamo per lo stesso numeratore ma cambiato di segno allora otteniamo questo limite notevole, e possiamo risolvere il limite!
\lim\limits_{x \to 0 } \frac{1- \sqrt{ \cos x } }{x} \frac{1+ \sqrt{ \cos x }}{1+ \sqrt{ \cos x }}
E poi sfruttiamo la relazione algebrica:
(a-b)(a+b)=a^2 - b^2
Quindi il nostro limite diventa:
= \lim\limits_{x \to 0 } \frac{1- \cos x }{x(1+ \sqrt{ \cos x })}
A questo punto è comparso il limite notevole che volevamo, ed inoltre il limite adesso dà un risultato accettabile!
= 0 \cdotp \frac{1}{1+ \sqrt{ \cos 0 }}= 0
Continuiamo con gli esercizi svolti limiti notevoli!
Esercizio 8. \lim\limits_{x \to 0^- } e^{\frac{\sin x}{1- \cos x} }
Notiamo che all’esponente vi è:
- al denominatore c’è metà del limite notevole \lim\limits_{x \to 0} \frac{1- \cos x}{x} = 0 ;
- al numeratore c’è metà del limite notevole \lim\limits_{x \to 0} \frac{\sin x}{x} = 1.
A tutti e due gli manca una x, quindi moltiplichiamo e dividiamo per x l’esponente della e.
\lim\limits_{x \to 0^- } e^{\frac{x \sin x}{x(1- \cos x}) }
Abbiamo ora sia il limite notevole \lim\limits_{x \to 0} \frac{\sin x}{x} = 1
sia il limite notevole seguente, però al contrario \lim\limits_{x \to 0} \frac{1- \cos x}{x} = 0
Possiamo risolvere il limite! Scriviamo separatamente i due limiti notevoli per comodità:
= \lim\limits_{x \to 0^- } e^{\frac{ \sin x}{x} \frac{x}{1- \cos x} } = \lim\limits_{x \to 0^- } e^{\frac{ \sin x}{x} (\frac{1- \cos x}{x})^{-1} }
Sostituiamo i risultati dei limiti notevoli e concludiamo l’esercizio:
=e^{1 \cdotp (0^-)^{-1} } = e^{1 \cdotp \frac{1}{0^-} } = e^{-\infin} = 0^+
Esercizio 9. \lim\limits_{x \to 0 } \frac{x^2 \cos x }{2-2 \cos x}
Mettiamo in evidenza il 2 innanzitutto.
\lim\limits_{x \to 0 } \frac{x^2 \cos x }{2(1- \cos x )}
In realtà come prima, abbiamo il reciproco del limite notevole. Quindi lo scriviamo in questo modo equivalente:
\lim\limits_{x \to 0 } \frac{\cos x }{2} (\frac{1- \cos x}{x^2 })^{-1}
E risolviamo il limite!
= \frac{\cos 0 }{2} (\frac{1}{2 })^{-1} = \frac{1}{2} \cdotp 2 = 1
Continuiamo con gli esercizi limiti notevoli!
Esercizi svolti con i limiti notevoli:
\lim\limits_{x \to 0} \frac{1- \cos x}{x^2} = \frac{1}{2}
Esercizio 10. \lim\limits_{x \to 0^+ } \frac{\sqrt{1 - \cos^2 x} }{x}
Quella radice ci dà fastidio, però a levarla sarebbe non facile. Portare la x all’interno della radice è molto più semplice invece. Notiamo che:
x = \sqrt{ x^2 }
Quindi scriviamolo così all’interno del limite, e poi portiamo tutto sotto una comune radice, per una proprietà delle radici.
\lim\limits_{x \to 0^+ } \frac{\sqrt{1 - \cos^2 x} }{\sqrt{ x^2 }} =\lim\limits_{x \to 0^+ } \sqrt{\frac{1 - \cos^2 x}{x^2} }
Sfruttiamo la differenza dei quadrati, per far sì di levare il quadrato al coseno, che è il nostro obiettivo!
\lim\limits_{x \to 0^+ } \sqrt{\frac{1 - \cos^2 x}{x^2} } = \lim\limits_{x \to 0^+ } \sqrt{\frac{(1 - \cos x)(1+ \cos x)}{x^2} }
Da qui risolviamo il limite, poiché abbiamo finalmente quello della formula di questo paragrafo. Notate inoltre che nel limite notevole o x tende a 0 o tende a 0^+ in questi casi non fa differenza.
=\sqrt{\frac{1}{2} (1 + \cos 0) } = \sqrt{\frac{1}{2} (1 + 1) } = 1
Esercizio 11. \lim\limits_{x \to 0 } \frac{2x^2 }{1- \cos x}
Questo ci ricorda sicuramente il limite notevole seguente, però all’incontrario:
\lim\limits_{x \to 0} \frac{1- \cos x}{x^2} = \frac{1}{2}
Notiamo che abbiamo il reciproco del limite notevole, ciò non è un problema. Quello che possiamo fare sicuramente è una semplice riscrittura in un questa forma equivalente:
\lim\limits_{x \to 0 } \frac{2x^2 }{1- \cos x} = \lim\limits_{x \to 0 } (\frac{1- \cos x }{2x^2})^{-1}
E scriviamo la costante moltiplicativa separata.
=\lim\limits_{x \to 0 } (\frac{1}{2} \cdotp \frac{1- \cos x }{x^2})^{-1}
A questo punto abbiamo fatto comparire il limite notevole, e quindi possiamo risolvere il limite.
= (\frac{1}{2} \cdotp \frac{1}{2} )^{-1} = (\frac{1}{4} )^{-1} = 4
Continuiamo con gli esercizi svolti con i limiti notevoli!
Limiti notevoli esercizi svolti:
\lim\limits_{x \to \pm \infin} (1+\frac{1}{x} )^x = e
Esercizio 12. \lim\limits_{x \to - \infin } (\frac{x-7}{x} )^x
Sicuramente la forma è chiara e ci vogliamo ricondurre al limite notevole seguente:
\lim\limits_{x \to \pm \infin} (1+\frac{1}{x} )^x = e
Spezziamo la frazione, scrivendo due termini separati.
\lim\limits_{x \to - \infin } (\frac{x}{x}-\frac{7}{x} )^x = \lim\limits_{x \to - \infin } (1-\frac{7}{x} )^x
Ciò che vogliamo è un qualcosa del tipo (1+\frac{1}{y}) all’interno della parentesi.
Effettuiamo una sostituzione e poniamo quindi:
-\frac{7}{x} =+ \frac{1}{y}
Dove facciamo il reciproco di tutta l’equazione per ottenere la x in funzione della y, cioè capovolgiamo tutto in parole povere.
-\frac{x}{7} =y \implies x=-7y
Nel nostro limite abbiamo che x \to - \infin, notando che x=-7y, allora se x tende a -infinito allora y tende a +infinito. Sostituiamo il tutto nel nostro limite dell’esercizio adesso!
\lim\limits_{y \to + \infin } (1+\frac{1}{y} )^{-7y}
Adesso dobbiamo un attimo cambiare l’esponente. Sfruttiamo la proprietà delle potenze seguente:
a^{bc} = (a^b)^c
Nel nostro caso:
\lim\limits_{y \to + \infin } [(1+\frac{1}{y} )^y ]^{-7}
Quello all’interno è il limite notevole, risolviamo l’esercizio.
=e^{-7}
Esercizio 13. \lim\limits_{x \to + \infin } (\frac{x^2 +1}{x^2} )^{2x^2}
Anche in questo caso, come accade molto spesso in questi tipi di limiti, spezziamo la frazione:
\lim\limits_{x \to + \infin } (\frac{x^2}{x^2} + \frac{1}{x^2})^{2x^2}=\lim\limits_{x \to + \infin } (1 + \frac{1}{x^2})^{2x^2}
Poniamo:
\frac{1}{x^2}=\frac{1}{y} \implies x^2 =y \implies x=\sqrt{y}
Abbiamo che se x tende a +infinito, cioè il caso nostro, anche la y tende a +infinito. Quindi:
\lim\limits_{y \to + \infin } (1 + \frac{1}{y})^{2y}
Ed utilizziamo la stessa regola delle potenze citata prima.
= \lim\limits_{y \to + \infin } [(1 + \frac{1}{y})^y ]^2
Quello all’interno è il nostro caro limite notevole.
= e^2
Esercizio 14. \lim\limits_{x \to -\infin } (\frac{x+2}{x+1})^x
Scriviamo il numeratore x+2 come x+1+1. In tale modo possiamo spezzare la frazione e semplificare.
= \lim\limits_{x \to -\infin } (\frac{x+1+1}{x+1})^x = \lim\limits_{x \to -\infin } (\frac{x+1}{x+1}+\frac{1}{x+1} )^x
=\lim\limits_{x \to -\infin } (1+\frac{1}{x+1} )^x
Continuiamo sempre per sostituzione. Poniamo:
\frac{1}{x+1} = \frac{1}{y} \implies x+1=y \implies x=y-1
Nel nostro limite abbiamo che x tende a -infinito, se x tende a – infinito la y tende a -infinito, visto che x=y-1, quindi:
=\lim\limits_{y \to -\infin } (1+\frac{1}{y} )^{y-1}
Sfruttiamo adesso la proprietà delle potenze secondo la quale:
a^{b+c}=a^b a^c
Nel nostro caso allora:
=\lim\limits_{y \to -\infin } (1+\frac{1}{y} )^y (1+\frac{1}{y} )^{-1}
Il primo è il limite notevole solito, il secondo non ci dà problemi.
=e (1+\frac{1}{-\infin} )^{-1} = e(1+0)^{-1}=e
Continuiamo con gli limiti notevoli esercizi svolti!
Limiti notevoli con ln:
\lim\limits_{x \to 0} \frac{\ln (1+x) }{x} = 1
Esercizio 15. \lim\limits_{x \to 0 } \frac{\ln (x+5) -\ln 5 }{ x}
Adesso vediamo come trattare esercizi dei limiti notevoli con ln, ossia il logaritmo naturale, cioè un logaritmo con base e, che è un numero che vale 2,7…
Mettiamo qui in evidenza all’interno del logaritmo il 5.
=\lim\limits_{x \to 0 } \frac{\ln 5(\frac{x}{5}+1) -\ln 5 }{ x}
ed utilizziamo la proprietà dei logaritmi seguente:
=\ln ab = \ln a + \ln b
Quindi nel nostro caso:
=\lim\limits_{x \to 0 } \frac{\ln 5 + \ln(\frac{x}{5}+1) -\ln 5 }{ x} =\lim\limits_{x \to 0 } \frac{ \ln(\frac{x}{5}+1) }{ x}
Ed ora poniamo \frac{x}{5}=y \implies x= 5y
Se x tende a 0 anche y tende a 0. Sostituiamo:
=\lim\limits_{y \to 0 } \frac{ \ln(y+1) }{ 5y} =\lim\limits_{y \to 0 } \frac{1}{5} \frac{ \ln(y+1) }{ y} =\frac{1}{5}
Esercizio 16. \lim\limits_{x \to +\infin } x[\ln (x+1) - \ln x ]
Ciò che ci dà fastidio è quella x al numeratore e la y che tende ad infinito. Poniamo allora subito:
x=\frac{1}{y}
In tal modo se x tende ad infinito la y tende a 0. Inoltre abbiamo ora la y al denominatore e pian piano sta figurando il limite notevole.
\lim\limits_{y \to 0 } \frac{\ln (\frac{1}{y}+1) - \ln \frac{1}{y} }{y}
E facciamo il minimo comune multiplo all’interno del primo logaritmo:
\lim\limits_{y \to 0 } \frac{\ln (\frac{1+y}{y}) - \ln \frac{1}{y} }{y}
In tal modo possiamo utilizzare sia per il primo logaritmo che per il secondo la proprietà:
\ln \frac{a}{b} = \ln a - \ln b
Quindi per il nostro limite:
\lim\limits_{y \to 0 } \frac{\ln (1+y) - \ln y - \ln 1 + \ln y }{y} =\lim\limits_{y \to 0 } \frac{\ln (1+y) }{y}
perchè ricordiamo che il ln 1=0, ora abbiamo risolto l’esercizio con risultato:
=1
Esercizio 17. \lim\limits_{x \to +\infin } x[\ln (x^2 +4 ) -2\ln x ]
Questa non è facile sicuramente. Dobbiamo sfruttare fin da subito la seguente proprietà del logaritmo:
b \ln a = \ln a^b
Quindi il secondo logaritmo diventa \ln x^2
E poi utilizziamo la proprietà secondo la quale:
\ln a - \ln b = \ln \frac{a}{b}
E quindi nel nostro limite abbiamo che:
\lim\limits_{x \to +\infin } x[\ln (x^2 +4 ) -\ln x^2 ]=\lim\limits_{x \to +\infin } x[\ln (\frac{x^2 +4}{x^2} ) ]
=\lim\limits_{x \to +\infin } x \ln (1 + \frac{4}{x^2} )
A questo punto poniamo:
\frac{4}{x^2}=y \implies x=\sqrt{\frac{4}{y} } = \frac{2}{\sqrt{y} }
Se x tende a infinito la y tende a 0, il limite diventa:
\lim\limits_{y \to 0 } 2 \frac{\ln (1 + y )}{\sqrt{y}}
Abbiamo il limite che tende a 0, abbiamo il logaritmo messo bene, il denominatore dobbiamo cambiarlo. Moltiplichiamo e dividiamo allora per \sqrt{y}!
=\lim\limits_{y \to 0 } 2 \frac{\ln (1 + y )}{\sqrt{y}} \frac{\sqrt{y}}{\sqrt{y}} =\lim\limits_{y \to 0 } 2 \frac{\ln (1 + y )}{y} sqrt{y}
Abbiamo quindi il limite notevole che compare adesso!! Risolviamo il limite:
=2 \cdotp 1 \cdotp \sqrt{0} = 0
Questi erano dei limiti notevoli con ln, ossia con la presenza di logaritmi naturali.
Continuiamo con altri esercizi svolti limiti notevoli!
Limiti notevoli con e:
\lim\limits_{x \to 0} \frac{e^x -1}{x} = 1
Esercizio 18. \lim\limits_{x \to 0 } \frac{e^{-2x} -1 }{x}
Adesso vediamo dei limiti notevoli con e, che è un numero per chi non lo sapesse, ed in particolare vale 2,7…ma negli esercizi dei limiti notevoli con e lo rimaniamo così com’è.
Qui è abbastanza immediato, come fatto già tante volte e come spesso si fa nei limiti notevoli, poniamo:
-2x=y \implies x=-\frac{y}{2}
Se x tende a 0, anche y tende a 0. Sostituiamo il tutto nel limite:
\lim\limits_{y \to 0 } \frac{e^y -1 }{-\frac{y}{2}} =\lim\limits_{y \to 0 } -2 \frac{e^y -1 }{y}
Abbiamo una costante moltiplicata per un limite notevole, gioco fatto!
=-2 \cdotp 1 = -2
Esercizio 19. \lim\limits_{x \to 0 } \frac{e^{x+2} - e^2}{x}
L’esercizio qui è abbastanza immediato, nel senso che basta scrivere esplicitamente il primo esponenziale usando la proprietà:
a^{b+c} = a^b a^c
E quindi nel nostro caso abbiamo:
\lim\limits_{x \to 0 } \frac{e^x e^2 - e^2}{x}
E poi mettiamo in evidenza e^2.
\lim\limits_{x \to 0 } \frac{e^2 (e^x - 1)}{x} =
\lim\limits_{x \to 0 } e^2 \cdotp \frac{e^x - 1}{x} =e^2 \cdotp 1 = e^2
Esercizio 20. \lim\limits_{x \to 0 } \frac{e^x - e^{-x} }{8x}
Aggiungiamo e sottraiamo al numeratore 1 e poi spezziamo il limite in due limiti separati in modo da far comparire il limite notevole.
\lim\limits_{x \to 0 } \frac{e^x - e^{-x} +1-1}{8x}=\lim\limits_{x \to 0 } \frac{e^x -1 }{8x} + \lim\limits_{x \to 0 } -\frac{e^{-x} -1 }{8x}
Il primo limite è immediato, e fa:
=\lim\limits_{x \to 0 } \frac{1}{8} \frac{e^x -1 }{x} = \frac{1}{8}
Per il secondo limite invece, poniamo -x=y. Per x che tende a 0, anche y tende a 0. Sostituiamo nel secondo limite chiaramente solo, perchè il primo l’abbiamo già risolto.
= \lim\limits_{y \to 0 } -\frac{e^y -1 }{-8y} = \lim\limits_{y \to 0 } \frac{e^y -1 }{8y}=
= \lim\limits_{y \to 0 } \frac{1}{8} \frac{e^y -1 }{y}= \frac{1}{8}
Uniamo adesso le due soluzioni insieme ed otteniamo:
=\frac{1}{8}\frac{1}{8} +\frac{1}{8} = \frac{2}{8} =\frac{1}{4}
I limiti notevoli con e sono finiti.
Continuiamo con altri esercizi svolti limiti notevoli!
Esercizi sui limiti notevoli:
\lim\limits_{x \to 0} \frac{ (1+x)^k -1 }{x} = k
Esercizio 21. \lim\limits_{x \to 0 } \frac{\sqrt{1+x} -1 }{2x}
Innanzitutto scriviamo la radice sotto forma di esponente esplicito e poi mettiamo il 2 al denominatore da parte.
\lim\limits_{x \to 0 } \frac{1}{2} \frac{(1+x)^{\frac{1}{2}} -1 }{x}
Considerando che abbiamo il limite notevole \lim\limits_{x \to 0} \frac{ (1+x)^k -1 }{x} = k
dove k=\frac{1}{2} nel nostro caso allora abbiamo come risultato:
=\frac{1}{2} \cdotp \frac{1}{2}
Esercizio 22. \lim\limits_{x \to 0 } \frac{(1+2x)^5 -1 }{5x}
Quello che vogliamo è un numeratore identico al limite notevole, quindi procediamo come fatto già per tanti altri esercizi, per sostituzione:
2x=y \implies x=c
E chiaramente se x tende a 0 anche y tende a 0. Sostituiamo il tutto nel limite del nostro esercizio:
\lim\limits_{y \to 0 } \frac{(1+y)^5 -1 }{5 \frac{y}{2}} =\lim\limits_{y \to 0 } \frac{2}{5} \frac{(1+y)^5 -1 }{y}
=\frac{2}{5} 5 = 2
Gli esercizi sui limiti notevoli sono finiti.
Abbiamo concluso finalmente questa parte di esercizi!
Come risolvere i limiti notevoli

Se volete ancora esercitarvi di più, magari cliccate sulle forme indeterminate o sulle basi del calcolo dei limiti!
Continuate a studiare sul nostro sito dove c’è tanta roba! Supportateci!
Se volete approfondire i limiti notevoli:
https://it.wikipedia.org/wiki/Limite_notevole
Limiti notevoli esercizi svolti
indeterminate
esercizi
esercizi
svolti