Funzione inversa: definizione, come calcolarla, grafici ed esempi
Funzione inversa: definizione, come calcolarla, grafici ed esempi. In questa ricca pagina vedremo tutto sulle funzioni inverse, partendo dalla teoria fino a degli esercizi svolti di calcolo. Inoltre mostreremo come ricavare l’inversa del seno, del logaritmo ecc. Troverete tutto! Iniziamo subito!
Indice
- Funzione inversa: definizione
- Grafico della funzione inversa
- Come calcolare una funzione inversa, esempi
- Continuità della funzione inversa
Senza perdere altro tempo vediamo subito la definizione!
Funzione inversa: definizione

Dom (f) e Im(f) rappresentano rispettivamente il dominio della funzione, ed la sua immagine. Quindi in breve quello che stiamo facendo è invertire dominio con la sua immagine! Attenzione che molti libri e siti confondono immagine con il codominio, quindi può risultare difficile capirne la differenza.
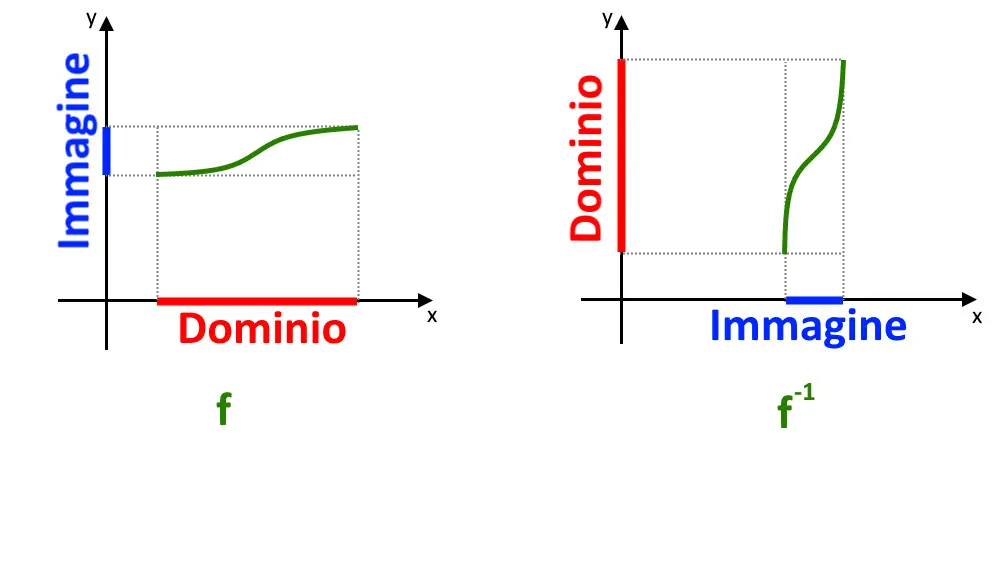
Adesso spieghiamo tutto in maniera più dettagliata. All’inizio abbiamo una funzione biettiva f: dom(f) \to Im(f) , ossia una funzione che prende un valore del dominio dom(f) e ne associa uno solo dell’immagine della funzione Im(f). Quello che facciamo è invertire i due insiemi. Cioè creiamo una nuova funzione (che si chiama l’inversa) che adesso prende un valore dell’immagine della funzione Im(f) e ne associa uno solo del dominio dom(f) (f^{-1}:Im(f) \to dom(f) ). Cioè stiamo facendo il percorso inverso, il procedimento invertito!
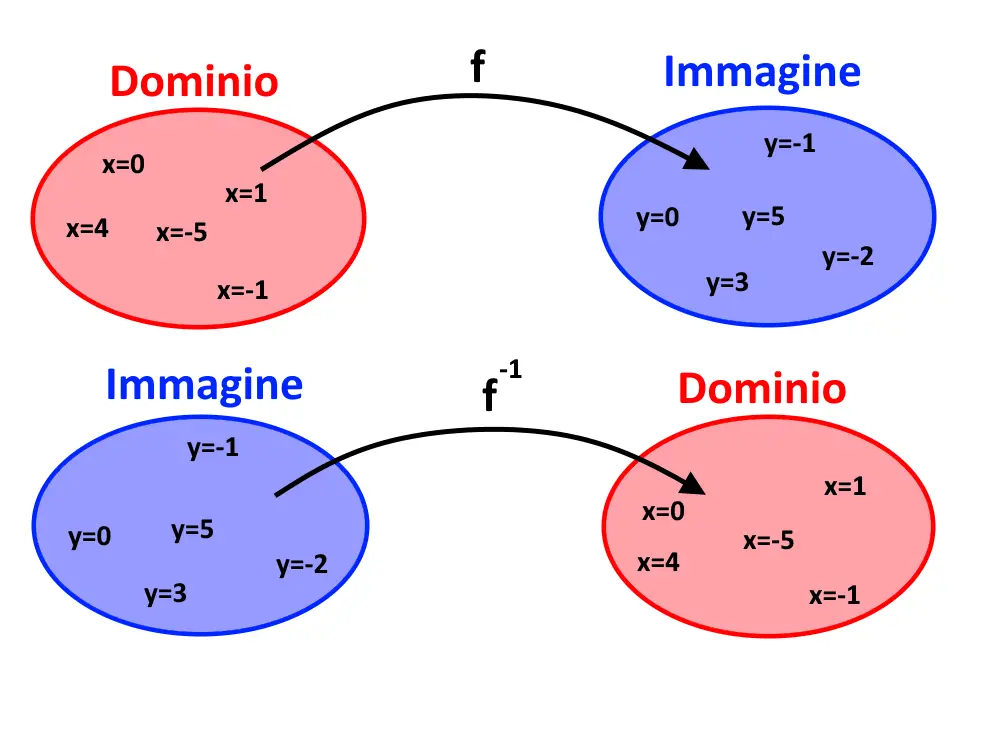
Una volta che si fa questo procedimento, se prima avevamo una y=f(x), adesso col procedimento inverso si ha una x=f^{-1} (y) . Come vedete dallo schema di sopra degli insiemi, adesso si parte dall’insieme Im(f) (immagine di f) cui ha valori su y. Di conseguenza anche gli assi risultano invertiti.
E visto che ciò a noi non piace, andiamo a rinominare gli assi, richiamando quello orizzontale x e quello verticale y!
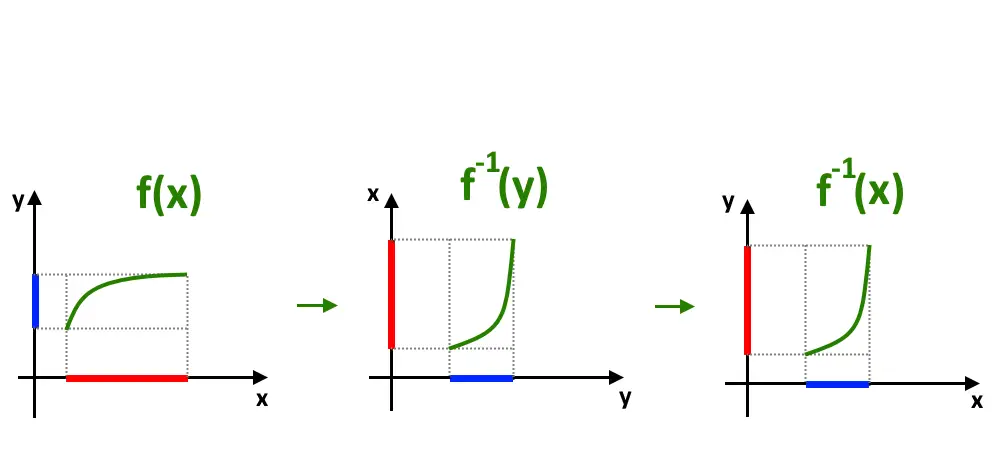
Ed in questo modo riabbiamo gli assi scritti normali, ma con gli insiemi invertiti.
L’asse x e dominio non è la stessa cosa? No, l’asse x è una retta con verso e dei numeri sopra. Il dominio invece è una parte di questa retta. In alcuni casi può anche essere tutta la retta, ma dipende dalla funzione.
Perché c’è bisogno che sia biettiva? Biettiva significa che associa ad ogni x un solo valore di y e viceversa. Ad esempio la seguente funzione non è biettiva, perché associa ad ogni y più valori di x. Di conseguenza se andiamo ad invertire dominio e immagine e grafichiamo la f^{-1} , quella non è una funzione. Questo perché ricordiamo che si dice funzione se ad ogni x viene associata una sola y, e ciò non accade più in questo caso.
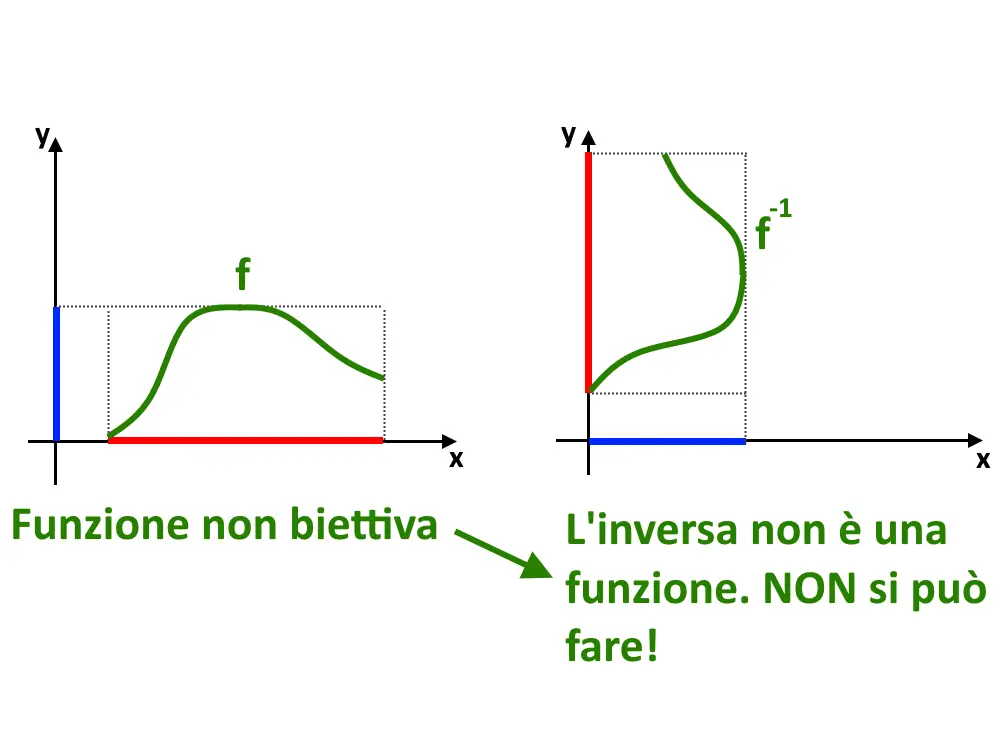
Va bene tutto ma: se ho una certa funzione, come faccio a trovare il grafico di quella inversa?
Grafico di una funzione inversa
Consideriamo una funzione biettiva (nella sezione prima abbiamo capito l’importanza di essere biettiva) f: dom(f) \to Im(f) , ad esempio la seguente.
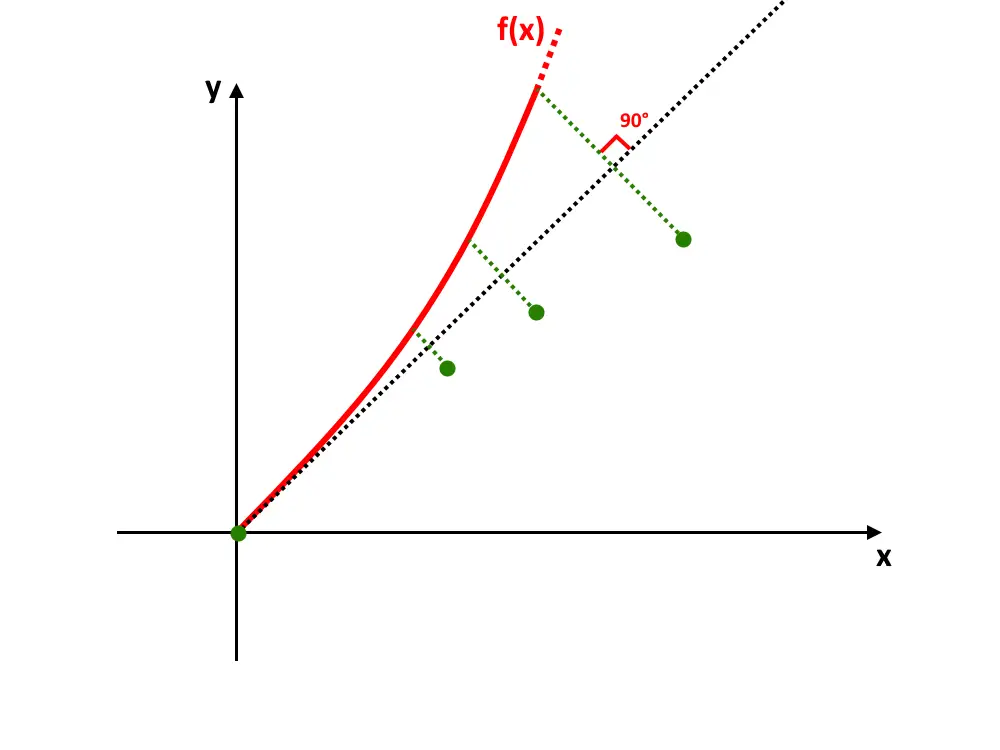
Come faccio a trovare il grafico della sua inversa? Per trovare il grafico dell’inversa, bisogna disegnare la bisettrice del primo e terzo quadrante (ossia una retta tratteggiata che divide l’angolo del primo quadrante in due parti uguali, cioè una retta a 45° di pendenza).
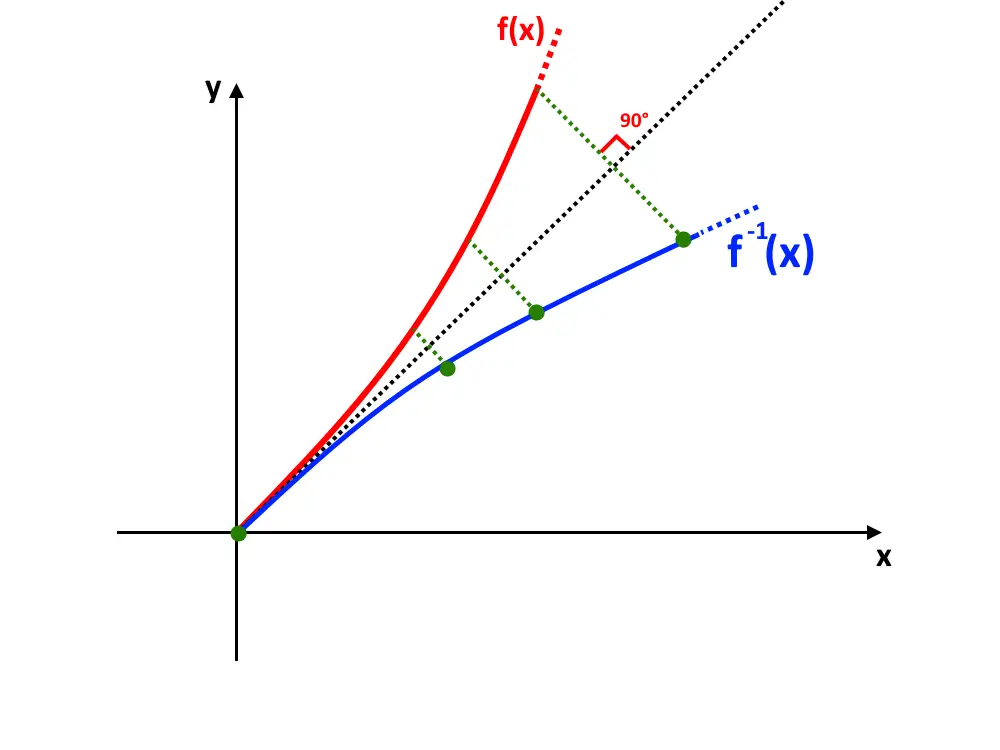
Dopo di che, segniamo punti della funzione simmetrici a tale bisettrice. Cioè prendiamo diversi punti della funzione e andiamo a disegnare un segmento che taglia la bisettrice in maniera perpendicolare. Inoltre tale segmento, per essere simmetrico chiaramente, deve essere di lunghezza uguale da una parte e dall’altra della bisettrice.
Unendo i punti, troviamo il grafico della funzione inversa.
Se volete altri esempi di grafici e anche calcoli espliciti, nella sezione successiva ne trovate!
Calcolo della funzione inversa, esempi
In questa sezione vedremo anche come effettuare il calcolo esplicito per trovare la forma della funzione inversa, oltre che il grafico.
Il procedimento generale che seguiremo è il seguente:
- Abbiamo una y=f(x)
- Troviamo la x=^{-1}(y)
- Invertiamo i nomi: x \to y, \; y \to x
- Ed abbiamo la funzione inversa y=^{-1}(x)
Esempio 1. Troviamo la funzione inversa di y= 2x-1 .
Come vedete abbiamo una y=f(x). Per trovare la x=^{-1}(y) , in pratica vogliamo la x a sinistra. Quindi portiamo il 2x a sinistra e la y a destra. Ricordate che, come una equazione quando si porta da una parte all’altra si cambia di segno:
-2x= -y-1
Cambiamo tutto di segno (vogliamo la x positiva):
2x= y+1
E dividiamo tutto per 2:
x= \frac{y+1}{2}
Abbiamo così ricavato x=^{-1}(y) . Adesso dobbiamo scambiare il nome degli assi, cioè scambiamo x con la y e viceversa:
y= \frac{x+1}{2}
E questa è la funzione inversa y=^{-1}(x) .
Vediamo altri esempi più specifici.
Funzione inversa di una fratta
Esempio 2. Troviamo la funzione inversa di y= \frac{1}{x+1} .
Moltiplichiamo tutto per x+1 per eliminare la frazione:
y(x+1)= \frac{1}{x+1} (x+1)
La frazione si semplifica:
y(x+1)= 1
Dividiamo per y:
x+1= \frac{1}{y}
x= \frac{1}{y} -1
Trovata la x=^{-1}(y) , adesso scambiamo x con y e viceversa, ed i giochi sono fatti.
y= \frac{1}{x} -1
Che è y=^{-1}(x) . Vi mostriamo anche il grafico.
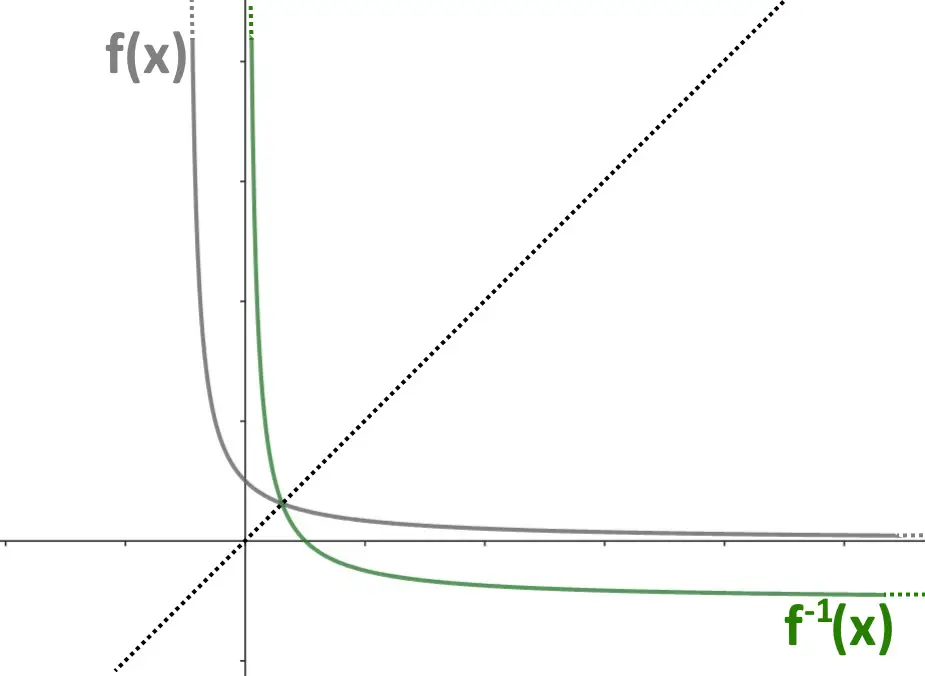
f(x) inversa del logaritmo
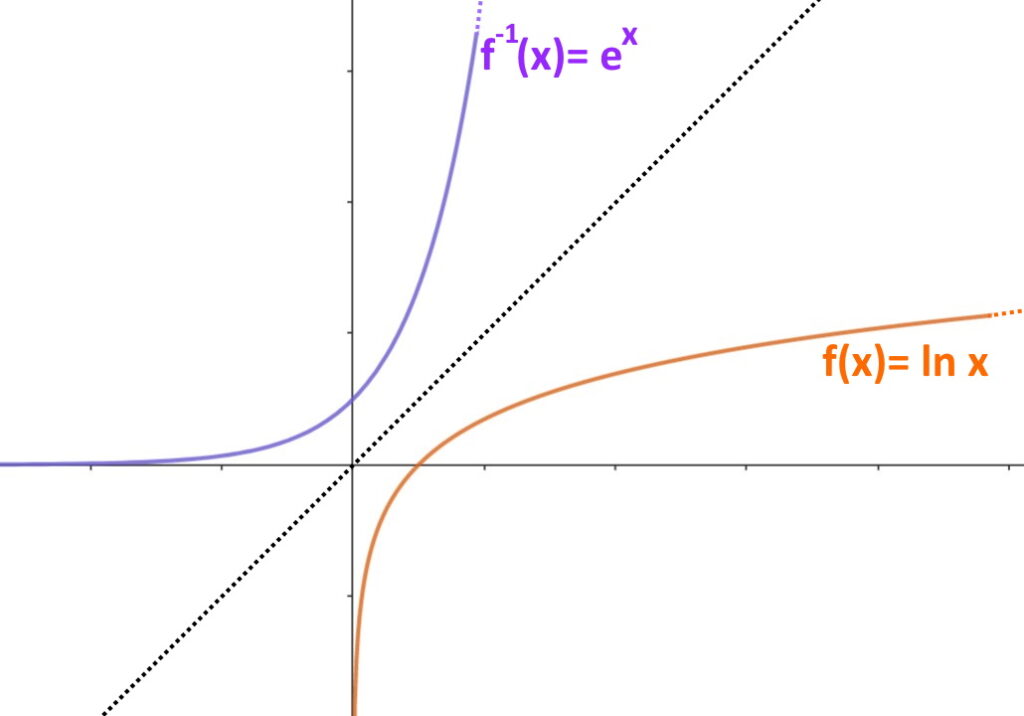
Esempio 3. Troviamo l’inversa di y= \ln x .
Per far ciò sfruttiamo una formula importantissima nelle equazioni logaritmiche:
\log_a b = c \implies b = a^c
Quindi nel nostro caso :
x= e^y
Scambiamo il nome degli assi:
y= e^x
Ed abbiamo ottenuto l’esponenziale! Di fatti l’esponenziale è l’inversa della funzione logaritmica!
f(x) inversa del seno
Questo è un esempio importante perché operiamo una restrizione del dominio.
Esempio 3. Troviamo l’inversa di y= \sin x .
La funzione seno si presenta nel modo seguente, e di conseguenza non è biettiva. (Per ogni y ci sono infinite x)
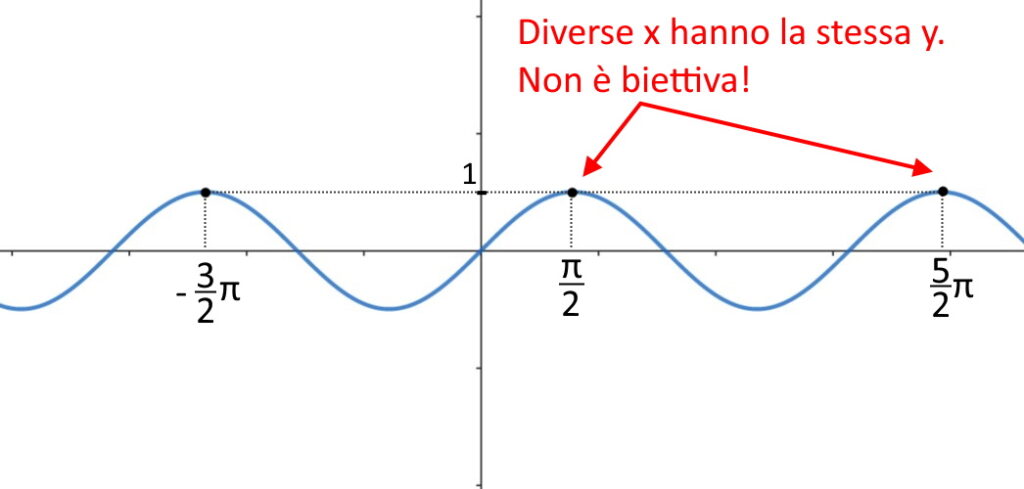
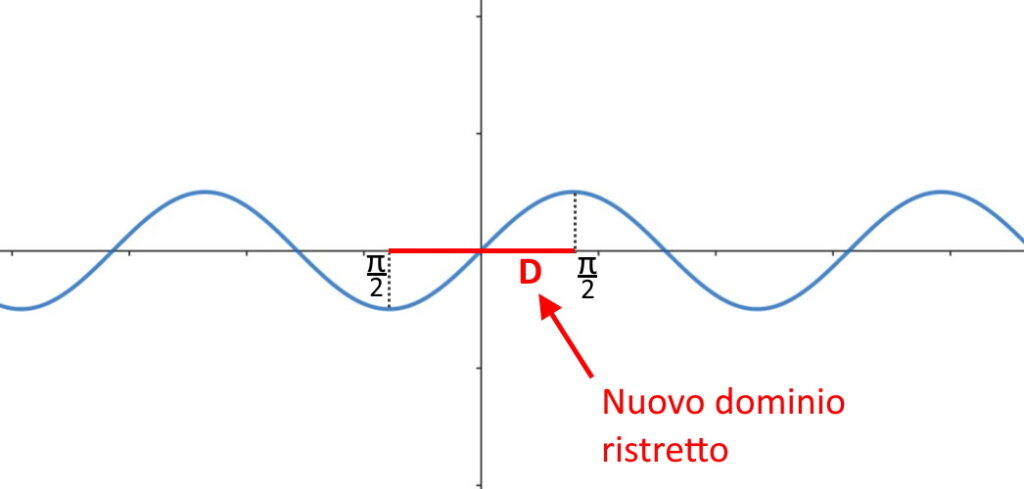
Non è possibile trovare la sua inversa. Quindi operiamo una restrizione del dominio. Ossia se prima la funzione era definita in tutto R, cioè in ]-\infin , + \infin [ , ci concentriamo sulla funzione solamente nell’intervallo [- \frac{\pi}{2} , \frac{\pi}{2}] .
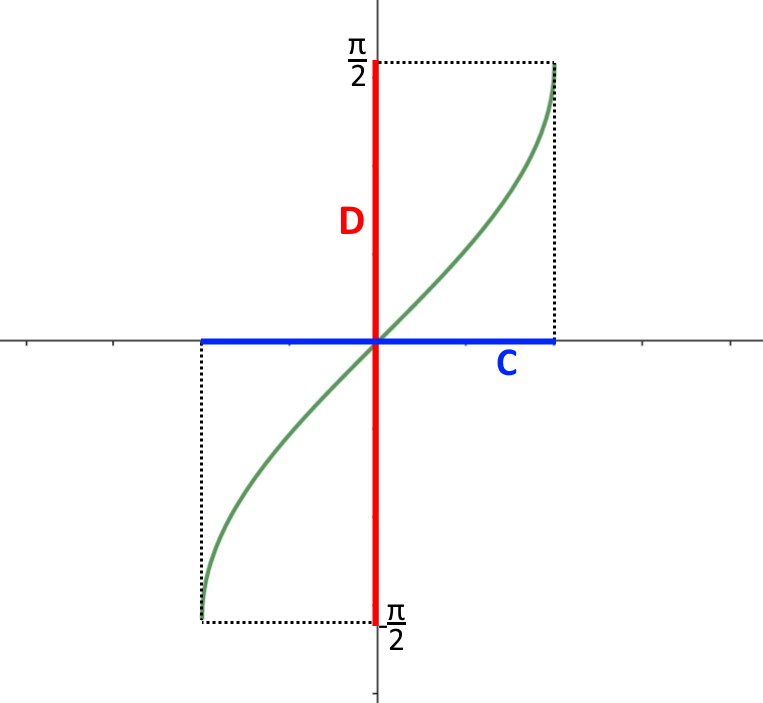
E da qui l’inversa. Non ci sono calcoli da fare perché si definisce a parte la f^{-1} {/katex]: [katex]y= \arcsin x
Vediamo di approfondire il discorso, riguardo adesso la continuità dell'inversa.
Continuità della funzione inversa
Se ho una funzione f, la sua inversa f^{-1} è continua? Sì, c'è un teorema che garantisce la continuità anche della sua inversa.
La pagina è conclusa. Trovate sul nostro sito centinaia di altri argomenti sia di matematica, che di geometria analitica e geometria!
Continuate a supportare il nostro sito!
Per approfondire:
https://it.wikipedia.org/wiki/Funzione_inversa
crescenti
decrescenti
pari e
dispari