Funzione pari e dispari: definizione ed esempi
Funzione pari e dispari: definizione ed esempi! In questa pagina andremo a vedere la definizione di funzione pari e di funzione dispari, vedremo inoltre delle applicazioni, esempi svolti e come capire se una funzione è pari o dispari (in termini pratici e di esercizi). Questo fa parte dello studio delle simmetrie di una funzione: cosa super utile soprattutto quando si andrà a fare lo studio di una funzione.
Indice
- Funzione pari
- Esempi di funzioni pari
- Funzione dispari
- Esempi di funzioni dispari
- Come capire se una funzione è pari o dispari?
- Operazioni con simmetrie
Partiamo subito col vedere cosa significa e che cosa è una funzione che è pari!
Funzione pari
Consideriamo una funzione f(x) definita in un certo dominio D. Una funzione si dice pari se:

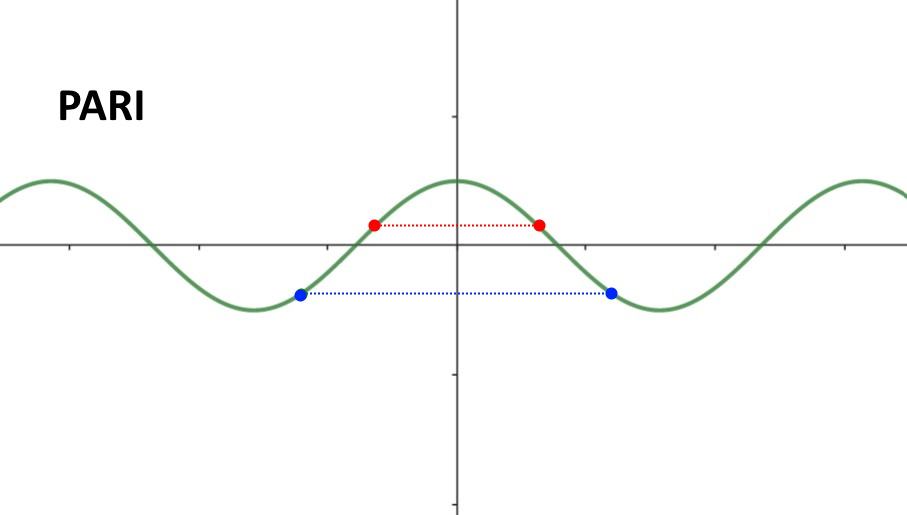
Cosa significa in termini pratici? In pratica, quando una funzione è pari allora è simmetrica rispetto all’asse y. Cioè la parte destra del grafico della funzione è specchiata rispetto alla parte sinistra.
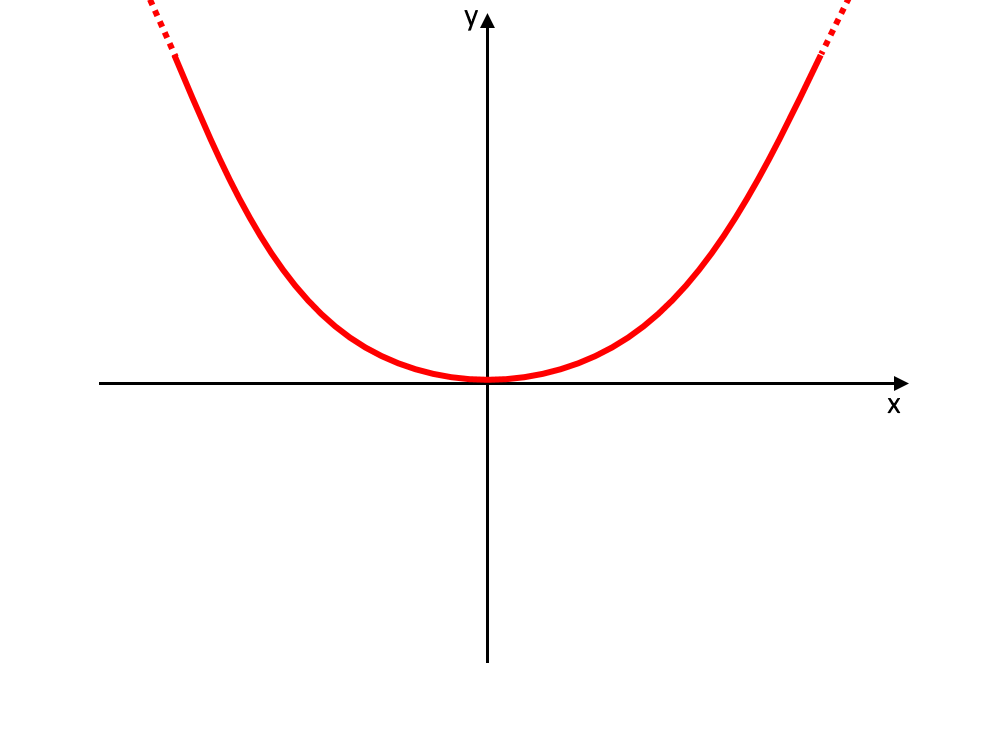
Perché si dice specchiata e non uguale? Le due parti del grafico sono specchiate, non sono uguali, altrimenti sarebbe così come segue.
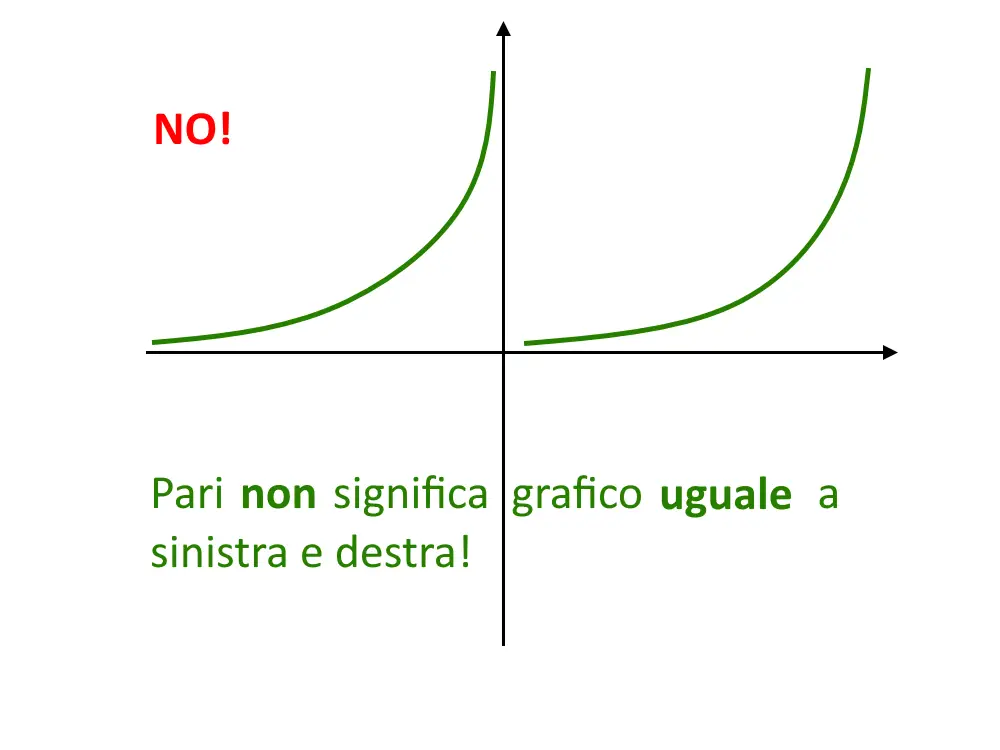
Invece si dice che è specchiata, perché è come se ci fosse uno specchio sull’asse y! Di fatti se prendiamo il punto del grafico ad esempio P=(3,7) nella parte destra, esisterà il punto specchiato P' = (-3,7) . Questo punto P’ lo si può trovare andando a disegnare un segmento orizzontale che passa per l’asse y. Tale segmento è lungo uguale nella parte sinistra e destra.
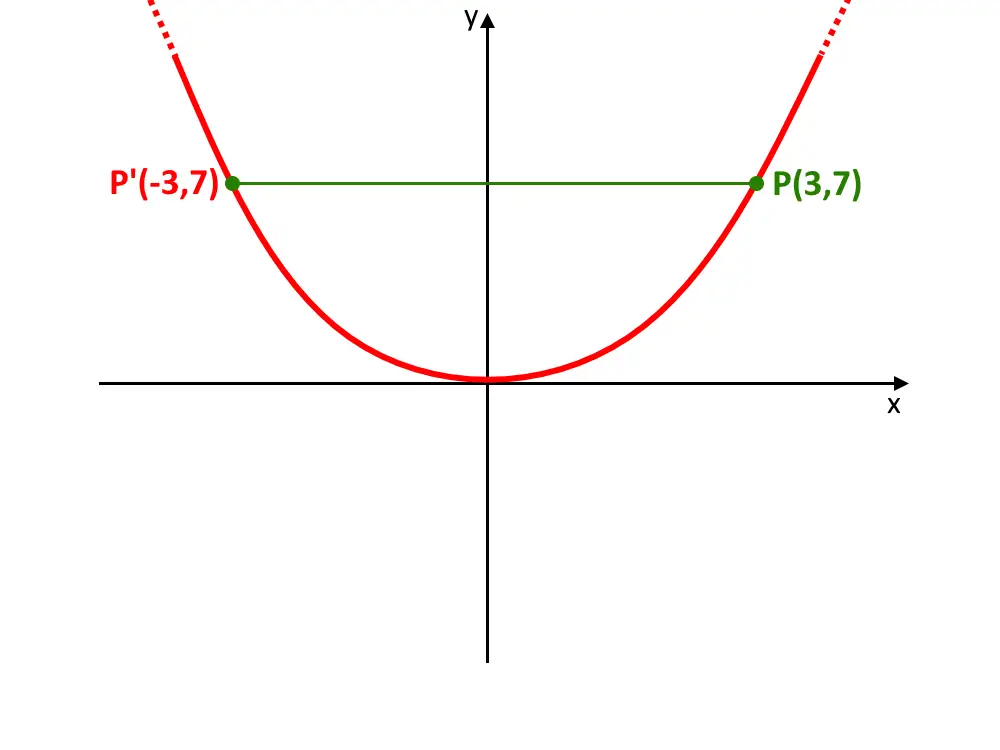
Questa è una vera e propria proprietà di simmetria! Perché è importante? E’ importante sapere cosa significa perché se dovete disegnare il grafico di f(x) e vi dicono che la funzione è pari, allora basterà studiare e disegnare solo la parte destra ad esempio, così vi risparmiate molti inutili conti!
Perché solo la parte destra? Perché una volta studiata e disegnata la parte destra (la parte più semplice visto che avete x positivo), vi basta disegnare a sinistra un grafico specchiato di quello destro!
In generale per molti argomenti, quando c’è una simmetria come la parità, è sinonimo di fare meno conti!
Vediamo ora alcuni esempi di funzioni pari! (Alla fine della pagina ci saranno esercizi sul come capire se una funzione è pari).
Esempi di funzioni pari
La funzione f(x) = x^2 ad esempio è pari! Guardate il grafico suo: la parte destra è uguale a quella sinistra ma specchiata!
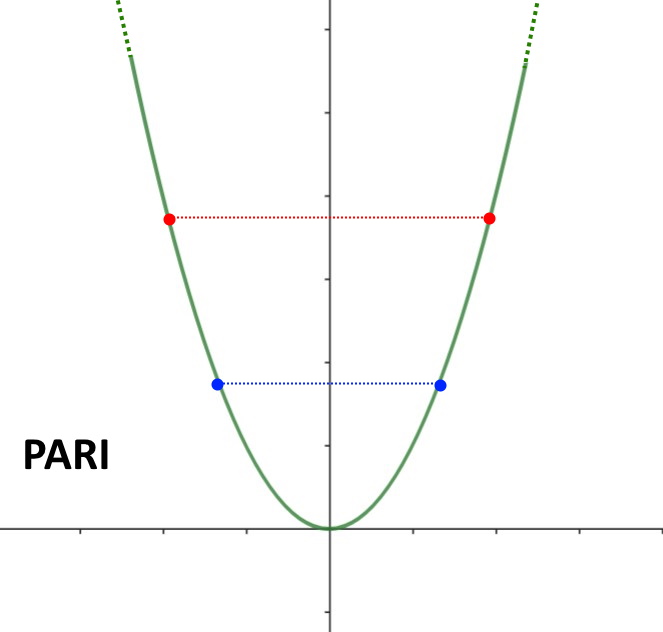
Un altro esempio di funzione pari è ad esempio f(x) = \cos x .
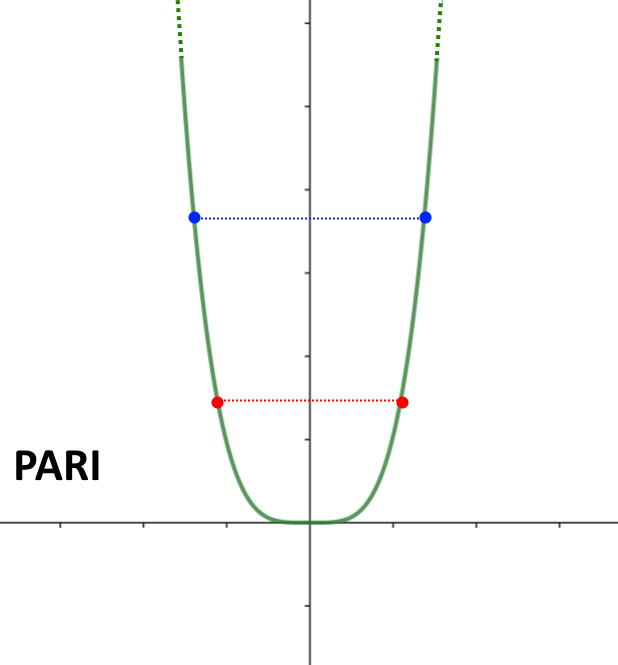
O ancora anche la funzione f(x) = x^4 è pari. In generale tutte le funzioni con esponente pari lo sono.
Vediamo ora cosa significa che una funzione è dispari, poi alla fine vedremo degli esercizi.
Funzione dispari
Consideriamo sempre una funzione f(x) definita nel dominio D. Tale funzione si dice dispari se:

La simmetria adesso è rispetto all’origine degli assi cartesiani. Una funzione dispari è un qualcosa di questo tipo.
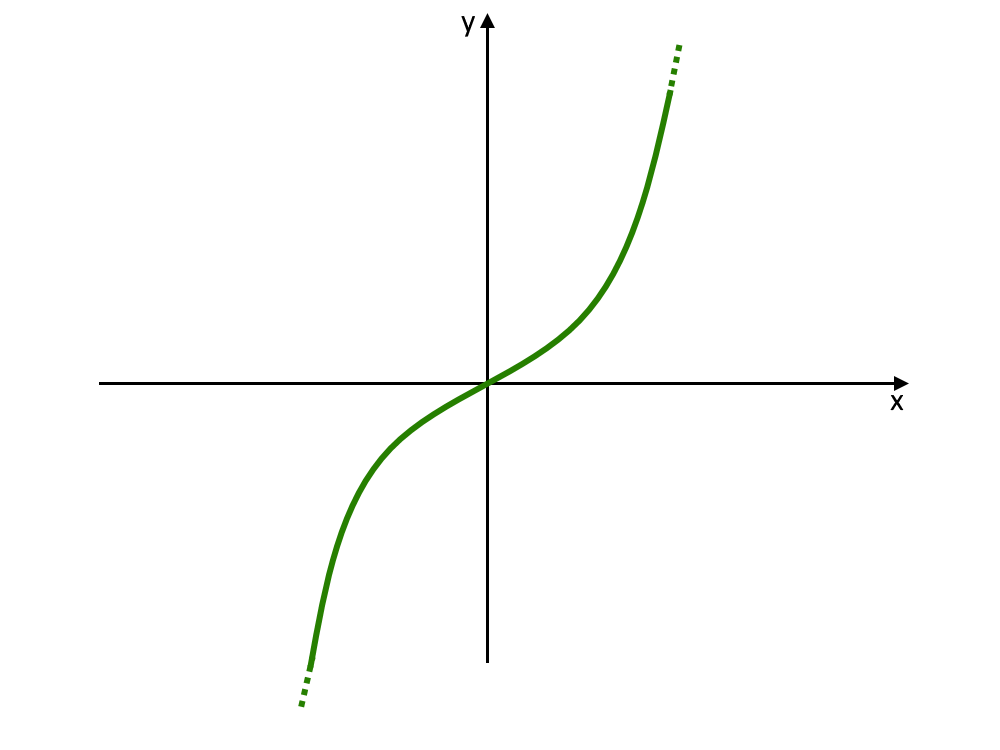
Questo cosa vuol dire? La simmetria questa volta è rispetto all’origine degli assi cartesiani. Qui il discorso è leggermente diverso, ma ve lo spiegherò. Se prima avevamo una simmetria rispetto ad un asse, adesso è rispetto ad un singolo punto. Questo significa che se prendete un punto ad esempio P = (3,8) a destra del grafico, per trovare il suo punto simmetrico a sinistra: dobbiamo tracciare un segmento che passa per l’origine. Tale segmento è lungo uguale a destra e sinistra. Il punto simmetrico risulta essere P' = (-3,-8) .
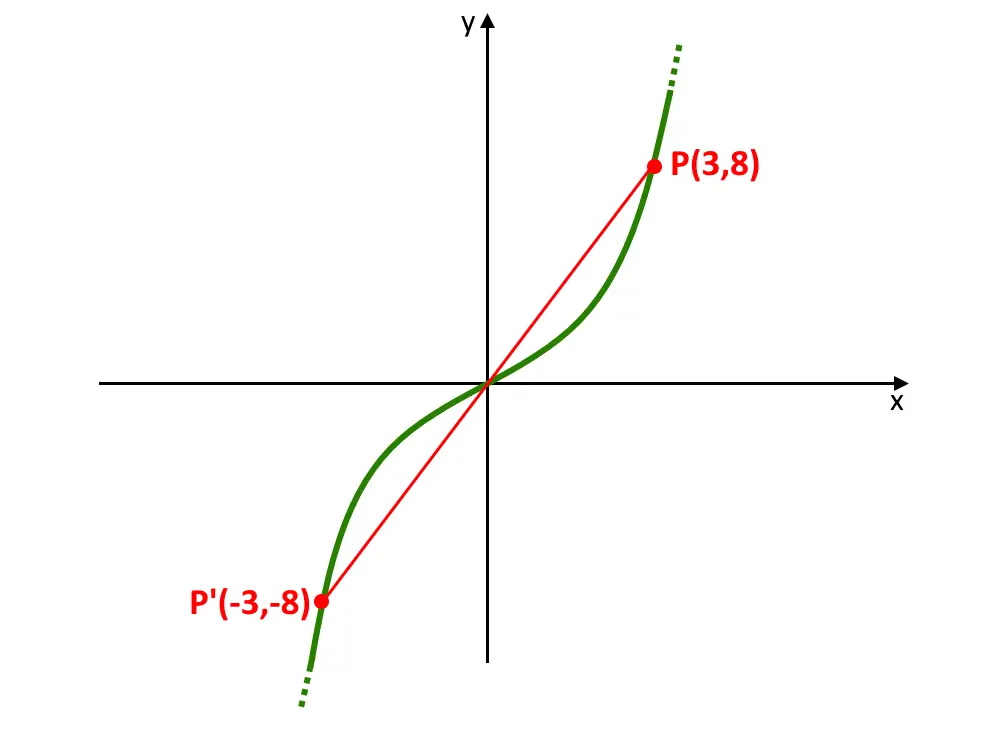
Anche questa è una simmetria, quindi vi può semplificare i conti di alcuni esercizi, soprattutto di grafici!
Vediamo degli esempi di funzioni dispari. Alla fine della pagine vedremo degli esercizi pratici sul come capire se una funzione è dispari.
Esempi di funzioni dispari
Sono dispari tutte le funzioni con esponente dispari, come f(x) = x^3 . Di fatti:
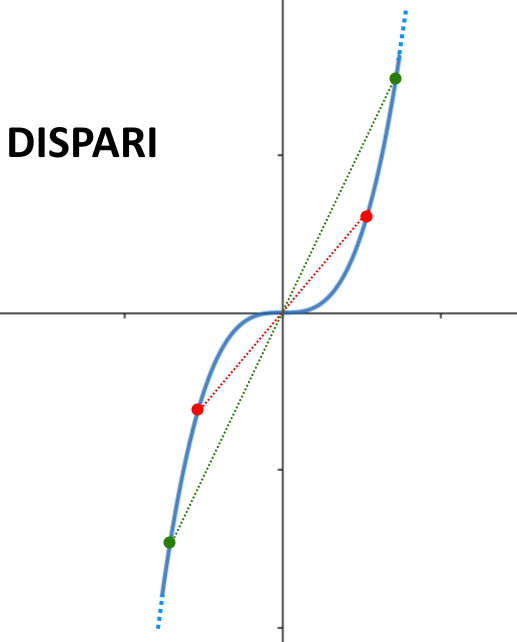
Per le funzioni goniometriche abbiamo il seno f(x) = \sin x che è dispari.
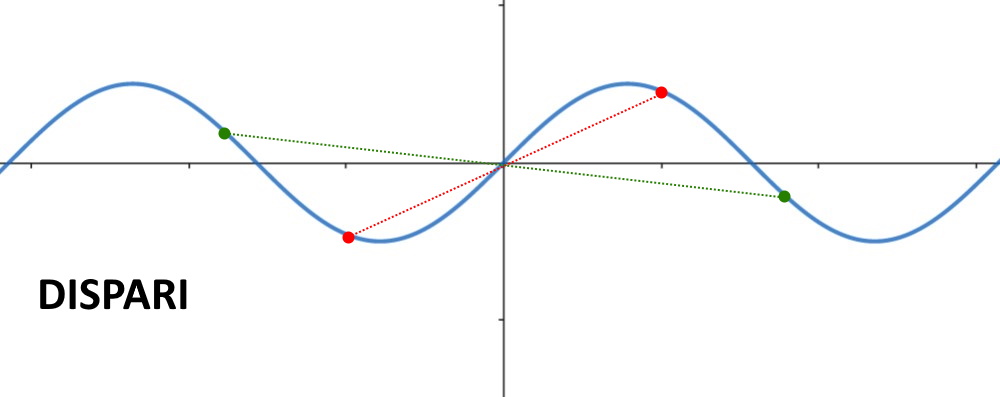
O anche stesso f(x) = x , questo non è facile da notare per esempio.
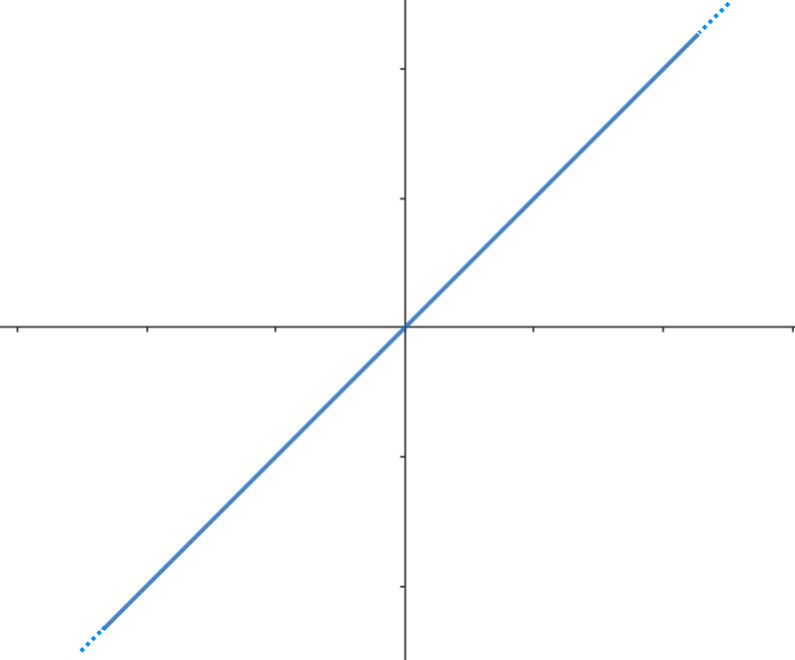
Vediamo adesso in senso pratico come facciamo a capire, con calcoli, se una funzione è pari o dispari!
Come capire se una funzione è pari o dispari
Esercizio 1. Capire la simmetria della funzione f(x) = x^2 + 9 .
Per studiare la simmetria di una funzione bisogna sostituire -x alla x della funzione, e si vede cosa esce.
- Se sostituendo -x esce fuori che f(-x)=f(x), allora la funzione è pari;
- Se sostituendo -x esce fuori f(-x)= -f(x), allora la funzione è dispari.
- Altrimenti, la funzione non ha simmetrie.
Quindi come prima cosa andiamo a sostituire il valore di -x:
f(-x) = (-x)^2 + 9
Essendo che abbiamo messo -x, allora bisogna scrivere f(-x) all’inizio. Comunque, visto che si ha un quadrato, ciò che esce è positivo:
f(-x) = x^2 + 9
Quello che possiamo notare è che otteniamo lo stesso valore della funzione iniziale dell’esercizio.
Di conseguenza f(x) = f(-x).
La funzione è quindi pari. Di fatti il grafico di questa è il seguente.
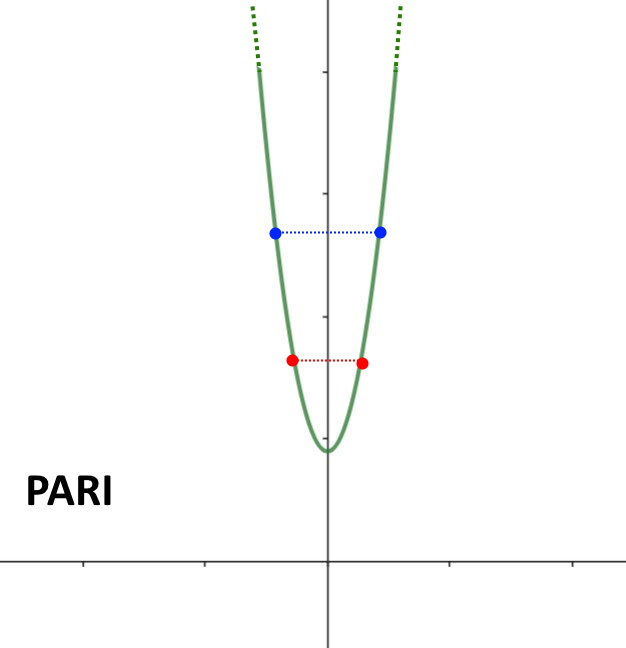
Esercizio 2. Capire la simmetria della funzione f(x) = \frac{ \sqrt{1 -4x^2} }{x} .
Sostituiamo al posto della x, il valore di -x. Mettete le parentesi come facciamo noi, che è facile confondersi!
f(-x) = \frac{ \sqrt{1 -4(-x)^2} }{-x}
Il quadrato riporta il valore positivo:
f(-x) = \frac{ \sqrt{1 -4x^2} }{-x}
Il meno lo possiamo anche portare davanti alla frazione:
f(-x) =- \frac{ \sqrt{1 -4x^2} }{x}
Quello che possiamo notare è che abbiamo ottenuto esattamente la stessa funzione f(x)=f(-x) (guardate la traccia dell’esercizio, la funzione è uguale) ma con un segno meno davanti! La funzione è quindi dispari. Il grafico di questa funzione è la seguente infatti.
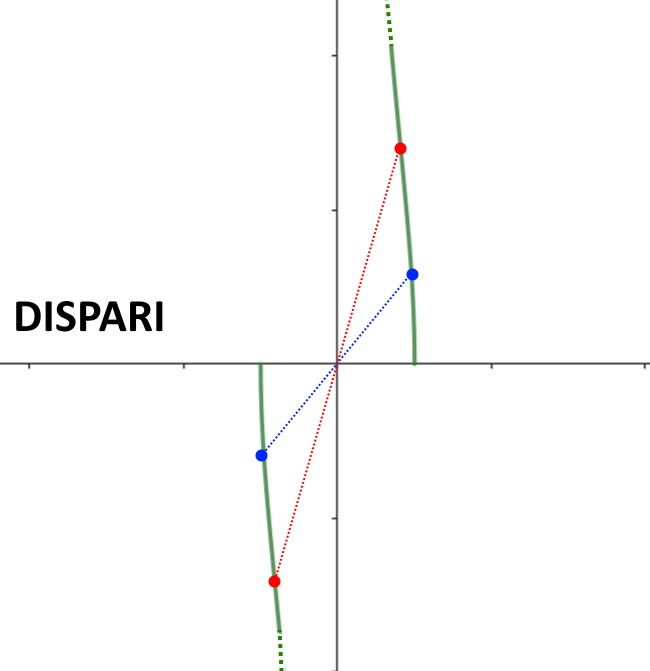
Esercizio 3. Capire la simmetria della funzione f(x) = 2 |x| -x .
Sostituiamo quindi al posto della x, il valore di -x:
f(-x) = 2 |-x| - (-x)
Il valore assoluto di un numero negativo, è un numero positivo. Poi il meno davanti alla parentesi fa sì che esca +. Otteniamo:
f(-x) = 2 |x| +x
Questa funzione non è uguale a quella iniziale. Inoltre notiamo che non è neanche di segno opposto (dispari). Di fatti se prendiamo la funzione iniziale e ci mettiamo un segno meno, avremmo dovuto ottenere:
f(x) = -(2 |x| -x) = - 2|x| +x
Ma non abbiamo neanche ottenuto questo. La funzione non ha simmetrie.
Esercizio 4. Capire la simmetria della funzione f(x) = x^2 - 2 |x| + 6 .
Sostituiamo la -x:
f(-x) = (-x)^2 - 2 |-x| + 6
Il quadrato ridà il valore positivo, e stessa cosa anche il valore assoluto:
f(-x) = x^2 - 2 |x| + 6
E’ proprio la stessa! La funzione è pari.
Esercizio 5. Capire la simmetria della funzione f(x) = \sqrt{-x^2 -6x} + \sqrt{ -x^2 +6x} .
Con la solita sostituzione ricaviamo che:
f(x) = \sqrt{-(-x)^2 -6(-x)} + \sqrt{ -(-x)^2 +6(-x)}
f(x) = \sqrt{-x^2 +6x} + \sqrt{ -x^2 -6x}
La funzione è la stessa, semplicemente c’è prima un termine e poi l’altro invertiti. Ma è uguale per via della proprietà commutativa: cioè 1+3 = 3+1.
La funzione è pari quindi.
Vediamo ora come possiamo semplificare e velocizzare la ricerca delle simmetrie!
Operazioni con simmetrie
Fra le due simmetrie c’è un legame. Si possono risolvere gli esercizi precedenti più velocemente, conoscendo le operazioni con simmetrie.

Così è tutto più semplice! Di fatti se dobbiamo capire la simmetria di f(x) = x \cdotp \sin x + x basta fare questo ragionamento molto veloce:
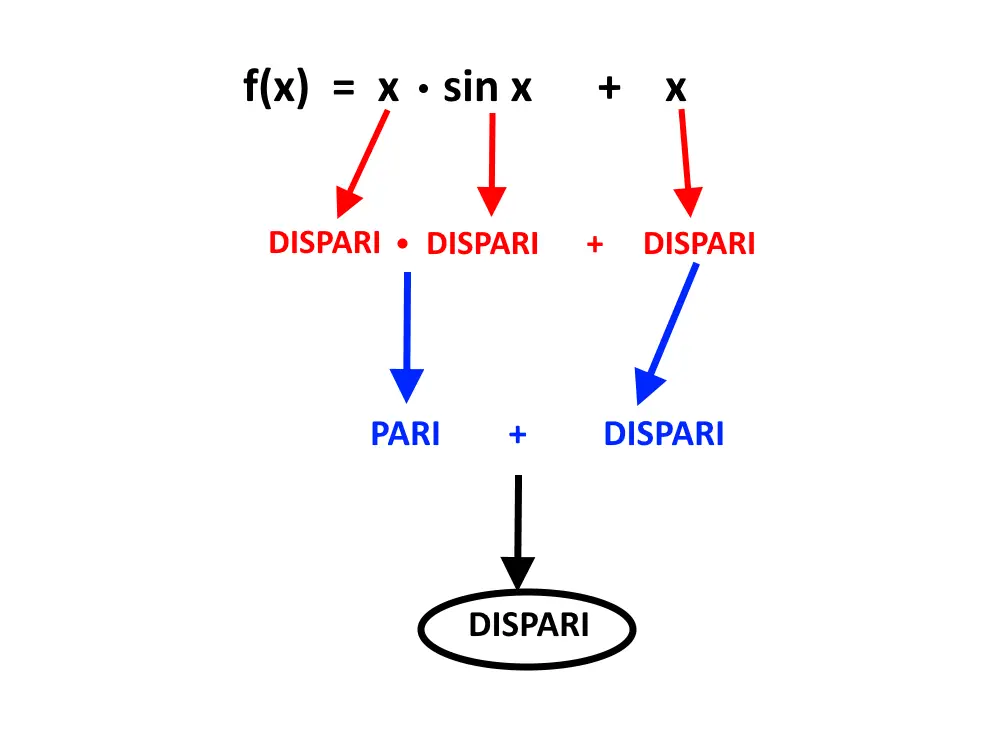
Ed ecco fatto!
Trovate sul nostro sito centinaia di esercizi svolti e argomenti di matematica, geometria analitica e geometria!
Continuate a supportarci!
Per approfondire:
https://it.wikipedia.org/wiki/Funzioni_pari_e_dispari#:~:text=In%20matematica%2C%20le%20funzioni%20pari,e%20delle%20serie%20di%20Fourier.
inversa
composta