Equazioni TERZA MEDIA: spiegazione e 20 ESERCIZI SVOLTI

In questa pagina spiegheremo tutto delle equazioni per la terza media: dal cosa sono, le regole da rispettare ed arriveremo al come si risolvono. Alla fine della pagina ci saranno tantissimi esercizi spiegati in ogni singolo passaggio, così che non avrete dubbi su ciò che dovete fare! Imparare le equazioni, alla terza media è fondamentale, poiché sono anche un argomento centrale all’esame di terza media! Iniziamo subito ragazzi.

Indice

• Cosa sono le equazioni
• Come si risolvono le equazioni
• ESERCIZI svolti e spiegati
• Equazioni con frazioni
• Equazioni difficili

Detto questo, iniziamo subito a vedere cosa sono le equazioni e quale è l’obiettivo delle equazioni in terza media.

Cosa sono le equazioni (spiegazione per terza media)

Prima di entrare nel vivo degli esercizi, vediamo cosa sono le equazioni, per chi non lo sapesse. Una equazione è una espressione (numeri con operazioni matematiche) in cui c’è anche una incognita “x”. Iniziamo subito a mostrare un esempio di equazione, e poi lo commenteremo e capiremo meglio.

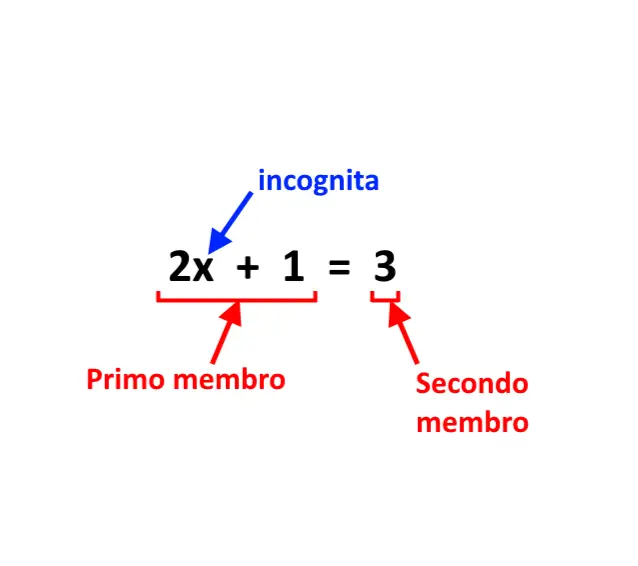
Questa sopra è una equazione. Una equazione è formata dai seguenti elementi:

• Primo membro (i numeri ed i termini che stanno a sinistra dell’uguaglianza)
• Secondo membro (i numeri ed i termini che stanno a destra dell’uguaglianza)
• Incognita (è la “x” che non si conosce, e la si deve trovare)
• Uguaglianza (=)

Questi sono gli elementi che contraddistinguono una equazione.

Sì abbiamo capito, ma chi è la incognita “x”? L’incognita “x” è un numero che non si conosce, all’inizio. L’obiettivo delle equazioni è infatti trovare il numero che si nasconde dietro la “x”!

Quindi è come se stessimo mettendo una mano sopra un numero di una uguaglianza, e l’esercizio consisterà nel trovare come si nasconde dietro!

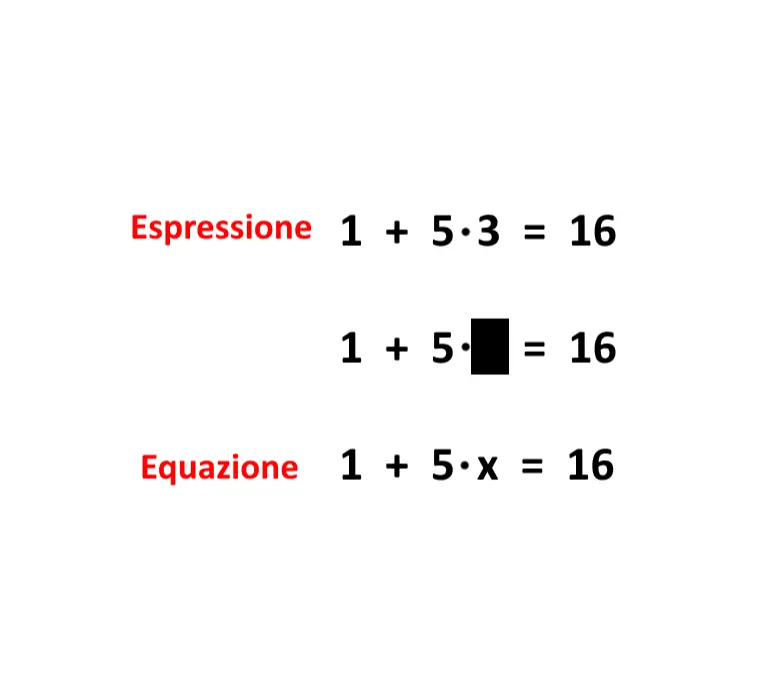
Il numero che si trova dietro la “x” si chiama “soluzione” dell’equazione.

Come si risolvono le equazioni

Nel primo paragrafo abbiamo introdotto e capito cosa sono le equazioni. Prima di vedere come si risolve una equazione, dobbiamo mostrarvi alcune regole di risoluzione (IMPORTANTISSIME!), quindi leggete con calma e prendete appunti!

La prima regola che vale è che possiamo portare un numero da una parte all’altra dell’equazione (da sinistra a destra, o da destra a sinistra) semplicemente cambiando il segno del numero!

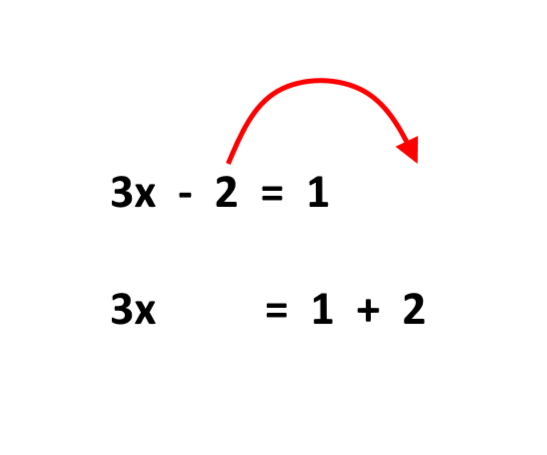
Perché questo è possibile? Perché possiamo farlo? Una uguaglianza vale anche se addizioniamo ad entrambi i membri uno stesso numero, come nel seguente esempio.

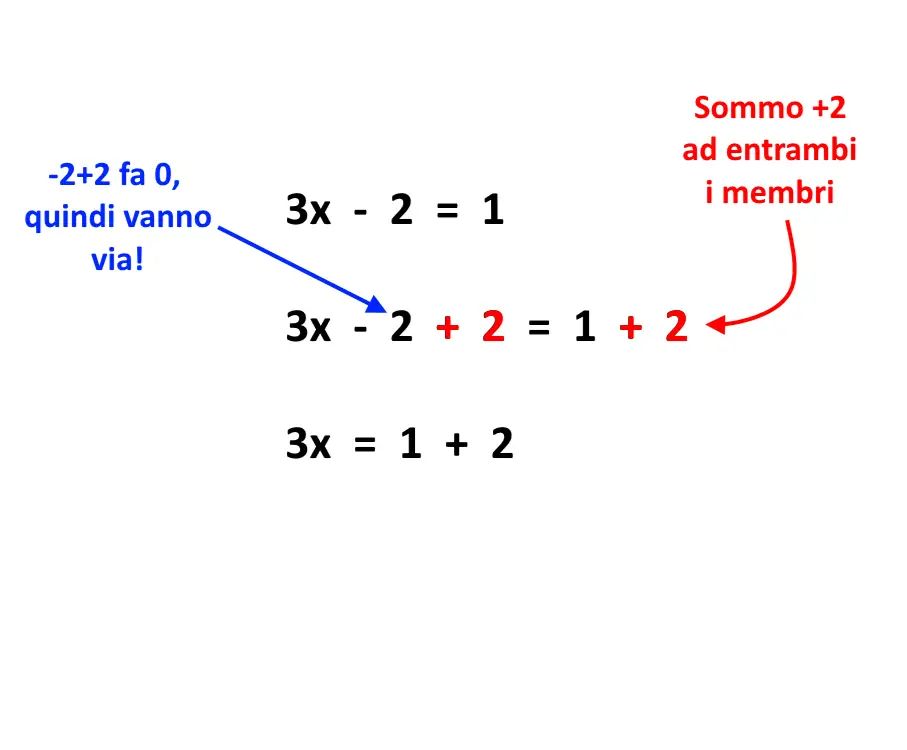
Nell’equazione di prima, aggiungendo +2 ad entrambi i membri, esce fuori proprio che il numero spunta fuori dal lato opposto, ma cambiato di segno!

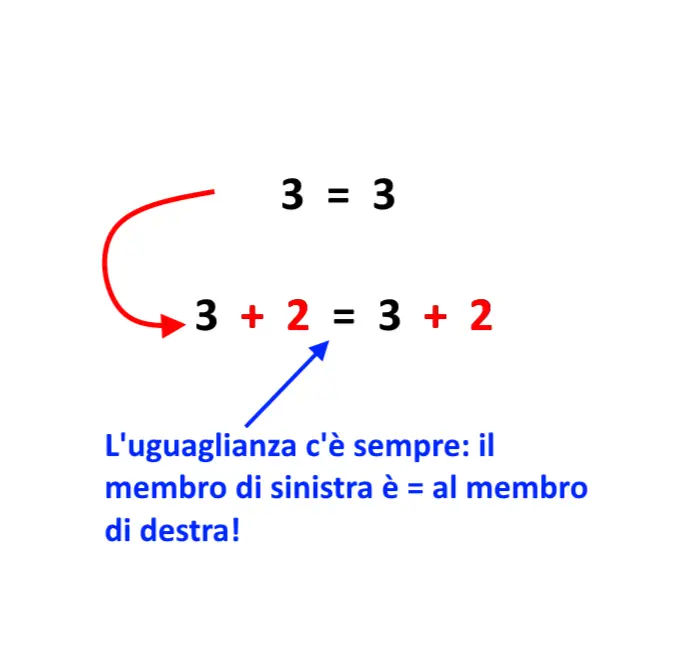
Questa regola è di fondamentale importanza! E la si usa in ogni singolo esercizio. Questa regola vale anche per la “x”? Sì, assolutamente. Ecco un esempio.

Passiamo adesso alla seconda regola, anche questa regola che viene usata in ogni esercizio! Importantissima anche questa. Ciò che è stato detto, vale anche quando si moltiplica o si divide tutto per uno stesso numero. Cioè, a volte potrebbe esserci bisogno (per trovare la x) di dividere tutto per un numero, e lo si può fare!

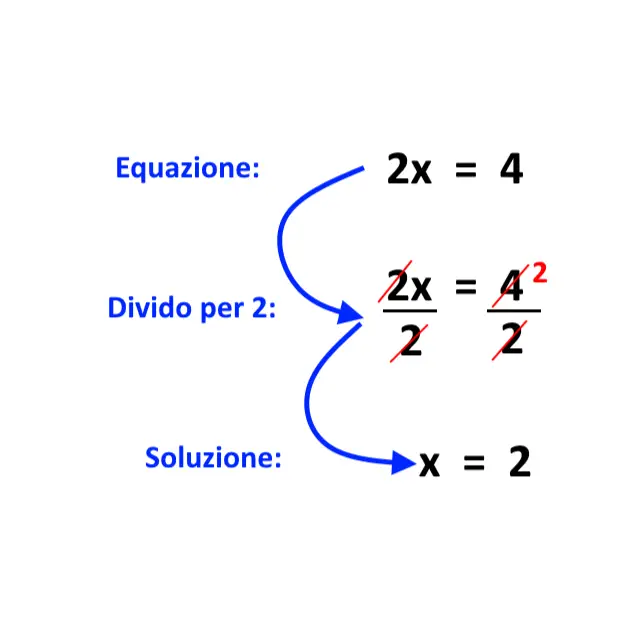
Come già state intuendo, queste regole servono per cercare di ricavare la “x” e basta, a sinistra.

Vediamo adesso l’ultima regoletta importante. Nelle equazioni possono comparire più termini con le x, e questi bisogna sommarli! Come si sommano due termini (ad esempio 2x + 3x)? Il risultato di questa somma ci darà x, preceduto da 2+3=5!

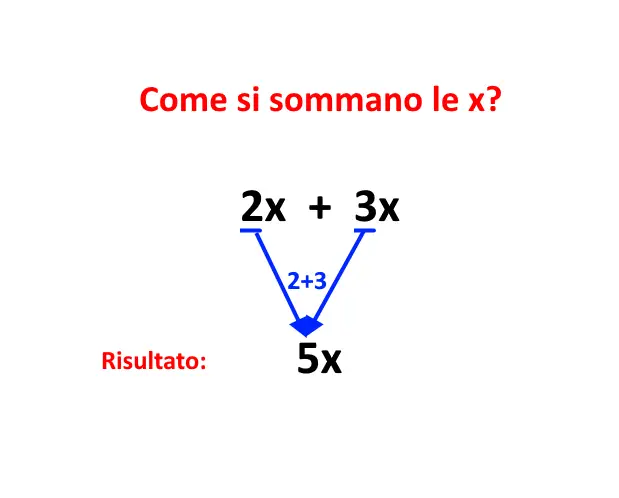
Abbiamo finito di vedere queste tre regolette importanti, ora passiamo alla risoluzione di una equazione.
Adesso vediamo la cosa più importante, come trovo la x? Per trovare a cosa è uguale la x, devo arrivare ad averla a sinistra da sola, ed a destra un solo numero.

Per arrivare a giungere a questa forma, useremo le tre regole che vi abbiamo introdotto!

Abbiamo capito che risolvere una equazione significa trovare la x. Come si fa? Il procedimento di risoluzione di una equazione si può riassumere nei seguenti passaggi principali.

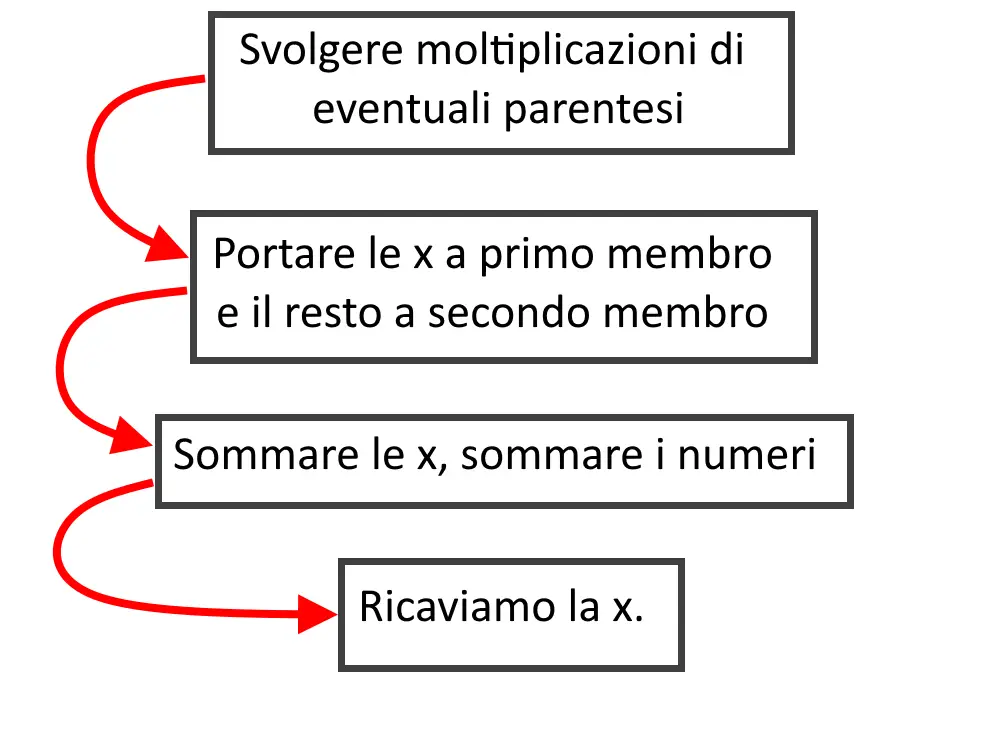
Commentiamo questi passaggi:

• Il primo passaggio consiste nel semplificare la forma dell’equazione che abbiamo. Finché non leviamo le parentesi e facciamo le operazioni che compaiono in una equazione non si può andare avanti
• Il secondo passaggio consiste nell’iniziare a portare tutte le “x” che ci sono a sinistra, nel primo membro (ce ne possono essere di più che vanno sommate fra di loro), nel frattempo si portano i numeri a destra.
• Il terzo punto consiste nell’effettuare le somme (come 3+2 e scriviamo 5, oppure se c’è scritto 2x+x scriviamo 3x)
• Il quarto punto consiste nell’avere a sinistra SOLO la x! E l’equazione è risolta.

Discutiamo adesso delle soluzioni che possono uscire.

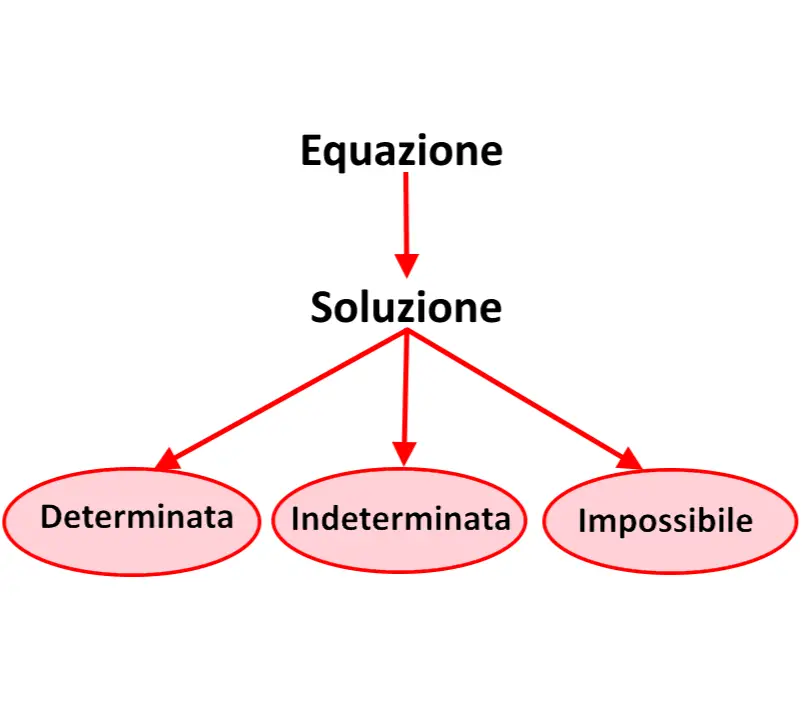
Purtroppo non sempre abbiamo come soluzione della “x” un numero (in questo caso la soluzione si dice determinata). Ci sono due casi in cui la soluzione può essere “indeterminata” e “impossibile”. Ora vediamo le diverse soluzioni che possiamo avere.

Si ha una soluzione impossibile quando la “x” scompare, come nel seguente esempio:

3x + 2 = 3x

Portiamo il 3x da destra a sinistra (vogliamo tutte le x a sinistra):

3x -3x +2= 0

A destra non rimane niente, quindi scriviamo 0. Dopo di che come possiamo vedere, sommando 3x-3x esso fa zero, quindi:

+2= 0

La “x” è scomparsa! In questo caso l’equazione si dirà impossibile.

Abbiamo una soluzione della “x” indeterminata, invece, quando scompare sia la “x” che il numero! Vediamo un esempio subito per capire:

2x +1 -1 = 2x

Portiamo il 2x a sinistra:

2x -2x +1 -1 = 0

Come possiamo vedere si cancellano sia i numeri, che le x. La soluzione si dirà indeterminata!

Abbiamo quindi capito in toto le equazioni, adesso cerchiamo di andare sul pratico, vediamo quindi come svolgere degli esercizi!

Equazioni esercizi svolti (terza media)

Esercizio 1. 2x -3 = -5


Prima di partire con la risoluzione, osserviamo l’equazione: non ci sono parentesi né calcoli da fare. Passiamo dunque al tenere la x a sinistra (il 2x sta già a sinistra), e poi i numeri a destra (portiamo il -3 a destra, ricordandoci sempre di cambiare il suo segno):

2x = -5+3

Come potete vedere il -3 portato a destra è diventato +3! Adesso svolgiamo quella somma al secondo membro che compare. Se non sapete farla, prendete la calcolatrice!

2x = -2

L’obiettivo di una equazione, non dimentichiamolo mai, è trovare la x. Vogliamo solo la x e basta. Notiamo che c’è un 2 attaccato alla x, e lo vogliamo levare di mezzo. Come facciamo? Dividiamo tutto (entrambi i membri) per 2:

\frac{2x}{2} = - \frac{2}{2}

Il 2 al numeratore ed al denominatore si semplifica. Quindi avremo:

x = - 1

Neanche ci siamo accorti che…abbiamo risolto l’equazione! Abbiamo trovato a quale valore è uguale la x, e quindi abbiamo concluso l’esercizio!

Esercizio 2. -x + 4 = 7x


Anche in questo secondo esercizio non ci sono calcoli da fare (ve li facciamo vedere negli esercizi più avanti), quindi osserviamo l’equazione: abbiamo da portare il 7x a sinistra. Facciamolo:

-x + 4 -7x = 0

P.S: Quando portiamo un numero o una x da un lato, e non rimane più niente come in questo caso, si scrive lo 0.

Adesso portiamo i numeri a destra, al secondo membro!

-x -7x = -4

Al primo membro c’è da effettuare una bella somma. Dall’altro lato non c’è niente da fare:

-8x = -4

Se non sapete fare (-1-7 fatelo alla calcolatrice per essere sicuri). Notiamo che c’è un 8 attaccato alla x, quindi dividiamo tutto per 8 appunto.

- \frac{8x}{8} = - \frac{4}{8}

Semplifichiamo ed otteniamo:

- x = - \frac{1}{2}

Abbiamo finito? Purtroppo ancora no, è rimasto un segno – davanti alla x. Noi vogliamo sempre e solo la x isolata! Come si leva un segno meno? Si moltiplica tutto per -1:

-1 \cdotp - x = -1 \cdotp - \frac{1}{2}

Moltiplicare per -1, in breve, fa cambiare di segno e basta! (meno per meno fa più)

x = \frac{1}{2}

Esercizio 3. 6x - 26 = 16x -56


Qui abbiamo un esercizio già con più termini e numeri. Quando si complicano le cose, facciamo sempre un passaggio alla volta. Iniziamo per esempio a portare il 16x a primo membro:

6x - 26 -16x = -56

Ora nel passaggio successivo pensiamo a portare il -26 dall’altro lato:

6x -16x = -56 +26

Procediamo a sommare:

-10x = -30

Dividiamo tutto per 10:

- \frac{10x}{10} = - \frac{30}{10}

Semplifichiamo:

- x = - 3

Ed ora come prima, moltiplicando tutto per -1 (lo potete anche fare a mente) si cambia tutto di segno. Quindi senza scrivere ogni volta che moltiplichiamo per -1, possiamo anche dire direttamente “cambio tutto di segno”:

x = 3

In questa scorciatoia ci dobbiamo ricordare di cambiare il segno a TUTTI i termini e numeri che compaiono in TUTTA l’equazione!

Continuiamo con altri esercizi di equazioni di terza media!

Esercizio 4. -8x + 5 = 5 -8x


Non skippate questo esercizio! Vedremo una soluzione molto particolare! Dai precedenti esercizi svolti, avrete capito come si fanno le equazioni, provate quindi da soli e poi tornate qui! Iniziamo a portare le x a sinistra:

-8x + 5 +8x = 5

E poi d’altra parte:

-8x +8x = 5 -5

Ora che sommiamo, notiamo qualcosa di strano.

0x = 0

Ed ora? Questa è la forma di una equazione, la cui soluzione è “indeterminata”. Quando avete questo risultato, sapete ora che soluzione mettere!

Soluzione si dice indeterminata poiché non si può trovare un risultato definito ed unico.

Esercizio 5. 3( 7x-5 ) =15x -1


Ora iniziano a complicarsi le cose: ci sono dei calcoli da fare. La logica che abbiamo seguito fino ad ora vale solo quando non dobbiamo prima fare dei calcoli (moltiplicazioni o parentesi da levare).

Quindi, prima di andare avanti, la prima cosa da fare è svolgere quella moltiplicazione fra il 3 e la parentesi. Se non vi ricordate vi rammentiamo noi: il 3 va a moltiplicarsi con ogni termine dentro la parentesi:

3 \cdotp 7x- 3 \cdotp 5 =15x -1

21x- 15 =15x -1

Fatto questo calcolino iniziale, procediamo con i soliti passaggi che ormai avrete imparato benino!

21x-15x =-1 +15

Sommiamo:

6x = 14

Adesso dividiamo semplicemente per 6:

x = \frac{14}{6}

Possiamo sicuramente semplificare quella frazione, dividendo numeratore e denominatore per 2:

x = \frac{7}{3}

Ed abbiamo finito 🙂

Esercizio 6. 8( x+3 ) = 8x -24


Questo esercizio è importante: NON SKIPPARLO! Questo esercizio è fondamentale soprattutto per la soluzione finale che verrà!

Iniziamo con il calcolo della parentesi, proprio come fatto prima.

8 \cdotp x+ 8 \cdotp 3 = 8x -24

8x+ 24 = 8x -24

Poi riordiniamo a destra e sinistra come sempre:

8x -8x = -24 -24

Sommiamo e notiamo che:

0x = -48

Questa è la forma classica che esce fuori, quando la soluzione è “impossibile”! Si ha soluzione impossibile in generale quando si ha:

0x = numero

Attenzione alle differenze con quando si ha la soluzione “indeterminata”. In quel caso, diverso, a destra anche si ha uno zero!

0x=0

Questa è invece indeterminata.

Facciamo altre equazioni terza media!

Esercizio 7. 3(2x +1 ) = 3 +6x


Anche questo esercizio è utile per consolidare la differenza fra indeterminata/impossibile. Partiamo con levare la parentesi:

3 \cdotp 2x + 3 \cdotp 1 = 3 +6x

6x + 3 = 3 +6x

Portiamo i termini al loro rispettivo posto:

6x -6x = 3 -3

Basta sommare per accorgersi che:

0x = 0

Questa era la forma che ci dava come soluzione…indeterminata! Non confondetevi con il caso di prima. Quando si ha ad entrambe le parti lo 0 allora la soluzione è indeterminata. Volete una ulteriore conferma di ciò? Provate a fare diviso 0 tutto:

x = \frac{0}{0}

E fatelo alla calcolatrice, vedete cosa esce fuori. Esce “error” perché non si può fare, al Liceo capirete il perché!

Esercizio 8. x- 3(x+1) = 5x - 4(x-1)


Da ora in poi le cose si complicano sempre più: ci sono ben due parentesi, con un segno meno davanti. Leggete con calma poiché ci sono dei passaggi da tenere a mente.

Studiamo il termine seguente e commentiamolo per capire come si fa la moltiplicazione:

-3(x+1)

Il 3 moltiplica ogni numero dentro la parentesi, ma anche il meno c’è! Dunque il risultato sarà:

-3x -3

Questo perché anche il “-” va ad attaccarsi ad ogni termine che sta nella parentesi tonda. L’altra parentesi è più difficile:

-4(x-1)

Facendo la moltiplicazione abbiamo due segni meno che si moltiplicano fra loro, ossia:

-4x -4 \cdotp -1

Ricordando che meno per meno fa più:

-4x +4

Quindi quando ci sono i segni meno, stiamo attenti! Procediamo ora a scrivere questi risultati nell’equazione dell’esercizio:

x- 3x -3 = 5x - 4x +4

Portiamo le x al primo membro:

x- 3x -3 -5x+4x= +4

Poi:

x- 3x -5x+4x= +4 +3

E addizioniamo:

-3x = 7

Dividiamo tutto per 3:

-x = \frac{7}{3}

E poi “cambiamo tutto di segno” (moltiplichiamo tutto per -1, passaggio che farà cambiare ad entrambi i membri il loro segno):

x = - \frac{7}{3}

Esercizio 9. 3x -5 +2(x-3) = 1 +5x


Questo esercizio porterà ad un risultato particolare, quindi fatelo! Fatelo prima voi e poi tornate qui, ci vediamo fra poco 🙂 E’ importante migliorare su questo aspetto. Pensate che in questo articolo viene sottolineato come la maggior parte degli studenti è carente in Matematica, ma seguendo le pagine del nostro sito tutto si risolve, ne siamo sicuri!

Focus su quella parentesi prima di tutto:

3x -5 +2x- 6 = 1 +5x

Poi il solito passaggio:

3x +2x-5x = 1 +5 +6

La solita somma:

0x = 12

Questa è la forma di una equazione di terza media che porta al risultato di “impossibile”!

Esercizio 10. 4 (x-3) -3(x-5) = 3(x+1)


Ben tre parentesi da fare qui, è facile sbagliare! Vediamo però se dopo 10 esercizi riuscite a non cadere nell’errore, dai provateci voi!

4x- 12 -3x +15 = 3x+3

Nulla di difficilissimo no? Siete allora pronti per i prossimi paragrafi, con più difficoltà crescenti!

4x -3x -3x= +3+12 -15

-2x= 0 \implies x = 0

Se questi esercizi sono troppo facili per voi, andate avanti, e se lo sono ancora potete andare sulla pagina delle equazioni per il Liceo! Lì potrebbero però comparire alcuni argomenti che non avete ancora visto.

Equazioni con frazioni (terza media)

Esercizio 1. \frac{1}{2} x -1 = 0


Iniziamo a prendere familiarità con le frazioni. Per saper fare le equazioni della terza media, con frazioni, serve conoscere:

• Massimo comune divisore
• Minimo comune multiplo
• Conoscenza del numeratore e del denominatore

Grazie alla conoscenza di questi 3 argomenti, siamo in grado di saper fare questi esercizi. Iniziamo. L’obiettivo primario non cambia, quindi portiamo il numero a destra:

\frac{1}{2} x = 1

A questo punto come facciamo a levare la frazione di mezzo? Abbiamo la nostra x sì, ma attaccata abbiamo \frac{1}{2} ! Grazie alla conoscenza del denominatore e del numeratore, sappiamo che moltiplicando per 2, la frazione si semplificherà!

2 \cdotp \frac{1}{2} x = 2 \cdotp 1

Il 2 sta sopra, all’altezza del numeratore, e poi c’è il 2 al denominatore. Segue che può essere effettuata la semplificazione:

x = 2

Fatto!

Esercizio 2. \frac{1}{2}x - 1 = \frac{1}{3} +2


Quando abbiamo più frazioni, il primo passaggio da fare è il minimo comune multiplo. Evitiamo di portare i termini da una parte all’altra all’inizio. Facciamo il minimo comune multiplo, prendendo come denominatore comune lo stesso ad entrambi i membri (in questo caso il Massimo Comune Divisore ci dice che dobbiamo prendere il 6):

\frac{3 \cdotp x - 6 \cdotp 1 }{6} = \frac{1 \cdotp 2 + 2 \cdotp 6 }{6}

Come vedete la tattica è prendere lo stesso denominatore comune ad entrambi i membri. Come mai? Lo capiremo fra pochissimo!

\frac{3x - 6 }{6} = \frac{2 + 12 }{6}

Adesso rispondiamo alla domanda: perché prendiamo lo stesso MCD a sinistra e destra? Perché in questo modo basterà moltiplicare tutto per 6 per levare le frazioni!

6 \cdotp \frac{3x - 6 }{6} = 6 \cdotp \frac{2 + 12 }{6}

3x - 6 = 2 + 12

Ed abbiamo, con questa strategia, tolto le frazioni. Ci siamo ricondotti alle equazioni classiche che abbiamo risolto all’inizio! Questa è facile e la sappiamo calcolare!

3x = 2 + 12 +6

3x = 20

Giungiamo alla soluzione:

x = \frac{20}{3}

Esercizio 3. \frac{2x+5}{3} - \frac{x+10}{6} = 0


Non facciamo nulla, se non il minimo comune multiplo! Facciamolo subito, senza primi altri passaggi:

\frac{2(2x+5) - (x+10) }{6} = 0

Se non avete capito questo passaggio, ve lo spieghiamo meglio. Partiamo dal fatto che dobbiamo fare l’mcm. Per la prima frazione dunque dobbiamo fare 6:3 e poi dobbiamo moltiplicare per 2x+5. Quindi verrà:

2 \cdotp (2x+5)

Le parentesi sono importanti quando al numeratore abbiamo più di un solo numero! Per la seconda frazione, abbiamo 6:6 per x+ 10. Ma attenzione! Davanti a quella frazione c’è un segno meno. Il segno meno va a moltiplicare tutto il numeratore! Torniamo all’equazione di terza media.

\frac{2(2x+5) - (x+10) }{6} = 0

Leviamo queste parentesi, svolgendo la moltiplicazione:

\frac{4x+20 - x-10}{6} = 0

A questo punto, proprio come prima, come si leva la frazione? Beh, moltiplicando tutto per 6!

6 \cdotp \frac{4x+20 - x-10}{6} = 6 \cdotp 0

4x+20 - x-10 = 0

Risolviamola facilmente:

4x - x = -20 + 10

3x = -10

Con il conseguente risultato:

x = - \frac{10}{3}

Esercizio 4. \frac{1}{3}x + \frac{1}{2}x = \frac{1}{4}x + \frac{1}{3}


Subito mcm! In questo caso calcolare il massimo comune divisore è già più difficile. Abbiamo un 3, poi un 2, poi un 4. L’MCD risultante è 12.

\frac{4x + 6x}{12} = \frac{ 3x + 4 }{12}

E poi come si levano queste frazioni? Ditemelo voi! Beh, sappiamo già:

4x + 6x = 3x + 4

4x + 6x -3x = + 4

Sommiamo:

7x = + 4

L’esercizio l’abbiam fatto!

x = \frac{ 4}{7}

Esercizio 5. \frac{ 5-3x }{4} + \frac{5}{3}x = \frac{3}{2} - \frac{ 3-5x }{3}


Senza pensarci nemmeno, mcm subito:

\frac{ 3(5-3x) + 20x }{12} = \frac{ 18- 4(3-5x) }{12}

Svolgiamo le moltiplicazioni corrispondenti:

\frac{ 15-9x + 20x }{12} = \frac{ 18- 12 + 20x }{12}

Se non avete capito ancora bene questa moltiplicazione con le parentesi, vedete assolutamente l’esercizio 9 e capirete tutto.

Leviamo i denominatori:

15-9x + 20x = 18- 12 + 20x

-9x + 20x -20x = 18- 12 -15

Senza che commentiamo questi passaggi, siete migliorati e siete diventati bravi adesso!

-9x = -9

x =1

Passiamo adesso ad esercizi davvero difficili, utilissimi per l’esame di terza media che verrà fra poco!

Equazioni difficili per esame di terza media

Esercizio 1. 2- \{2x -3 (2x-1) - 5[2x - (3x+1) +3 ]\} =0


Da ora, vi presentiamo alcune equazioni che potrebbero uscire all’esame di terza media, davvero difficili. In questo caso la difficoltà è presentata nella comparsa di ben tre parentesi diverse. Bisogna ricordarsi la seguente regoletta: prima levare le parentesi tonde, poi le quadre ed infine le graffe, in ordine.

Seguiamo questa regoletta, leviamo le tonde che vediamo:

2- \{2x -6x+3 - 5[2x -3x-1 +3 ]\} =0

Poi le quadre…

2- \{2x -6x+3 - 10x +15x +5 -15 \} =0

Ed infine la graffa, dove viene preceduta da un segno meno, dunque ne cambiamo il segno a tutti i numeri interni:

2- 2x +6x-3 + 10x -15x -5 +15 =0

A tal punto, chiamarla difficile non ha più senso! Risolvetela senza troppi fronzoli!

- 2x +6x + 10x -15x =-2 +5 +3 -15

- x = -9

Con il conseguente risultato:

x = 9

Esercizio 2. \frac{1}{4} (3x-2) + \frac{1}{3} (2x-1) = \frac{1}{4} (5x+6) + \frac{1}{3} (4x+5)


Qui la difficoltà principale risulta nella moltiplicazione dei termini dentro la parentesi con una frazione, come si fa? La logica è proprio la stessa. Vediamo la prima parentesi per fare un esempio e vedere come si agisce. Facciamo la moltiplicazione, scrivendo esplicitamente:

\frac{1}{4} (3x-2) \implies \frac{1}{4} \cdotp 3x- \frac{1}{4} \cdotp 2

Il “3x” sta all’altezza del numeratore, quindi lo possiamo mettere sopra; stesso col 2.

\implies \frac{3x}{4} - \frac{2}{4}

Ed abbiamo fatto. L’unica cosa aggiuntiva è la semplificazione alla seconda frazione, ovviamente per 2:

\implies \frac{3x}{4} - \frac{1}{2}

E questo è ciò che faremo per ogni moltiplicazione. Ne risulta:

\frac{3x}{4} - \frac{1}{2} + \frac{2x}{3} -\frac{1}{3} = \frac{5x}{4} + \frac{6}{4} + \frac{4x}{3} +\frac{5}{3}

A questo punto facciamo un bel minimo comune multiplo GIGANTESCO! Tanti numeri da scrivere, ricontrolliamo sempre.

\frac{ 9x - 6 + 8x - 4 }{12} = \frac{ 15x + 18 + 16x + 20 }{12}

E’ facile sbagliare, però se il procedimento è giusto non preoccupatevi, vi metteranno lo stesso un buon voto. Moltiplichiamo per 12 tutto:

9x - 6 + 8x - 4 = 15x + 18 + 16x + 20

9x + 8x -15x - 16x = + 18 + 20 +6+4

Sommiamo i termini simili.

-14x = 48 \implies x = - \frac{48}{14}

E se desiderate, andate pure a semplificare la frazione, noi ci scocciamo adesso 🙂

Comunque, questa pagina sulle equazioni terza media, per la verifica in classe e per l’esame, è finita qui. Speriamo non ci siano stati errori. Nel caso di forti dubbi, non esitate a contattarci alla nostra email! Vi risponderemo e vi spiegheremo i passaggi privatamente per email e gratis!