MASSIMI e MINIMI: 20 esercizi SVOLTI !

MASSIMI e MINIMI: 20 esercizi SVOLTI ! La ricerca dei massimi e minimi e punti non derivabili è uno dei punti finali dello studio di una funzione: argomento d’esame e di verifica in classe, quindi molto importante! Prima di esercitarvi su questo argomento, bisogna saper fare assolutamente le derivate ed il dominio. In questa pagina vedremo come calcolare massimi e minimi, flesso orizzontale e cosa succede se un punto non è derivabile. Iniziamo subito con l’indice!

Indice

• Massimi e minimi: esercizi
• Esercizi sul Flesso orizzontale
• Esempi Punti di non derivabilità
• Consigli generali

Iniziamo subito con massimi e minimi: esercizi svolti !

Massimi e minimi: esercizi

Funzioni generali

Esercizio 1. $y=x^3 -3x^2 +1$


E’ sempre utile partire dal dominio: in questo caso funzione polinomiale e quindi:

$x \in \Reals$

Per trovare i massimi e i minimi di una funzione si fa la derivata della funzione y e la si pone >0.

Quindi iniziamo a calcolare la derivata della funzione y:

$y'=3x^2 -6x$

E poniamo y’>0.

$3x^2 -6x >0$

Mettiamo in evidenza la x.

$x(3x -6) >0$

Risolviamo questa disequazione con un falso sistema.

$\big\| x>0 \\ \big\| 3x-6>0$

$\big\| x>0 \\ \big\| x>2$

Studiamo ora i segni.

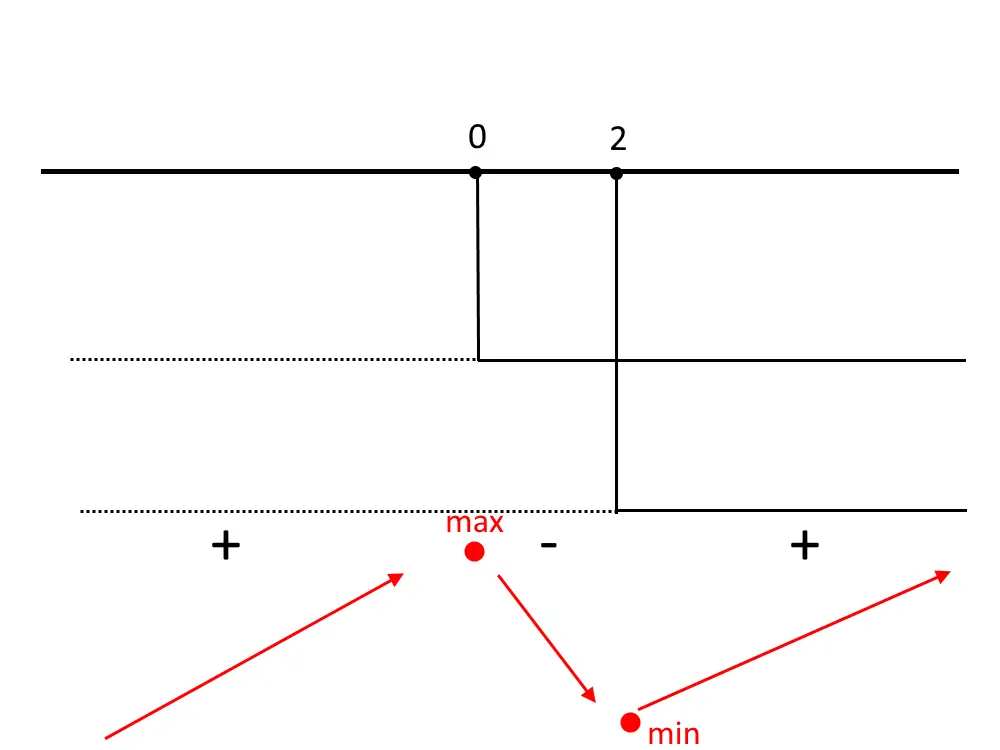
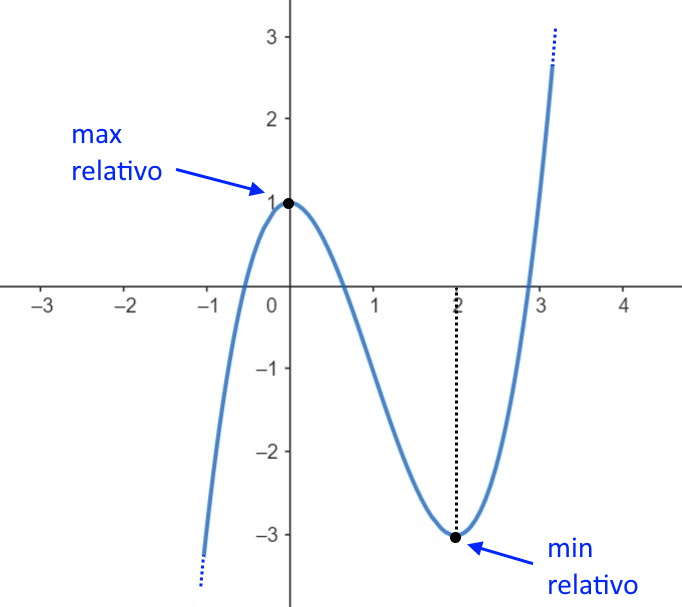
Negli intervalli in cui abbiamo un segno positivo + disegniamo che la funzione è crescente, mentre negli intervalli in cui abbiamo un segno negativo – la funzione è decrescente. Quando la funzione cresce e poi decresce allora quello è un punto di massimo relativo, quando la funzione decresce e poi cresce allora esso è un punto di minimo relativo.

Quindi vedendo lo schemino, capiamo che:

x=0 massimo, x=2 minimo.

Esercizio 2. $y=\frac{1}{2} e^{-x^2}$


Anche qui abbiamo un esponenziale e quindi il dominio è:

$x \in \Reals$

Passiamo a calcolare i massimi e minimi della funzione. Calcoliamo la derivata della funzione y.

$y'=-2x \cdotp \frac{1}{2} e^{-x^2} = - x e^{-x^2}$

E poi poniamo y’>0.

$- x e^{-x^2} >0$

Essendo che l’esponenziale è sempre positivo, allora per essere il tutto >0 significa che:

-x>0 ossia che x<0.

Disegniamo i segni di questa condizione.

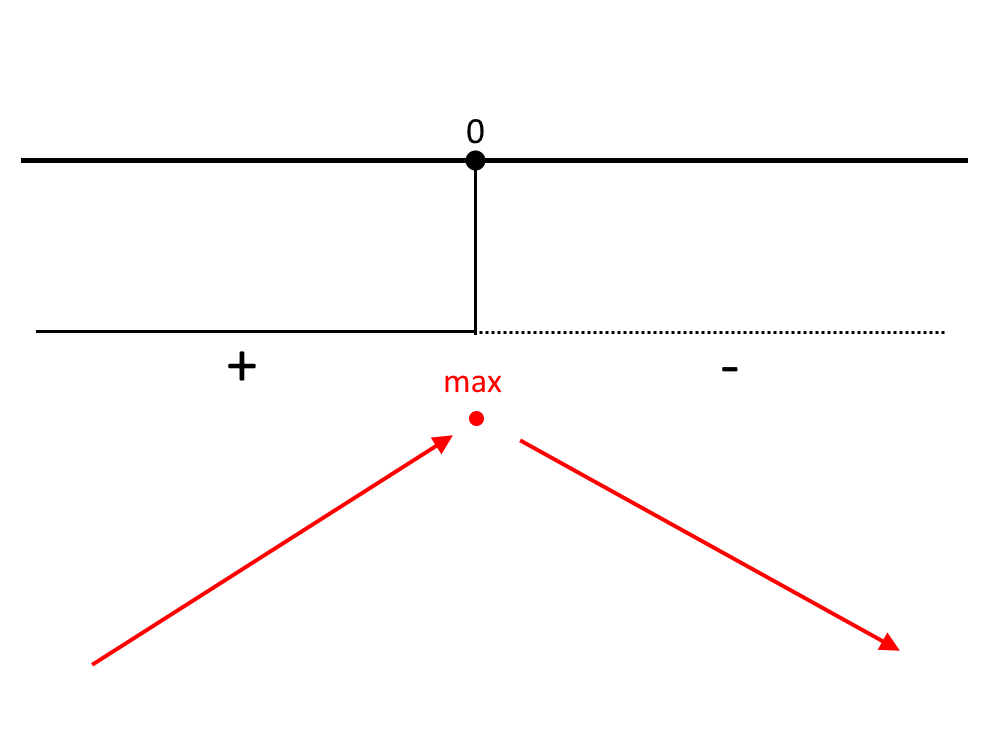
Esercizio 3. $y=\frac{2x^2}{x-1}$


Calcoliamo il dominio della funzione per prima cosa, perchè a volte come vedremo ciò si rivelerà utile.

D:$x-1 \ne 0 \implies x \ne 1$

Ora calcoliamo la derivata di y.

$y'=\frac{4x(x-1) - 2x^2}{(x-1)^2}$

$y'=\frac{2x^2 -4x}{(x-1)^2} =\frac{2x(x -2)}{(x-1)^2}$

E poi poniamo come sempre y’>0, come vedete è sempre lo stesso procedimento.

$\frac{2x(x -2)}{(x-1)^2}>0$

Risolviamo il falso sistema.

$\big\| 2x(x -2) >0 \\ \big\| (x-1)^2>0$

Il secondo è sempre positivo e basta che $x\ne 1$ e ciò lo abbiamo già nel dominio della funzione.
Il primo termine lo risolviamo con un altro falso sistema.

$\big\| 2x >0 \\ \big\| x-2>0$

$\big\| x >0 \\ \big\| x>2$

E prendiamo la parte positiva, con intervalli +.

$x<0 \land x>2$

E mettiamo questo nel falso sistema della derivata.

$\big\| x<0 \land x>2 \\ \big\| \forall x\ne 1$

Studiamo i segni, e notiamo che:

x=0 massimo, x=2 minimo.

Continuiamo con massimi e minimi: esercizi svolti !

Esercizio 4. $y=\frac{-2}{\sqrt{x^2 +4}}$


Studiamo prima il dominio, della radice e della frazione. Iniziamo dal dominio della radice:

$\sqrt{x^2 +4 } \ge 0 \implies \forall x$

E’ sempre positivo o uguale a zero perchè abbiamo un quadrato di x sommato ad un numero positivo.
Poi passiamo al dominio della frazione:

$x^2 +4 \ne 0 \implies x^2 \ne -4$

Ed anche questo è sempre diverso da -4, essendo x^2 positivo.

Quindi D:$x \in \Reals$

Passiamo finalmente a trovare massimi e minimi, facciamo la derivata.

$y'=\frac{2 \cdotp \frac{2x}{2\sqrt{x^2 +4 }} }{x^2 +4}= \frac{ \frac{2x}{\sqrt{x^2 +4 }} }{x^2 +4}$

$= \frac{2x}{\sqrt{x^2 +4 }} \frac{1}{ x^2 +4 } = \frac{2x}{(x^2 +4 )^{\frac{3}{2} } }$

$= 2x (x^2 +4 )^{-\frac{3}{2}}$

E poniamo questa quantità maggiore di zero.

$2x (x^2 +4 )^{-\frac{3}{2}} >0$

Con un falso sistema lo possiamo risolvere.

$\big\| 2x >0 \\ \big\| (x^2 +4 )^{-\frac{3}{2}} >0$

Il secondo è sempre positivo.

$\big\| x >0 \\ \big\| \forall x$

Disegniamo i segni. E ricaviamo che:

x=0 minimo.

Esercizio 5. $y=\sqrt{\frac{1}{x^2 +1}}$


Prima cosa…ditela voi…dominio, esatto! Abbiamo qui una funzione radice ed una fratta. Partiamo dalla radice che è immediato il dominio in questo caso.

$\frac{1}{x^2 +1} \ge 0$

Il numeratore è positivo, il denominatore è 1 sommato con un quadrato, quindi anch’esso positivo. L’argomento della radice è sicuramente positivo per ogni x.

Per la frazione denominatore diverso da zero:

$x^2 +1 \ne 0 \implies x^2 \ne -1$

Ma questo avviene sempre, perchè esso è positivo o uguale a zero, e quindi sempre diverso da -1. Quindi il dominio è:

D: $x \in \Reals$

Ora possiamo fare la derivata di y: non è semplicissima, quindi per non sbagliare partiamo sempre dalla funzione più esterna e poi facciamo la derivata via via di quella più interna. Quindi si parte con la derivata della radice, a cui poi si moltiplica la derivata della frazione.

$y'=\frac{1}{2 \sqrt{\frac{1}{x^2 +1}}} \cdotp \frac{-2x}{(x^2 +1)^2}$

Semplifichiamo il 2 e poi scriviamo la radice nel modo seguente:

$=\frac{1}{ \frac{1}{\sqrt{x^2 +1}}} \cdotp \frac{-x}{(x^2 +1)^2}$

Poi portiamo il denominatore al numeratore, eliminando quindi la frazione di frazione:

$= \frac{-x \sqrt{x^2 +1}}{(x^2 +1)^2}$

Per la proprietà della potenza:

$\frac{a^b}{a^c} = a^{b-c}$

Scriviamo quindi:

$= -x (x^2 +1 )^{-\frac{3}{2}}= -x \frac{1}{\sqrt{(x^2+1)^3}}$

Tutto questo casino è stato per mettere in maniera ordinata la derivata e quindi fare il prossimo passaggio in maniera semplice. E’ importantissimo non complicarsi la vita anche con esercizi non così difficili!

Di fatti ora y’>0 sarà un gioco da ragazzi.

$-x \frac{1}{\sqrt{(x^2+1)^3}} >0$

Il secondo termine è sempre positivo. Il primo invece no, quindi basta che sia positivo anche il primo termine, quindi:

-x>0 e quindi x<0 semplicemente, e disegnando i segni, allora notiamo facilmente che:

x=0 massimo.

Esercizio 6. $y=\frac{\ln x}{x}$


Abbiamo due funzioni: logaritmo e frazione. Il dominio è semplice qui, per il logaritmo abbiamo che x>0, mentre per la frazione
$x \ne 0$, e quindi il dominio è:

D: x>0

Calcoliamo la derivata adesso.

$y'=\frac{\frac{1}{x} x - \ln x}{x^2} =\frac{1 - \ln x}{x^2}$

Ora calcoliamo y’>0.

$\frac{1 - \ln x}{x^2} >0$

Con un falso sistema.

$\big\| 1 - \ln x>0 \\ \big\| x^2 > 0$

Ovviamente x^2 è sempre positivo per ogni x tranne per x=0. (Il dominio lo mettiamo alla fine).

$\big\| \ln x<1 \\ \big\| \forall x \ne 0$

$\big\| x<e \\ \big\| \forall x \ne 0$

Facciamo il grafico dei segni, e ricaviamo che

x=e massimo, nel dominio x>0. Quindi tutto ciò che sta prima non lo consideriamo nella tabella dei segni chiaramente.

Esercizio 7. $y=18 \ln x - \frac{3}{4} x^2$


Per quanto riguarda il dominio, dobbiamo solo considerare il dominio e quindi
D: x>0.

Facciamo la derivata della funzione.

$y'=18 \frac{1}{x} - \frac{3}{4} 2x =18 \frac{1}{x} - \frac{3}{2} x$

$=\frac{36- 3x^2}{2x}$

E poi come sempre poniamo y’>0.

$\frac{36- 3x^2}{2x} >0$

Lo svolgiamo con un falso sistema.

$\big\| 36- 3x^2 >0 \\ \big\| 2x >0$

$\big\| x^2 < 12 \\ \big\| x >0$

Per il primo andiamo a prendere valori interni, essendoci un minore.

$\big\| -2\sqrt{3} < x < 2\sqrt{3} \\ \big\| x >0$

Dallo studio dei segni notiamo che, considerando solamente x>0 che è il dominio, abbiamo solamente il punto:

di massimo relativo $x=2 \sqrt{3}$

Continuiamo con massimi e minimi: esercizi svolti !

Esercizi sul Flesso orizzontale

Esercizio 8. $y=\frac{x^3}{x-3}$


Partiamo dal dominio, che è davvero immediato qui, visto che dobbiamo solo porre il denominatore diverso da zero.

D:$x-3 \ne 0 \implies x \ne 3$

Ora passiamo al calcolo della derivata della funzione.

$y'=\frac{3x^2 (x-3) -x^3}{(x-3)^2} = \frac{3x^3 -9x^2 -x^3 }{(x-3)^2}=$

$= \frac{2x^3 -9x^2 }{(x-3)^2} =\frac{x^2 (2x-9)}{(x-3)^2}$

Adesso possiamo porre y’>0.

$\frac{x^2 (2x-9)}{(x-3)^2} >0$

Lo risolviamo con un falso sistema.

$\big\| x^2 (2x-9)>0 \\ \big\| (x-3)^2>0$

Il secondo termine è sempre positivo tranne in x=3 per la quale è zero.
Per quanto riguarda il membro facciamo un altro falso sistema molto veloce, ovviamente non serve, però per chi non è pratico è meglio farlo.

$\big\| x^2>0 \\ \big\| (2x-9)>0$

$\big\| \forall x \ne 0 \\ \big\| x> \frac{9}{2}$

Da cui ricaviamo semplicemente l’intervallo positivo $x> \frac{9}{2} \land x \ne 0$ e anche la condizione di x diverso da zero.

Sostituiamo nel primo falso sistema.

$\big\| x> \frac{9}{2} \land x \ne 0 \\ \big\| \forall x \ne 3$

Notiamo che $x=\frac{9}{2}$ è un punto di minimo. Ed inoltre ricaviamo un grafico dei segni particolare, perchè come potete vedere nel punto x=3 c’è un punto di discontinuità essendo il dominio, quindi la funzione non esiste lì. Mentre in x=0 la funzione esiste, e notiamo che decresce e poi decresce ancora, e quando abbiamo una situazione di questo tipo allora x=0 è un punto di flesso orizzontale, ossia la funzione fa così:

E’ importantissimo non confondere un punto di discontinuità che non può essere un punto di flesso orizzontale, perchè la funzione non esiste lì. Mentre un punto di flesso orizzontale è un punto tale che la funzione esiste. Ed inoltre la funzione o cresce/cresce o decresce/decresce.

Fate anche il prossimo esercizio per capire meglio!

Continuiamo con altri massimi e minimi: esercizi svolti!

Esercizio 9. $y=\frac{x^3}{3} -x^2 +x$


Il dominio è D:$x \in \Reals$ quindi la funzione è sempre definita e continua, non ha buchi.

Adesso troviamo la derivata.

$y'=3\frac{x^2}{3} -2x +1 =x^2 -2x +1$

Possiamo renderlo una forma più semplice, trovando il delta/quarti.

$\frac{\Delta}{4}= 1-1=0$

Adesso troviamone le due soluzioni uguali:

$x_{1,2} = 1$

E quindi possiamo scrivere

$y=x^2 -2x +1 =(x-1)^2$

Poniamo derivata y’>0.

$(x-1)^2 >0$

Qua come possiamo vedere abbiamo che essa è sempre maggiore di zero tranne per x=1:

$\forall x \ne 1$

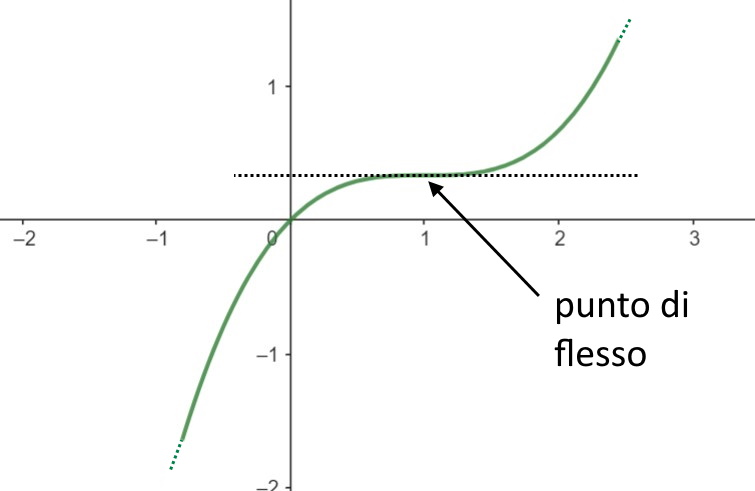
E quindi il grafico dei segni ci porta alla seguente figura.

Quindi x=1 è un punto di flesso orizzontale, perchè la funzione esiste lì.

Esercizio 10. $y=\frac{1}{5}x^5 + \frac{1}{3}x^3$


Il dominio è chiaramente $x \in \Reals$ quindi la funzione è sempre continua.

Ora la derivata!

$y'=\frac{1}{5}5x^4 + \frac{1}{3}3x^2 =x^4 + x^2$

Poniamo y’>0.

$x^4 + x^2 >0$

E senza fare nessun calcolo capiamo bene che la somma di un quadrato ed una x alla quarta sono entrambi sempre positivi, ma fanno zero nel caso in cui x=0. Quindi ricaviamo che esso è maggiore di zero:

$\forall x \ne 0$

E quindi disegnando il grafico dei segni, la funzione cresce/cresce, e nel punto x=0 abbiamo un flesso orizzontale.

Esercizio 11. $y=\frac{x^2 -1}{2x-2}$


Calcoliamo come sempre prima il dominio, denominatore diverso da zero:

$2x-2 \ne 0 \implies x \ne 1$

Ora, prima di calcolare la derivata, possiamo semplificare la forma della funzione stessa. Leggete sempre per un paio di minuti la traccia prima di iniziare a scrivere!

$y=\frac{x^2 -1}{2x-2}=\frac{(x-1)(x+1)}{2(x-1)}=\frac{x+1}{2}$

Se ora vi state chiedendo perchè non abbiamo semplificato all’inizio, beh il dominio lo si deve calcolare sulla funzione che ci viene data, e poi solo dopo si può mettere mano.

Calcoliamo la derivata adesso.

$y'=\frac{1}{2}$

Poniamo y’>0.

$\frac{1}{2} >0$

E questo è sempre per ogni x maggiore di zero.

Quindi la funzione è crescente e basta. Non ci sono punti di minimo o massimo, e non ci sono punti di flesso orizzontale! Perchè x=1 è un punto di discontinuità, quindi non può esserci un punto di flesso!
Ricordatevi che la funzione deve esistere per essere un punto di flesso!


Continuiamo con massimi e minimi: esercizi svolti !

Flessi in funzioni goniometriche

Esercizio 12. $y=4 \cos^2 x +4 \cos x -1$ in $[0, \pi ]$



Innanzitutto la funzione è definita su tutto l’intervallo che l’esercizio ci ha dato, perchè il coseno non ha problemi di dominio. Passiamo quindi al calcolo della derivata prima di questa funzione di soli coseni.

$y'=-8 \cos x \sin x - 4 \sin x$

Ora possiamo passare al calcolo della y’>0:

$-8 \cos x \sin x - 4 \sin x >0$

Per la risoluzione, metto in evidenza il seno.

$\sin x (-8 \cos x- 4) >0$

E lo risolviamo con un falso sistema.

$\big\| \sin x > 0 \\ \big\| -8 \cos x- 4 >0$

$\big\| \sin x > 0 \\ \big\| \cos x < -\frac{1}{2}$

Vediamo per quali intervalli di angoli sono vere queste relazioni, disegnando una circonferenza goniometrica; inoltre ricordiamoci che il problema ci ha detto che siamo nell’intervallo $[0, \pi ]$. Troviamo:

$\big\| 0<x<\pi \\ \big\| \frac{2}{3} \pi < x < \pi$

Dove ricordiamoci che gli estremi di un intervallo derivato non vanno presi. Disegniamo quindi su uno schema di segni questo falso sistema, e prendiamo gli intervalli positivi. Abbiamo 3 punti di massimo e minimo perchè vanno presi ovviamente anche gli estremi:

x=0 punto di massimo insieme a $x=\pi$;

$x=\frac{2}{3} \pi$ punto di minimo.

Continuiamo con massimi e minimi: esercizi svolti !

Esempi Punti di non derivabilità

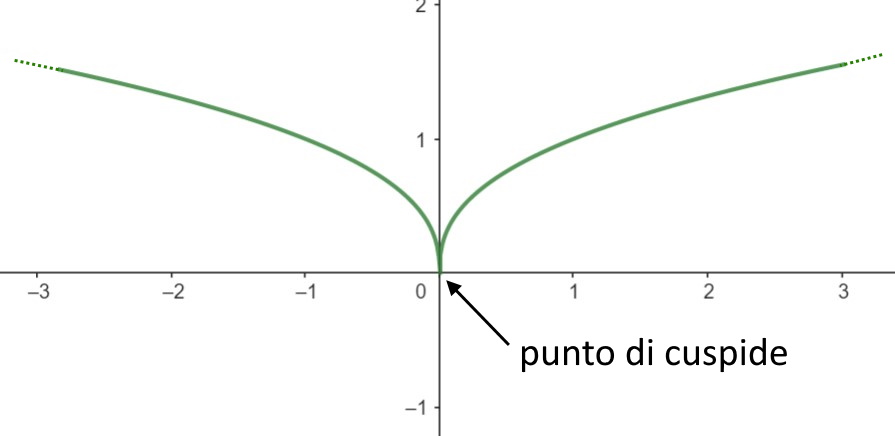
Cuspide

Quando c’è un punto $x_0$ di non derivabilità, ossia un punto non derivabile ma che appartiene al dominio della funzione: esso è un punto di cuspide, se:

$\lim\limits_{x \to x_0^{\pm} } f'(x) = \pm \infin$

E l’importante è che i due infiniti devono essere di segno opposto.

Esercizio 16. $y=\sqrt[5]{x^2}$


Come possiamo vedere la funzione è definita per ogni x, essendo l’esponente della radice dispari.

D:$x \in \Reals$

Mentre se calcoliamo la derivata:

$y'=\frac{2}{5} x^{-\frac{3}{5} } = -\frac{2}{5 \sqrt[5]{x^3}}$

E come possiamo vedere il dominio della derivata implica che:

$x \ne 0$

che è un punto di non derivabilità, ma che appartiene comunque al dominio della funzione y.

Calcoliamo adesso i due limiti destro e sinistro del punto:

$\lim\limits_{x \to 0^+ } -\frac{2}{5 \sqrt[5]{x^3}} = -\frac{2}{5 \sqrt[5]{0^+}}= - \infin$

$\lim\limits_{x \to 0^- } -\frac{2}{5 \sqrt[5]{x^3}} = -\frac{2}{5 \sqrt[5]{0^-}}= + \infin$

E quindi deduciamo che è un punto di cuspide, di fatti la funzione in tale punto forma una cuspide.

Esercizio 17. $y=\sqrt[3]{(x-1)^2}$


Essendo l’esponente della radice dispari, la funzione è definita su tutto R.

D:$x \in \Reals$

Adesso calcoliamo y’.

$y'=\frac{2}{3}(x-1)^{-\frac{1}{3}} =\frac{2}{3\sqrt[3]{x-1}}$

La derivata è definita per ogni x tranne con denominatore diverso da zero, quindi vi è un punto di non derivabilità in:

$x \ne 1$

Calcoliamo i limiti per vedere se si tratta di una cuspide.

$\lim\limits_{x \to 1^+ } \frac{2}{3\sqrt[3]{x-1}} = \frac{2}{3\sqrt[3]{1^+ -1}}=\frac{2}{3\sqrt[3]{0^+}}= + \infin$

$\lim\limits_{x \to 1^- } \frac{2}{3\sqrt[3]{x-1}} = \frac{2}{3\sqrt[3]{1^- -1}}=\frac{2}{3\sqrt[3]{0^-}} = - \infin$

E quindi x=1 è un punto di cuspide.

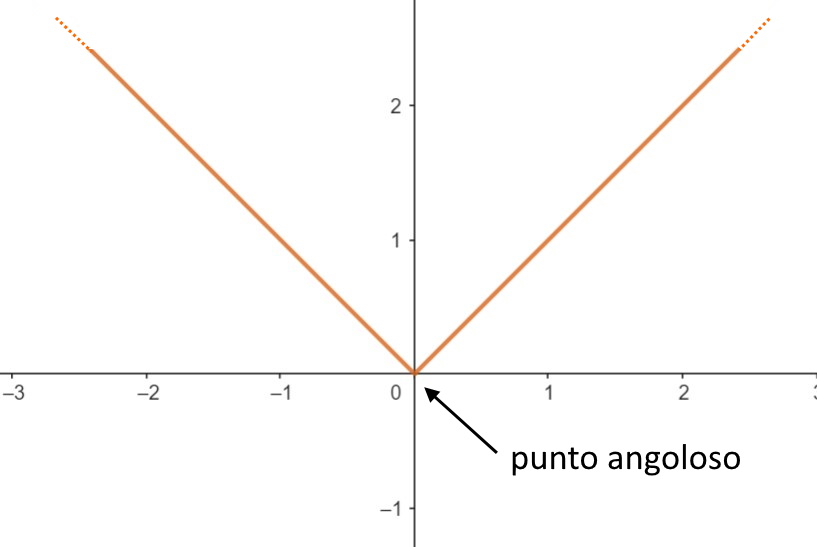
Punto Angoloso

Un punto angoloso $x_0$ è un punto di non derivabilità ma che appartiene al dominio della funzione, in cui:

$\lim\limits_{x \to x_0^+ } f'(x) = h$

$\lim\limits_{x \to x_0^- } f'(x) = g$

In cui $h \ne g$. Quindi i limiti devono essere diversi. Chiaramente non rientra il caso in cui uno è – infinito e l’altro è + infinito, altrimenti si parlerebbe di cuspide.

Basta che siano diversi, uno può anche essere infinito, per esempio:

$h=2, g=+ \infin$

Esercizio 18. $y=|x|$


Famosissima funzione nota per il punto angoloso è il valore assoluto di x. Essa è definita in tutto R.

D:$x \in \Reals$

Quando abbiamo un valore assoluto, lo scomponiamo sempre come segue:

$y= \begin{cases} -x &\text{se } x<0 \\ x &\text{se } x\ge 0 \end{cases}$

Ora possiamo calcolare la derivata y’.

$y'= \begin{cases} -1 &\text{se } x<0 \\ 1 &\text{se } x> 0 \end{cases}$

Ricordatevi che la derivata “elimina” gli estremi del dominio, perciò x=0 non si prende. x=0 è un punto di non derivabilità.

Calcoliamo i due limiti adesso:

$\lim\limits_{x \to 0^+ } 1 = 1$

$\lim\limits_{x \to 0^- } -1 = -1$

Che sono diversi, e quindi x=0 è un punto angoloso.

Esercizio 19. $y=|2 \ln x | -3$


Abbiamo un logaritmo, per cui il dominio è x>0.

Scriviamo la funzione come sempre quando ci sono i valori assoluti come segue:

$y= \begin{cases} 2\ln x -3 &\text{se } x \ge 1 \\ -2\ln x -3 &\text{se } 0<x<1 \end{cases}$

Se non vi ricordate questa scrittura: dovete pensare che la funzione dentro al logaritmo deve essere sempre positiva o uguale a zero. Nel primo caso:

$2 \ln x \ge 0 \implies x \ge e^0 = 1$

$2 \ln x < 0 \implies 0<x<1$

Lo zero perchè ricordatevi che il dominio è x>0.

Comunque ritorniamo all’esercizio, calcoliamo adesso la derivata.

$y'= \begin{cases} 2\frac{1}{x} &\text{se } x > 1 \\ -2\frac{1}{x} &\text{se } 0<x<1 \end{cases}$

x=1 non è più compreso, esso ora è un punto di non derivabilità.

Per cui calcoliamo i limiti e vediamo che tipo di punto è.

$\lim\limits_{x \to 1^+ } 2\frac{1}{x} = 2$

$\lim\limits_{x \to 1^- } -2\frac{1}{x} = -2$

I due limiti sono diversi, e quindi si tratta di un punto angoloso.

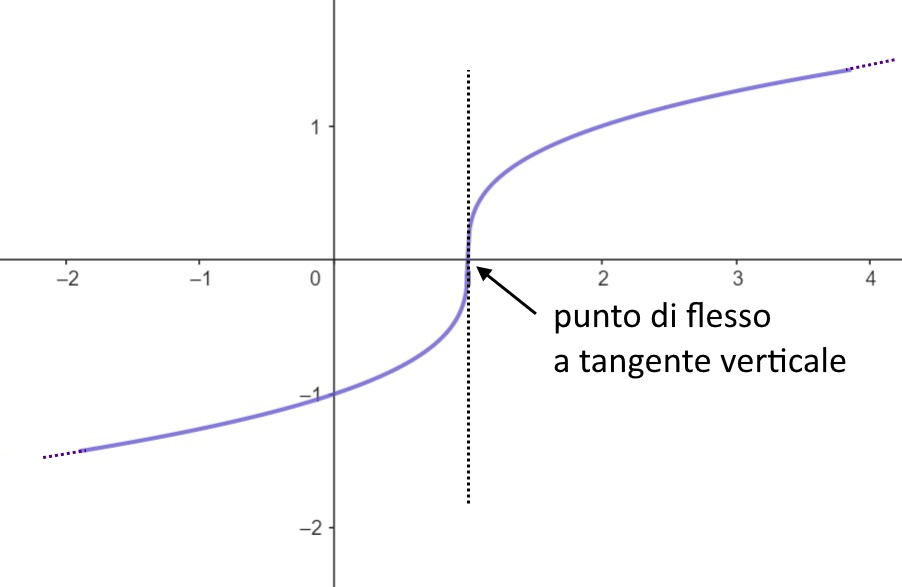
Flesso a tangente verticale

Un punto di non derivabilità $x_0$ ma che appartiene al dominio della funzione, è detto punto di flesso a tangente verticale se:

$\lim\limits_{x \to x_0^+ } f '(x) = \pm \infin$

$\lim\limits_{x \to x_0^- } f '(x)= \pm \infin$

L’importante qui è che entrambi siano uguali! Cioè entrambi – infinito o entrambi + infinito.

Esercizio 20. $y=\sqrt[3]{x-1}$


Essendo esponente dispari, il dominio è tutto R e non ci sono restrizioni.

D:$x \in \Reals$

Calcoliamo la derivata della funzione dell’esercizio.

$y'=\frac{1}{3} (x-1)^{-\frac{2}{3} } =\frac{1}{3\sqrt[3]{(x-1)^2}}$

E questa è definita per ogni $x \ne 1$

Quindi x=1 è un punto di non derivabilità. Calcoliamo i limiti destro e sinistro e vediamo cosa succede:

$\lim\limits_{x \to 1^+ } \frac{1}{3\sqrt[3]{(x-1)^2}} =\frac{1}{3\sqrt[3]{(1^+-1)^2}}=$

$=\frac{1}{3\sqrt[3]{(0^+)^2}}= + \infin$

$\lim\limits_{x \to 1^- } \frac{1}{3\sqrt[3]{(x-1)^2}} =\frac{1}{3\sqrt[3]{(1^- -1)^2}}=$

$=\frac{1}{3\sqrt[3]{(0^-)^2}}= \frac{1}{3\sqrt[3]{0^+}} = + \infin$

I due limiti sono entrambi + infinito, e quindi si tratta di un punto di flesso a tangente verticale.

---

Consigli generali

---

Siamo riusciti a fare ben 20 esercizi svolti sui massimi e minimi! Il prossimo step sarà lo studio della concavità di una funzione.
Continuate a studiare con altri esercizi svolti sul nostro sito, di matematica che altro ancora!


Per approfondire: https://it.wikipedia.org/wiki/Massimo_e_minimo_di_una_funzione

Asintoti
funzione
esercizi

Concavità
funzioni
esercizi