Studio Concavità delle funzioni
Studio Concavità funzioni: ESERCIZI SVOLTI! L’ultimo passo per completare lo studio di una funzione è studiarne la concavità! Non è difficile, quindi potete stare tranquilli! Prima di addentrarci in questi esercizi svolti, vi consiglio prima vedere come si calcola il dominio di una funzione e come trovare i massimi e minimi di una funzione…quindi saper fare le derivate! Fatto ciò possiamo iniziare! Faremo ben 15 esercizi. Partiamo con l’indice.
Indice
Iniziamo subito a vedere degli esercizi svolti sullo studio delle concavità di una funzione generica: polinomiale, fratta, esponenziale, logaritmica ecc.
Calcolo concavità: funzioni generali
In questi esercizi sarà indispensabile calcolarne prima il dominio, altrimenti non si può studiarne la concavità! Quindi se non sapete i domini delle funzioni, fate una cosa per volta! Vedremo inoltre solamente il calcolo delle concavità e della derivata seconda, quindi se non sapete come si calcolano le derivate, cliccateci sopra ed esercitatevi su una cosa alla volta.
A differenza dei massimi e minimi e quindi della derivata prima, lo studio delle concavità non presenta molte difficoltà o cose particolari nei punti di non derivabilità ecc., quindi sono molto più semplici!
Esercizio 1. y=\frac{x-3}{(x+1)^3}
Calcoliamo come sempre prima il dominio, perchè dobbiamo capire in quali intervalli la funzione esiste e quindi dove possiamo calcolare le concavità.
Qui abbiamo solo una funzione fratta, quindi essa è definita per ogni x tranne per denominatore diverso da zero:
D: (x+1)^3 \ne 0 \implies x \ne -1
La funzione è definita in tutto R tranne per x=-1.
Calcolare la concavità significa studiare il segno della derivata seconda. Quindi iniziamo a calcolare la derivata prima della funzione.
y'=\frac{(x+1)^3 - 3(x-3)(x+1)^2}{(x+1)^6}
Mettiamo in evidenza, e poi semplifichiamo.
y'=\frac{(x+1)^2 [(x+1) - 3(x-3)]}{(x+1)^6} = \frac{ (x+1) - 3(x-3)}{(x+1)^4} =
Ricordate che prima di iniziare a fare calcoli, bisogna trovare il modo migliore per semplificare la forma della derivata in questo caso, dobbiamo semplificarci la vita!
y'= \frac{ 10-2x }{(x+1)^4}
Ora il nostro obiettivo non sono i massimi e minimi. Quindi calcoliamo la derivata seconda e vi facciamo vedere come trovare le varie concavità.
y''= \frac{ -2(x+1)^4 -4(10-2x)(x+1)^3 }{(x+1)^8}
Mettiamo in evidenza come prima, e poi semplifichiamo.
y''= \frac{ (x+1)^3 [-2(x+1) -4(10-2x)] }{(x+1)^8} = \frac{ -2(x+1) -4(10-2x) }{(x+1)^5}
y''= \frac{ 6x -42 }{(x+1)^5}
Calcolare la derivata seconda significa fare tanti calcoli, quindi fate attenzione che è facile sbagliare!
A questo punto poniamo y”>0 e ne studiamo il segno.
\frac{ 6x -42 }{(x+1)^5} >0
Essendo una disequazione fratta, la risolviamo con un falso sistema.
\big\| 6x -42 > 0 \\ \big\| (x+1)^5 > 0
\big\| 6x > 42 \\ \big\| x+1 > 0
\big\| x > 7 \\ \big\| x > -1
Facciamo lo schema dei segni: gli intervalli con il + hanno la concavità verso l’alto (faccina felice), gli intervalli con il – hanno la concavità verso il basso (faccina triste), come segue.
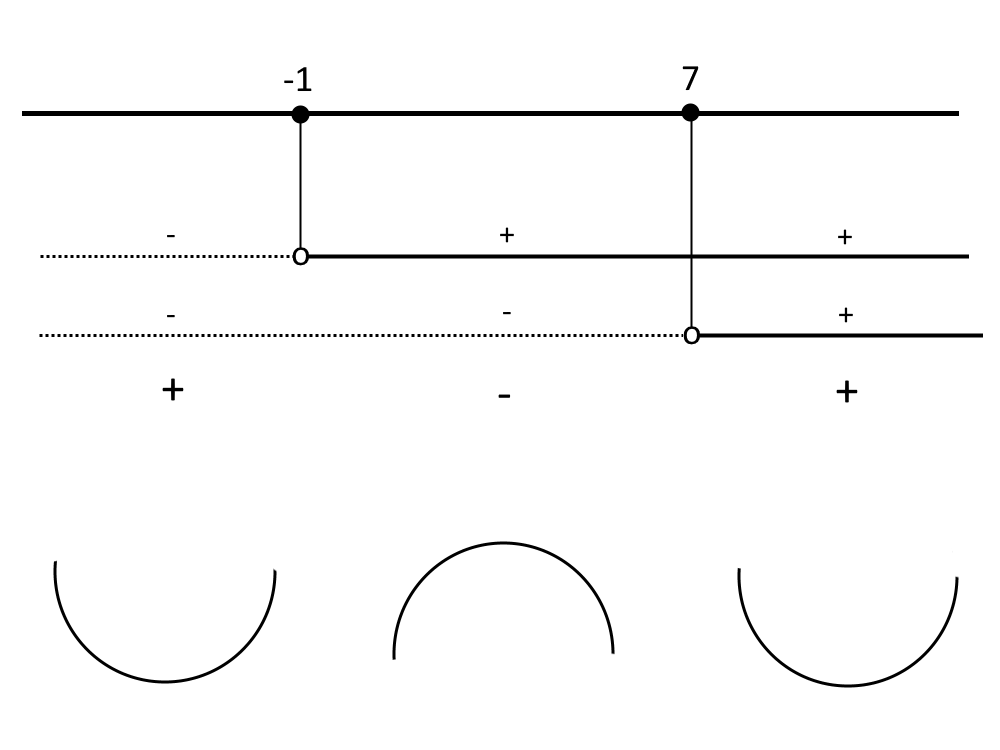
(ricordatevi sempre di tenere conto del dominio in questo disegno, cioè in questo caso il -1 non bisogna prenderlo)
Esercizio 2. y=2 \ln x + \frac{1}{x}
Come sempre, prima di ogni cosa dominio! Qui abbiamo una funzione logaritmica e una fratta. Scriviamo in un sistema ogni singolo dominio, e poi prendiamo i valori comuni e cerchiamo di scrivere un unico comune dominio:
D: \begin{cases} x>0 \\ x \ne 0 \end{cases}
Quindi D:x>0
Adesso passiamo al calcolo della derivata prima e poi della derivata seconda.
y'=2 \frac{1}{x} - \frac{1}{x^2} = \frac{2x - 1}{x^2}
Calcoliamo ora y”:
y''= \frac{2x^2 -2(2x-1)x}{x^4}
Attenzione sempre con la derivata seconda che sono a volte tanti calcoli ed è facile sbagliare!
y''= \frac{-2x^2 +2x}{x^4} = \frac{2x(-x+1)}{x^4} = \frac{2(-x+1)}{x^3}
Adesso che la forma è bella compatta e semplice studiamone il segno: y”>0.
\frac{2(-x+1)}{x^3} >0
\big\| 2(-x+1) > 0 \\ \big\| x^3 > 0
\big\| -x+1 > 0 \\ \big\| x > 0
\big\| x<1 \\ \big\| x > 0
Vedendo lo schema dei segni, e considerando solamente l’intervallo x>0 che è il dominio! Abbiamo che:
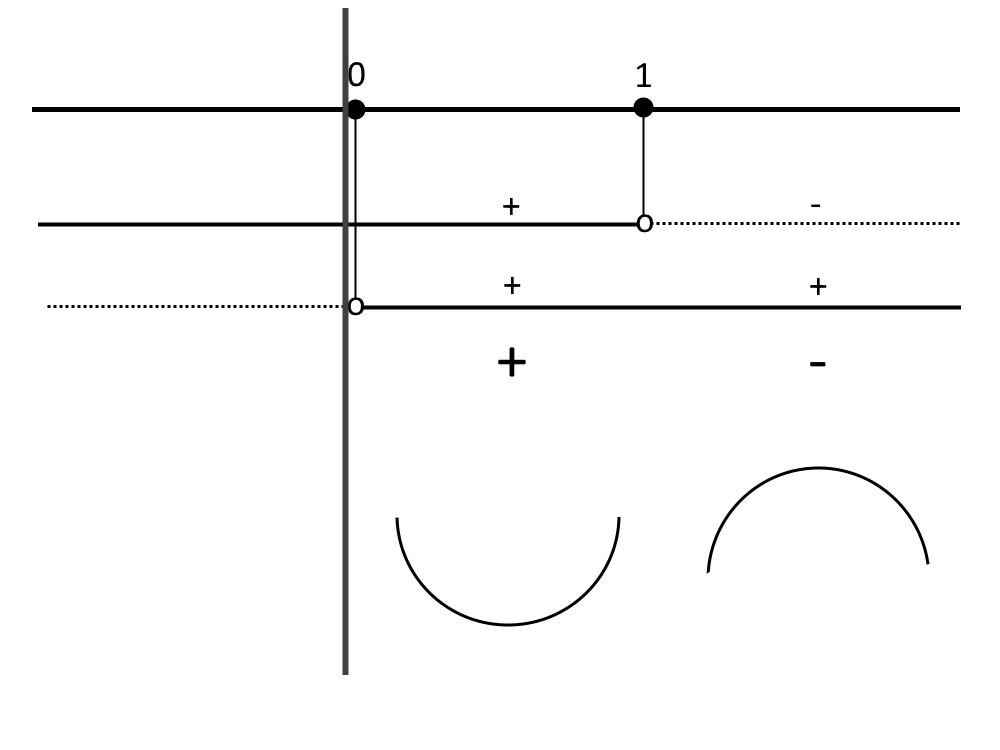
In 0<x<1 abbiamo la concavità verso l’alto, mentre in x>1 abbiamo la concavità verso il basso. x=1 è il punto dove si cambia concavità ed è detto anche flesso. Come vedete abbiamo escluso l’intervallo che non fa parte del dominio.
Esercizio 3. y=x^4 - \frac{1}{3} x^3 +2
Questa è una funzione polinomiale, e quindi definita in tutto R.
D: x \in \Reals
Ora passiamo al calcolo della derivata prima.
y'=4x^3 - \frac{1}{3}3 x^2 =4x^3 - x^2
E poi passiamo al calcolo della derivata seconda.
y''=12x^2 -2x
E studiamone il segno.
12x^2 -2x >0
Mettiamo in evidenza 2x:
2x(6x -1 )>0
Che risolviamo con un falso sistema.
\big\| 2x > 0 \\ \big\| 6x -1 > 0
\big\| x > 0 \\ \big\| x > \frac{1}{6}
Nello schema dei segni vediamo che:
L’intervallo x<0 è caratterizzato da concavità verso l’alto, l’intervallo 0<x< \frac{1}{6} ha concavità verso il basso, e poi in x> \frac{1}{6} ritorna ad avere la concavità verso l’alto, come in figura.
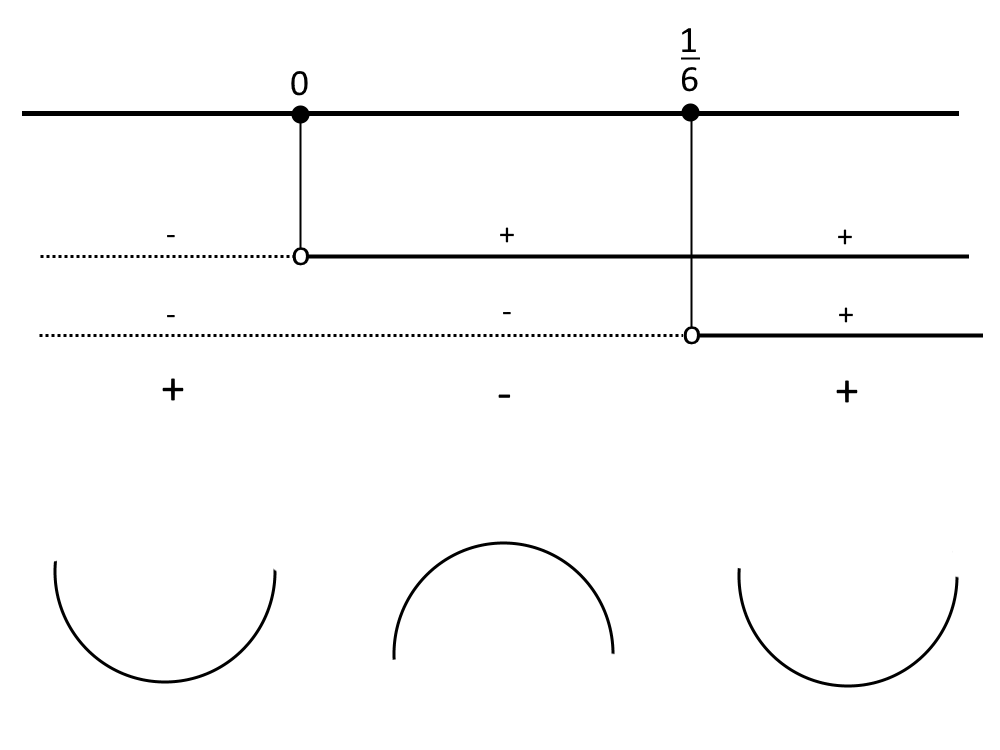
Continuiamo con altri esercizi svolti concavità funzioni!
Osservazione 4. Cosa succede se la funzione che ci dà la professoressa ha la derivata seconda troppo difficile ed impossibile da risolvere? Lo studio della concavità rappresenta l’ultimo passaggio dello studio di una funzione, quindi si può anche non fare se la derivata seconda non è fattibile. E’ assolutamente necessario fare la derivata prima e studiarne i massimi ed i minimi, ma la convessità non è obbligatoria! Chiaramente se essa è fattibile, bisogna farla! Questo è nei casi più difficili dove sono presenti frazioni complicate e con lunghissimi calcoli, quindi non disperate!
Esercizio 5. y=e^{2x} -2 e^x
Vi sono due funzioni esponenziali, per cui la funzione è definita in tutto R.
D: x \in \Reals
Passiamo al calcolo di y’.
y'=2e^{2x} -2 e^x
E poi y”.
y''=4e^{2x} -2 e^x
E ne studiamo il segno, come sempre.
4e^{2x} -2 e^x >0
Per risolverlo possiamo procedere per sostituzione, e porre t=e^x e quindi:
4t^2 -2t>0
E mettiamo in evidenza 2t.
2t(2t -1)>0
E questo, come visto negli esercizi precedenti, lo possiamo risolvere con un falso sistema.
\big\| 2t > 0 \\ \big\| 2t -1 > 0
\big\| t > 0 \\ \big\| t > \frac{1}{2}
Prima di studiare questo falso sistema, ritorniamo alla variabile x iniziale!
\big\| e^x > 0 \\ \big\| e^x > \frac{1}{2}
\big\| \forall x \\ \big\| x > \ln \frac{1}{2}
Il secondo termine, disequazione esponenziale, lo abbiamo risolto utilizzando la formula:
a^x > b \implies x> \log_a b
Ora ne studiamo i segni!
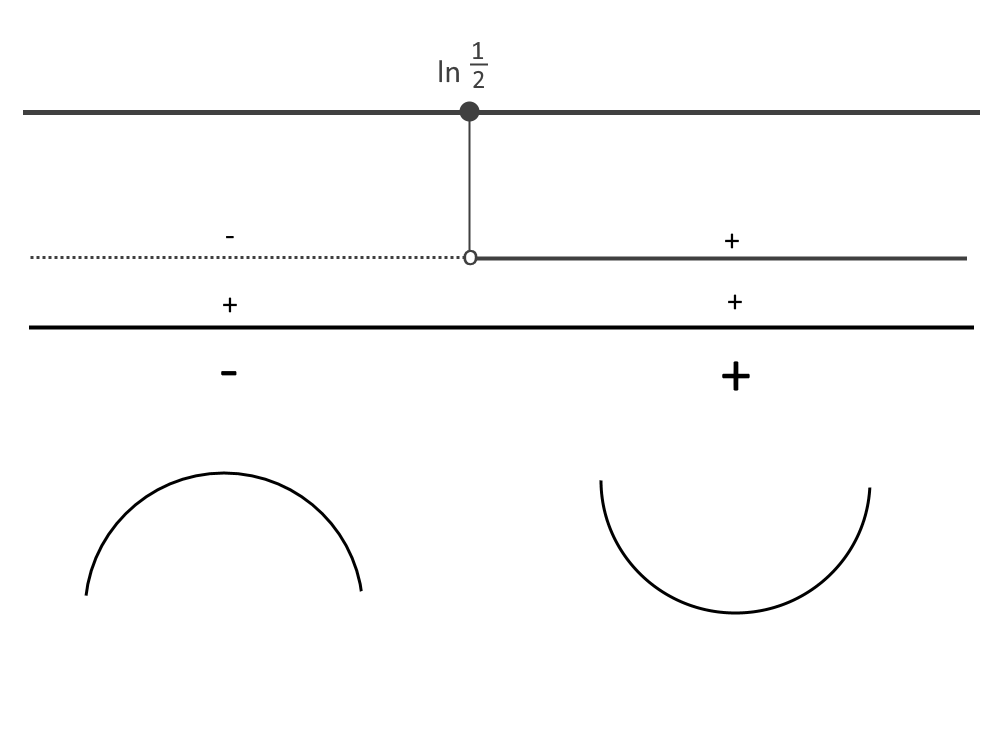
Notiamo che:
L’intervallo x< \ln \frac{1}{2} ha la concavità verso il basso;
l’intervallo x> \ln \frac{1}{2} ha la concavità verso l’alto.
Esercizio 6. y=2x \sqrt{x+1}
In questo esercizio abbiamo una funzione radice, quindi calcoliamone il dominio, cioè argomento positivo o uguale a zero:
D: x+1 \ge 0 \implies x \ge -1
Troviamo y’.
y'=2 \sqrt{x+1} + 2x \frac{1}{2 \sqrt{x+1} }
Facciamo il minimo comune multiplo, per rendere il tutto più compatto ovviamente.
y'= \frac{2(x+1) + x}{ \sqrt{x+1} } = \frac{3x+1 }{ \sqrt{x+1} }
Calcoliamo y”.
y''= \frac{ 3 \sqrt{x+1} -(3x+1) \frac{1}{2\sqrt{x+1}} }{ x+1 }
Come potete vedere il calcolo delle concavità si riduce molto a saper fare equazioni e disequazioni e derivate: importante è fare ogni passaggio controllando di non aver sbagliato qualche segno o dimenticato qualche pezzo!
Ora facciamo il minimo comune multiplo al numeratore:
y'' = \frac{ \frac{6(x+1)-(3x+1)}{2\sqrt{x+1}} }{ x+1 }= \frac{\frac{3x+3}{2\sqrt{x+1}}}{x+1}
Mettiamo in evidenza il 3 e semplifichiamo col denominatore.
y''= \frac{\frac{3(x+1)}{2\sqrt{x+1}}}{x+1} = \frac{3}{2\sqrt{x+1}}
Studiamone il segno y”>0.
\frac{3}{2\sqrt{x+1}} >0
Notiamo, senza fare nessun calcolo, che abbiamo un 3 ed un 2 che sono positivi chiaramente, e poi abbiamo una radice: studiamo solo la positività della radice:
\sqrt{x+1} > 0 \implies x+1 > 0 \implies x > -1
E proprio in questo intervallo, che è tra l’altro praticamente tutto il dominio, ha concavità positiva.
Continuiamo con altri esercizi svolti concavità funzioni!
Esercizio 7. y=2x - \arcsin x
Qui abbiamo un termine di polinomio, e poi abbiamo un arcseno che è definito nell’intervallo [-1,1]:
D: x \in [-1,1]
Facciamo la derivata.
y'=2 - \frac{1}{\sqrt{1-x^2}}
Qui non facciamo il minimo comune multiplo perchè se andiamo a derivare di nuovo il 2 se ne va e ci fa comodo. Calcoliamo subito y”.
y''= \frac{\frac{-2x}{2 \sqrt{1-x^2}}}{1-x^2} = - \frac{\frac{x}{ \sqrt{1-x^2}}}{1-x^2}
Porto il denominatore sopra.
y'' = - \frac{x}{ \sqrt{1-x^2}} (1-x^2 )
E poi applichiamo la proprietà delle potenze seguente:
\frac{a^b}{a^c} = a^{b-c}
E quindi nel nostro caso possiamo scrivere:
y''= - x(1-x^2 )^{\frac{1}{2}} = -x \sqrt{1-x^2}
Ora poniamo y”>0.
-x \sqrt{1-x^2}>0
\big\| -x > 0 \\ \big\| \sqrt{1-x^2} > 0
Il termine di radice è sempre >0 per definizione, tranne nei punti dove esso è uguale a zero, quindi:
\big\| x < 0 \\ \big\| \forall x \ne \pm 1
Ricordandoci il dominio, ossia che la funzione è definita nell’intervallo chiuso [-1,1], abbiamo quindi che:
Nell’intervallo -1<x<0 ha concavità verso l’alto, mentre nell’intervallo 0<x<1 ha concavità verso il basso, ossia negativa.
Esercizio 8. y=x + \arctg (x-1)
Qui abbiamo un arcotangente che non ha problemi di dominio, esso è definito in tutto R.
D: x \in \Reals
Calcoliamo allora la derivata prima.
y'=1 + \frac{1}{1+ (x-1)^2}
Anche in questo caso non facciamo nessun minimo comune multiplo, perchè tanto derivando ancora l’1 si leva. Deriviamo nuovamente per ottenere y”.
y''= \frac{-2(x-1)}{(1+ (x-1)^2)^2}
A questo punto studiamone il segno.
\frac{-2(x-1)}{(1+ (x-1)^2)^2} >0
Questo lo risolviamo come sempre con un falso sistema.
\big\| -2(x-1) > 0 \\ \big\| (1+ (x-1)^2)^2 > 0
Il secondo termine è sempre positivo per ogni x in R. Il primo, essendo -2 negativo, allora per essere il tutto positivo c’è bisogno che x-1 sia negativo anch’esso.
\big\| x-1 < 0 \\ \big\| \forall x
\big\| x < 1 \\ \big\| \forall x
Studiamo i segni, e notiamo che: in x<1 la funzione ha concavità positiva, verso l’alto. In x>1 la funzione ha la concavità verso il basso.
Esercizio 9. y= e^{\frac{x-1}{x+2}}
Abbiamo un esponenziale che quindi non ha problemi di dominio, però abbiamo anche una frazione, quindi:
D: x+2 \ne 0 \implies x \ne -2
Calcoliamo la derivata della funzione:
y'= \frac{(x+2)-(x-1)}{(x+2)^2} e^{\frac{x-1}{x+2}} = \frac{3}{(x+2)^2} e^{\frac{x-1}{x+2}}
Calcoliamo la derivata seconda adesso:
y''= - \frac{6}{(x+2)^3} e^{\frac{x-1}{x+2}} + \frac{9}{(x+2)^4} e^{\frac{x-1}{x+2}}
Se avete dei dubbi su questo tipo di derivate, vi consiglio di vedere gli esercizi derivate sugli esponenziali.
Adesso mettiamo in evidenza l’esponenziale:
y''= e^{\frac{x-1}{x+2}} [- \frac{6}{(x+2)^3} + \frac{9}{(x+2)^4} ]
E facciamo adesso il minimo comune multiplo all’interno della parentesi:
y''= e^{\frac{x-1}{x+2}} [\frac{-6(x+2)+9}{(x+2)^4} ] =e^{\frac{x-1}{x+2}} [\frac{-6x-3}{(x+2)^4} ]
Ed ora possiamo finalmente analizzare y”>0.
e^{\frac{x-1}{x+2}} [\frac{-6x-3}{(x+2)^4} ] >0
L’esponenziale è sempre positivo, il denominatore è sempre positivo: quindi l’unico a poter dare il segno è il numeratore:
-6x-3 >0 \implies x<-\frac{1}{2}
Disegniamo lo schema dei segni, inserendo sempre anche il dominio!
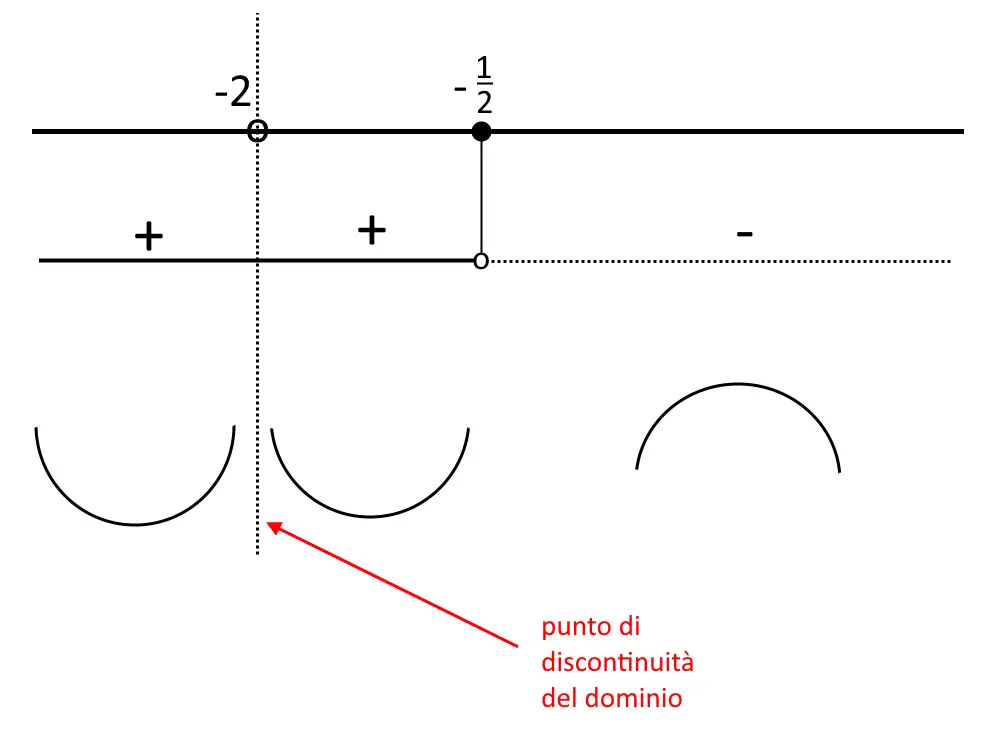
Come vedete c’è un punto di discontinuità del dominio. Lo schema ci fa capire che la funzione sia prima che dopo il punto di discontinuità ha concavità positiva…tutto qui.
Continuiamo con altri esercizi svolti concavità funzioni!
Esercizio 10. y= x \ln (x-1) -2
Abbiamo una funzione logaritmica, di conseguenza per il dominio bisogna porre l’argomento maggiore di zero:
D: x-1>0 \implies x>1
Adesso possiamo iniziare l’esercizio e andarci a calcolare le due derivate.
y'= \ln (x-1) + \frac{x}{x-1}
Calcoliamo ora direttamente y” senza fare altri passaggi, il minimo comune multiplo lo facciamo dopo, ora ci complicherebbe la vita.
y''= \frac{1}{x-1} + \frac{(x-1)-x}{(x-1)^2} = \frac{1}{x-1} - \frac{1}{(x-1)^2}
Ed ora conviene fare il minimo comune multiplo che ci siamo levati da mezzo anche il logaritmo!
y''= \frac{(x-1)-1}{(x-1)^2} = \frac{x-2}{(x-1)^2}
Poniamo y”>0.
\frac{x-2}{(x-1)^2} >0
Possiamo risolverlo sia per ragionamento che per falso sistema.
\big\| x -2>0 \\ \big\| (x-1)^2 >0
\big\| x >2 \\ \big\| \forall x \ne 1
Disegniamo lo schema dei segni, ricordandoci di inserire il dominio, ossia x>1. Quindi otteniamo che in 1<x<2 si ha concavità negativa, poi in x>2 concavità positiva.
Adesso vediamo degli esercizi svolti sullo studio delle concavità di una funzione goniometrica!
Calcolo concavità: funzioni goniometriche
Esercizio 11. y=3 \sin x in [0,2 \pi]
Anche per le funzioni goniometriche il discorso non cambia, seguiamo gli stessi passaggi. Teniamo a mente che le funzioni goniometriche, essendo periodiche (cioè che si ripetono con periodicità) non ha senso studiarle in tutto l’asse x, ma solo in un intervallo minimo di periodicità: ad esempio qui è [0,2 \pi] .
Il seno in questo intervallo non ha problemi di dominio o punti di discontinuità. Il dominio rimane quindi:
D: [0,2 \pi]
Iniziamo a calcolare la derivata prima:
y'=3 \cos x
E poi passiamo alla derivata seconda:
y''=-3 \sin x
Ora dobbiamo andare a studiare, come sempre, il segno della derivata seconda della funzione in gioco:
-3 \sin x > 0
Abbiamo una disequazione goniometrica. Cambiamo di segno e dividiamo per 3:
\sin x < 0
Disegniamo una circonferenza goniometrica, e notiamo che il seno è negativo nell’intervallo:
\pi < x < 2\pi
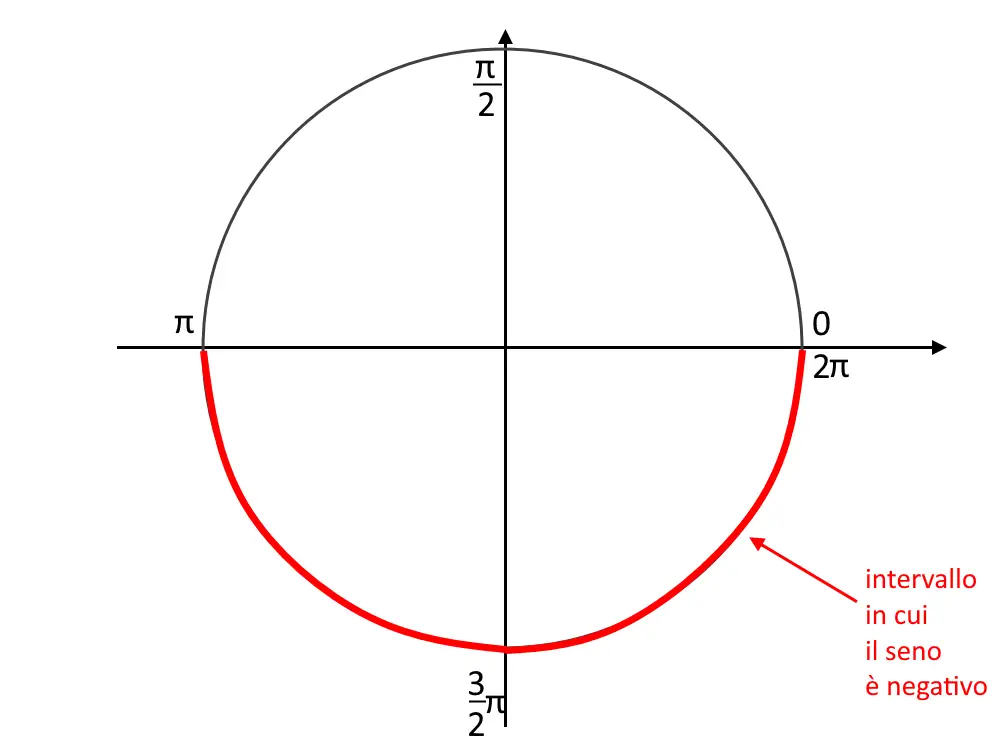
Disegniamo anche qui questo intervallo in uno schema dei segni (dove i valori vanno stanno nel dominio della funzione [0,2 \pi] ) come quello seguente:
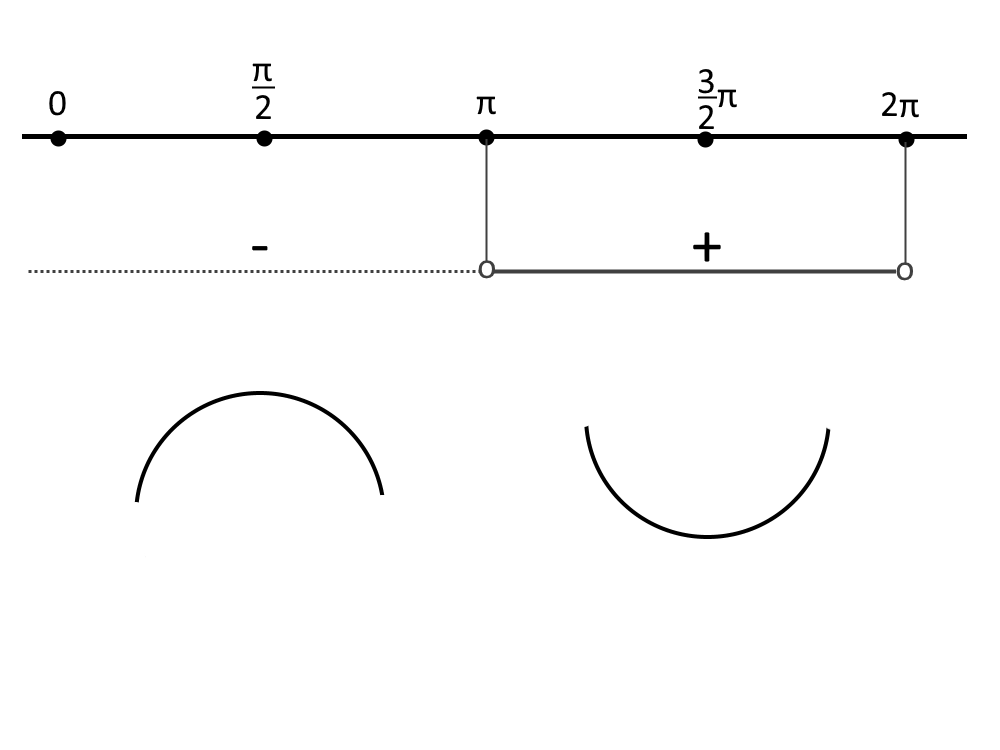
Quindi come potete vedere in 0 < x < \pi la concavità è verso il basso, mentre in \pi < x < 2\pi la concavità è verso l’alto, cioè positiva. Quindi di conseguenza il punto x=\pi è un punto di flesso, dove si cambia concavità.
Esercizio 12. y= \tg x in [0,\pi]
Calcoliamo il dominio della tangente il tale intervallo finito. La tangente presenta un punto di discontinuità in:
x \ne \frac{\pi}{2} +k \pi
Di conseguenza l’unico punto di discontinuità nell’intervallo di studio [0,\pi] è il punto x \ne \frac{\pi}{2} .
D: 0 \le x < \frac{\pi}{2} \land \frac{\pi}{2} < x \le \pi
Calcoliamo la derivata prima, potete vedere la derivata della tangente nella tabella.
y'= \frac{1}{ \cos^2 x }
Adesso possiamo passare al calcolo della derivata seconda. Riscriviamo però prima la frazione nella seguente maniera:
y'= ( \cos x )^{-2}
Quindi:
y''= -2( \cos x )^{-3} \cdotp (- \sin x) = \frac{2 \sin x}{ \cos^3 x }
E poi andiamo a studiarne il segno:
\frac{2 \sin x}{ \cos^3 x } > 0
Essa è una disequazione fratta, per cui andiamo a scrivere il suo falso sistema:
\big\| 2 \sin x > 0 \\ \big\| \cos^3 x > 0
\big\| \sin x > 0 \\ \big\| \cos x > 0
Basta disegnare una circonferenza goniometrica per rendersi conto in quale intervallo il seno ed il coseno sono maggiori di zero:
\big\| 0<x< \pi \\ \big\| 0<x< \frac{\pi}{2} \land \frac{3}{2} \pi < x < 2 \pi
Essendo il dominio compreso fra 0 e \pi possiamo anche riscrivere direttamente questo falso sistema come segue. Eliminando quindi la parte non compresa nel dominio chiaramente.
\big\| 0<x< \pi \\ \big\| 0<x< \frac{\pi}{2}
Facciamo il quadro dei segni e, tenendo conto del dominio (cioè del punto di discontinuità) otteniamo:
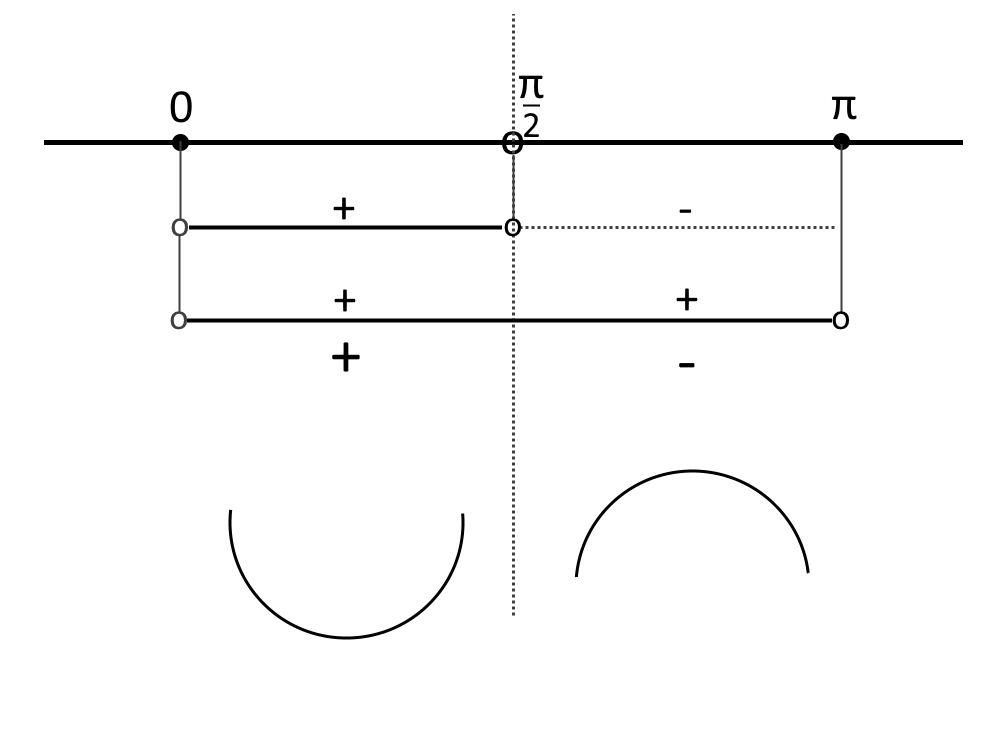
Continuiamo con altri esercizi svolti concavità funzioni!
Esercizio 14. y= \sin 2x in [0,\pi]
Qui la funzione è sinusoidale, e quindi problemi di dominio non ce ne sono: la funzione è ben definita in tale intervallo [0,\pi] .
Passiamo al calcolo della derivata prima:
y'= 2 \cos 2x
E poi passiamo alla derivata seconda:
y'= -4 \sin 2x
Poniamo maggiore di zero e studiamone il segno.
-4 \sin 2x > 0
Cambiamo di segno e dividiamo per 4:
\sin 2x < 0
Essendo che la parte dentro il seno non è solamente una x, ma abbiamo un 2x procediamo con una sostituzione.
Poniamo 2x=t e quindi la disequazione goniometrica diventa:
\sin t < 0
Questa è sicuramente molto più semplice da risolvere, il seno nella solita circonferenza goniometrica è negativo nell’intervallo:
\pi < t < 2 \pi
Riportiamo il tutto nella x:
\pi < 2x < 2 \pi
Dividiamo tutto per 2, quindi sia al centro che sinistra e destra, ed abbiamo così isolato la x.
\frac{ \pi }{2} < x < \pi
In tale intervallo la concavità è quindi verso l’alto, positiva. Nell’altro del dominio, ossia in 0<x<\frac{ \pi }{2}
è invece verso il basso, negativa.
Riassumiamo il tutto in una piccola tabella di consigli generali per l’esame e la verifica in classe!
Come risolvere esercizi sulle concavità

Questo era l’ultimo passo che ci porta ora a saper risolvere completamente un esercizio sullo studio di una funzione. Esso è argomento di esame, quindi continuate ad esercitarvi sul nostro sito: trovate esercizi svolti sia di matematica che altro ancora!
Per approfondire:
https://it.wikipedia.org/wiki/Funzione_concava
e minimi
esercizi
funzione
esercizi