Circonferenza: equazione ed esempi con spiegazione
In questa pagina vedremo la definizione di circonferenza, nel piano cartesiano. Poi vedremo l’equazione della circonferenza, e ci concentreremo su di essa, mostrando anche tanti esempi ed esercizi svolti. Tutto spiegato con cura, e con calma ed efficacia!
Indice
Iniziamo subito senza perdere tempo!
Circonferenza: definizione
Consideriamo un certo punto C, detto centro. La circonferenza è l’insieme di punti equidistanti dal centro C. L’insieme di punti forma una curva continua.
La distanza fra ogni punto della circonferenza ed il centro è costante, è sempre la stessa. Tale distanza, o lunghezza, è detto raggio.
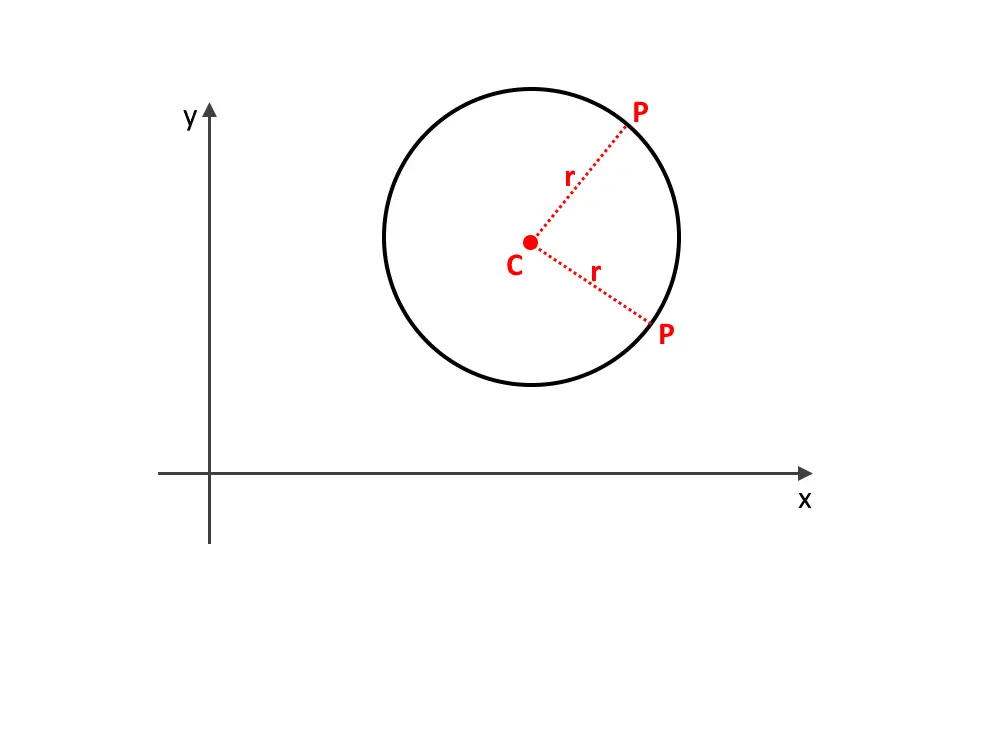
Matematicamente diremo che \overline{CP}=r=cost.. Questo è un primo passo per capire gli esercizi sulla circonferenza: il raggio è costante.
L’equazione della circonferenza
Consideriamo un piano cartesiano, disegniamo una circonferenza con centro C e raggio r. Una circonferenza, in un piano cartesiano, la rappresentiamo tramite la seguente equazione.
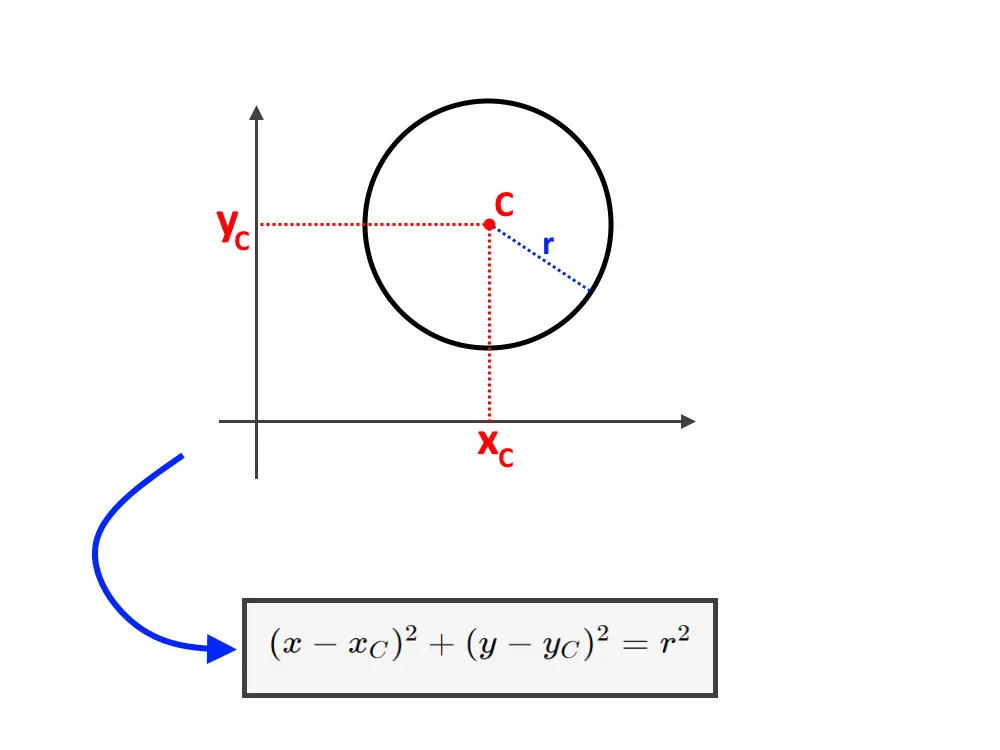
Questa equazione è utilissima e la useremo quando l’esercizio nominerà centro e raggio. C’è da dire che non è buona per fare il grafico per esempio. Possiamo trovare quindi un qualcosa di meglio. Vediamo!
L’equazione della circonferenza in questa forma, può in realtà essere scritta anche in un altro modo equivalente e migliore in molti casi. Cioè possiamo ricavare un’altra equazione per rappresentare la stessa circonferenza. Cos’ negli esercizi, a seconda di quale ci conviene, noi sceglieremo quale usare.
Notiamo infatti che vi compaiono due quadrati di binomio, quindi possiamo utilizzare la formula del quadrato del binomio, per scriverla in un altra forma.
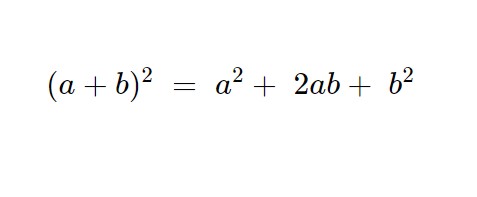
Nel nostro caso otteniamo:
x^2 +x_C ^2 -2x_C x + y^2 +y_C ^2 -2y_C y = r^2
Portiamo il raggio a primo membro:
x^2 +x_C ^2 -2x_C x + y^2 +y_C ^2 -2y_C y - r^2 = 0
Adesso possiamo effettuare delle sostituzioni comode, per semplificare il tutto in una nuova scrittura migliore:
\begin{cases}a=-2x_C \\ b= - 2y_C \\ c=x^2 +y^2 -r^2 \end{cases}
Otteniamo, dopo queste sostituzioni una nuova forma, sotto rappresentata.
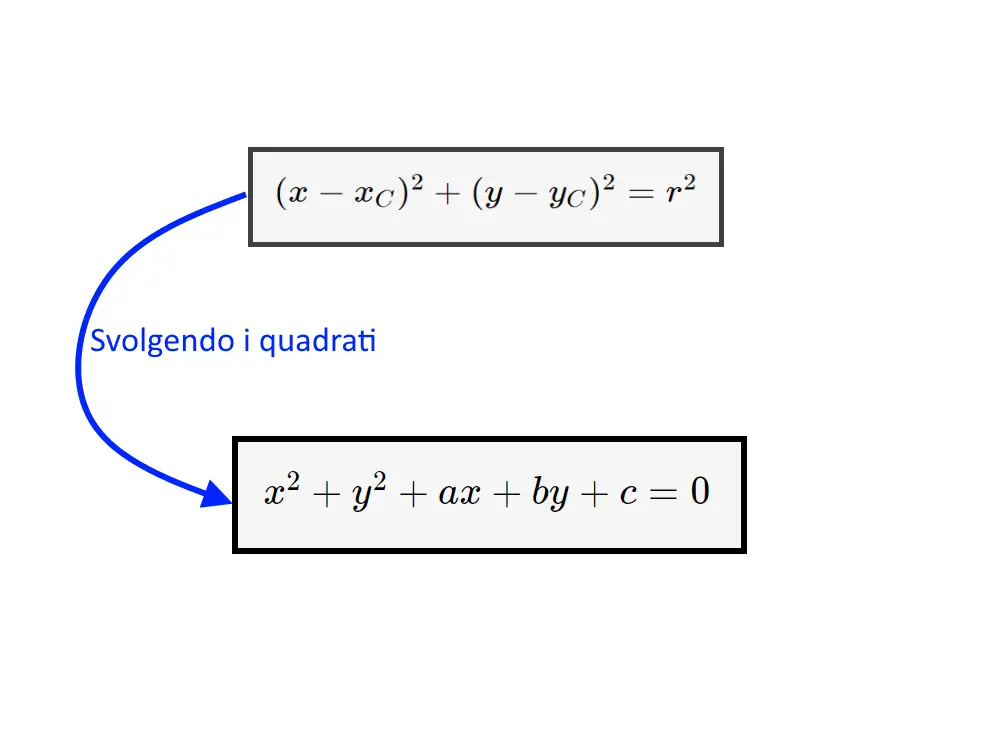
Questa rappresenta la stessa circonferenza, scritta semplicemente in un modo alternativo, detta in forma implicita. Questa può risultare più comoda in molti casi. C’è da considerare che se l’esercizio ci nomina centro e raggio, allora è sicuramente meglio partire dall’altra! Abbiamo nominato “partire”, perché se l’esercizio vi chiede “determinare l’equazione della circonferenza” vi sta chiedendo la seconda equazione.
Possiamo notare che essa è caratterizzata dall’avere i termini quadratici con coefficienti uguali (ossia x^2 e y^2 senza numeri prima).
Quindi per la circonferenza abbiamo due equazioni che possiamo usare! Ricordate che queste due equazioni rappresentano la stessa identica circonferenza!
A nostra scelta, decideremo se iniziare con una o l’altra. Alla fine dei conti è però meglio finire con il ricavare la seconda equazione. Ma capiremo tutto negli esercizi svolti di dopo!
E’ necessario che ci sia 1 come coefficiente dei termini quadratici? In realtà se abbiamo ad esempio:
3x^2 + 3y^2 + 2x +2y +3 =0
Va bene lo stesso! Basta che i coefficienti quadratici siano uguali! Questo perché se dividiamo tutto per 3:
x^2 + y^2 + \frac{2}{3}x +\frac{2}{3}y +1 =0
E siamo ritornati all’equazione classica di una circonferenza!
Quindi basta che siano uguali!
E se invece l’esercizio ci dà questo? Supponiamo che l’esercizio ci dia:
(x-3)^2+ (y-2)^2 = -2
Questa equazione è riconducibile alla prima equazione della circonferenza detta. In realtà questa non è una circonferenza. A destra ci deve stare il r^2, ed un raggio al quadrato deve essere positivo. Qui abbiamo -2, quindi questa equazione non rappresenta una circonferenza.
L’equazione seguente rappresenta una circonferenza?
x^2 + y^2 = 9
La risposta è sì! Per capirlo dobbiamo metterlo a confronto con, ad esempio, l’equazione di una generica circonferenza:
(x-x_C)^2+ (y-y_C)^2 = r^2
E per confronto, notiamo che:
Il centro è C=(0,0). Il raggio è:
r^2 = 9 \implies r= \sqrt{9} = 3
Attenti che nella formula c’è scritto il raggio al quadrato!
Adesso, siamo pronti per degli esercizi! Abbiamo capito tante cose, quindi applichiamole!
Esercizi svolti e spiegati sull’equazione della circonferenza
Esercizio 1. Scrivi l’equazione della circonferenza, con centro C=(-3,1) e con raggio r= \sqrt{5} .
Allora, partiamo col dire una cosa: l‘esercizio ci parla di raggio e di centro, quindi partiremo con la seguente equazione per rappresentare la circonferenza:
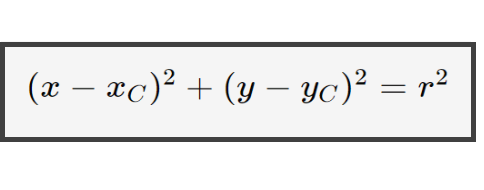
Ciò che dovremmo fare è semplicemente sostituire i dati che abbiamo nell’equazione di sopra:
(x-(-3))^2+ (y-1)^2 = \sqrt{5}^2
La radice se ne va, inoltre notiamo che abbiamo messo una parentesi davanti al -3. E’ sempre meglio fare così quando ci sono più segni meno, sempre per non confondersi e fare errori.
(x+3)^2+ (y-1)^2 = 5
L’esercizio non è concluso, perché quando un esercizio ci chiede “determina l’equazione della circonferenza” ci sta chiedendo la seconda equazione.
Per trovarla, svolgiamo semplicemente i calcoli, partendo da questa.
x^2+9 -6x+ y^2+1 +2y = 5
Portiamo tutto a primo membro e sommiamo i rispettivi termini simili:
x^2+ y^2 -6x +2y +5 = 0
Questa è l’equazione della circonferenza!
Esercizio 2. Individua l’equazione della circonferenza con centro in origine e raggio \sqrt{\frac{3}{2}}.
L’esercizio ci sta dicendo che il centro C della circonferenza sta nell’origine, ossia in C=(0,0).
Ci dice anche il raggio, quindi utilizziamo la prima equazione:
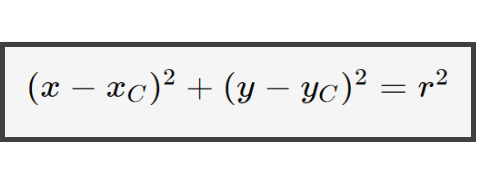
Sostituendo otteniamo:
x^2 + y^2 = \frac{3}{2}
E portando a primo membro abbiamo così l’equazione della circonferenza in forma implicita:
x^2 + y^2 - \frac{3}{2} = 0
Esercizio 3. Scrivi l’equazione della circonferenza con centro C=(2,-3) e raggio 4.
Provatelo a fare voi! E poi rivenite a controllare! Questo esercizio è uguale al primo, quindi seguiamo lo stesso procedimento.
(x-2)^2+ (y-(-3))^2 = 4^2
(x-2)^2+ (y+3)^2 = 16
Svolgiamo i calcoli, e ricaveremo l’equazione della circonferenza in forma implicita:
x^2 +4 -4x+ y^2+9 -6y = 16
x^2 +4 -4x+ y^2+9 -6y - 16 =0
Sommiamo ed abbiamo fatto!
x^2 + y^2-4x -6y - 3 =0
Esercizio 4. Scrivi l’equazione della circonferenza di centro C(0,3) e passante per P(2,-1).
Il problema ci sta dando il centro, però ci manca il raggio! Come lo troviamo? Se la circonferenza è passante per P, allora significa che il raggio è r = \overline{CP} . Il disegno aiuta sempre nei momenti di difficoltà!
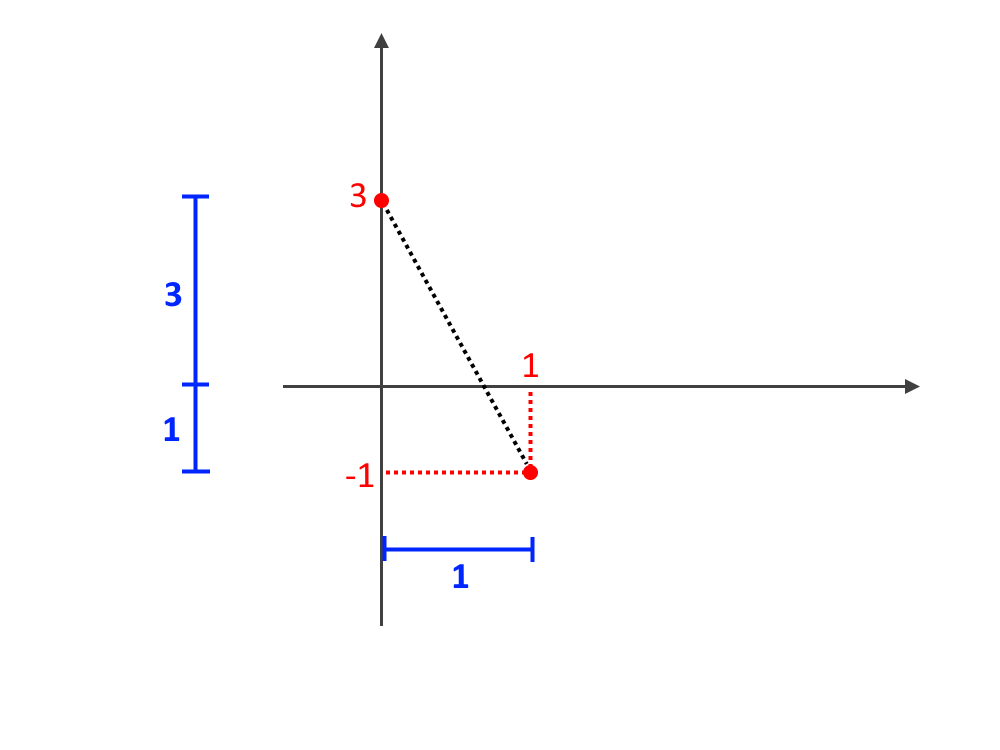
Utilizzano il Teorema di Pitagora sul triangolo formatosi, possiamo ricavare l’ipotenusa, ossia il raggio.
r= \overline{CP} = \sqrt{4^2 + 2^2 } = \sqrt{16+4} = \sqrt{20}
Perché 4? Perché bisogna sommare 3 e poi 1 (la coordinata è -1, ma qui stiamo considerando la lunghezza, che è definita positiva: qualcosa non può essere lunga -3 per es.)
Ora che abbiamo trovato anche il raggio abbiamo tutto!
(x-0)^2+ (y-3)^2 = \sqrt{20}^2
x^2+ (y-3)^2 = 20
Svolgiamo il quadrato del binomio:
x^2+ y^2+9 -6y = 20
x^2+ y^2 -6y -11 = 0
Manca qualche termine ma non fa nulla, è dovuto al fatto che una componente del centro è 0.
La pagina è conclusa. Speriamo vi sia stato chiaro tutto!
Trovate tanto altro nel nostro sito, di Matematica, di Geometria analitica e Geometria!
Continuate a supportare il nostro sito!
di rette
esercizi
parabola
calcolo