Esercizi svolti sul fascio di rette
In questa pagina vediamo degli esercizi svolti e spiegati in ogni singolo passaggio sul fascio di rette. Basta seguire questa pagina per essere immediatamente pronti per la verifica in classe! Ma iniziamo subito col primo esercizio!
Esercizio 1. Studia le caratteristiche del fascio di rette di equazione:
(2+k)x - (1+k)y -5-k = 0
Studiare un fascio di rette significa determinarne le proprietà: trovare le generatrici, fascio proprio o improprio, centro del fascio.
Partiamo dal trovare le rette generatrici. Un fascio generato da due rette ha la seguente forma:
ax+by+c + k(a'x+b'y+c') = 0
Con scritte al suo interno le equazioni delle due rette generatrici in forma implicita. Quindi ciò che dovremo fare è ricavare questa forma. Per farlo alla fine dovremo mettere in evidenza il k. Ma ora dobbiamo prima levare tutte quelle odiose parentesi tonde:
2x+kx -y-ky -5-k = 0
Ora possiamo mettere in evidenza k:
2x -y-5 +k(x-y-1) = 0
La prima retta generatrice è quello che vediamo a sinistra, la seconda è quella in parentesi.
r: \; 2x-y-5=0
s: \; x-y-1=0
Adesso bisogna determinare se il fascio è proprio o improprio.
Perché prima questo passaggio? Perché se il fascio è improprio (ossia rette parallele) non c’è bisogno di trovare il centro del fascio visto che non c’è!
Per farlo dobbiamo vedere una cosa. Come detto nella pagina di teoria del fascio di rette, (c’è tutto lì, cliccateci) un fascio è proprio se:
\frac{a}{b} \ne \frac{a'}{b'}
E sarà improprio se:
\frac{a}{b} = \frac{a'}{b'}
Quindi vediamo! Sostituiamo i coefficienti delle nostre due rette:
\frac{2}{-1} = \frac{1}{-1}
E chiaramente notiamo che sono diversi!
-2 \ne -1
Quindi il fascio è proprio! Ci sarà quindi un centro da calcolare! Il centro del fascio corrisponde anche al punto di intersezione delle due rette generatrici.
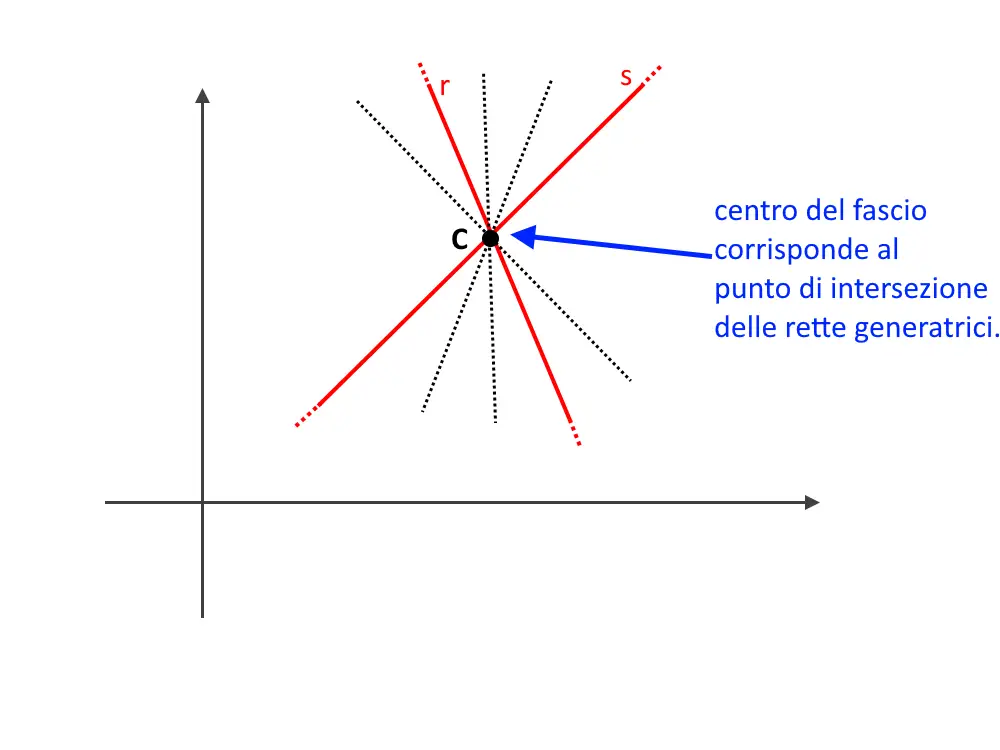
Quindi semplicemente, calcoliamo l’intersezione fra queste due rette, mettendole a sistema:
\begin{cases} 2x-y-5 = 0 \\ x -y -1 = 0 \end{cases}
Scegliamo di risolverlo per confronto, quindi mettiamo tutto a secondo membro tranne la y:
\begin{cases} -y = -2x+5 \\ -y = -x+1 \end{cases}
Cambiamo di segno:
\begin{cases} y = 2x-5 \\ y = x-1 \end{cases}
E poi li mettiamo a confronto (se non vi ricordate queste cliccate qui).
\begin{cases} y = 2x-5 \\ 2x-5 = x-1 \end{cases}
Risolvendo quella equazione, troviamo la x, ossia la componente x del centro del fascio:
\begin{cases} y = 2x-5 \\ x = 4 \end{cases}
Dopo di che mettiamo il valore di 4 al posto della x nella prima equazione. Troviamo così la componente y del centro del fascio:
\begin{cases} y = 3 \\ x = 4 \end{cases}
Il centro del fascio è C=(4,3) .
Esercizio 2. Dato il fascio di rette di equazione (k-3)x + (2k+2)y +1-3k=0 . Determina:
- le equazioni delle generatrici e il centro;
- le rette del fascio che incontrano l’asse x in un punto A tale che \overline{AO} = 3 ;
- il valore di k corrispondente alla retta parallela all’asse x.
Svolgimento. Il problema ci chiede le equazioni delle generatrici: ciò significa che questo problema è relativo al fascio generato da due rette. Come spiegato nella pagina di teoria & esempi del fascio di rette, un fascio generato da due rette, con un solo parametro ha la seguente forma:
ax+by+c + k(a'x+b'y+c') = 0
Dove le equazioni delle rette generatrici sono ax+by+c e l’altra è a’x+b’y+c’. Di conseguenza leviamo un attimo le parentesi nella nostra equazione:
kx-3x + 2ky+2y +1-3k=0
Dopo di che, per confronto, mettiamo in evidenza il k:
-3x +2y +1+k(x+2y-3)=0
In questo modo abbiamo ottenuto la classica forma di un fascio generato da due rette! Notiamo allora che le due rette generatrici sono:
r: \; -3x +2y +1 = 0
s: \; x +2y -3 = 0
Adesso il problema ci chiede di calcolare il centro del fascio. Il centro del fascio è anche lo stesso punto che rappresenta il punto di intersezione fra queste due rette (tutte queste cose stanno scritte nella teoria del fascio di rette).
Quindi calcoliamolo!
\begin{cases} -3x +2y +1 = 0 \\ x +2y -3 = 0 \end{cases}
Decidiamo di risolvere questo sistema per confronto (potete scegliere il metodo che volete). Quindi isoliamo la y a sinistra:
\begin{cases} 2y = 3x-1 \\ 2y = 3-x \end{cases}
E poi mettiamo in uguaglianza i membri che sono uguali (se non vi ricordate questo metodo, potete anche andare per sostituzione, cliccate qui per una ripassata):
\begin{cases} 2y = 3x-1 \\ 3x-1 = 3-x \end{cases}
Svolgendo quella equazione, ci troviamo la x:
\begin{cases} 2y = 3x-1 \\ x = 1 \end{cases}
E poi sostituiamo questo valore della x nella prima equazione, e ci troviamo la y:
\begin{cases} 2y = 3-1 \\ x = 1 \end{cases}
\begin{cases} y = 1 \\ x = 1 \end{cases}
Questa è la coppia di componenti del punto di intersezione fra le due rette generatrici, che sono anche il centro del fascio! Il punto è C=(1,1) .
Adesso passiamo al secondo punto che ci chiede il problema. Ci chiede di trovare le rette del fascio che incontrano l’asse x in un punto A, tale che \overline{AO} = 3 . Spieghiamo una cosa per volta.
Tutte le rette del fascio passano per il centro giusto? Esatto. Queste rette devono però anche passare nel punto A. Questo punto A sta sull’asse x, ed inoltre dista dal centro O una distanza di 3. La traccia è un poco a trabocchetto perché i punti che stanno sopra l’asse x e che distano 3 ne sono ben due, come in figura!
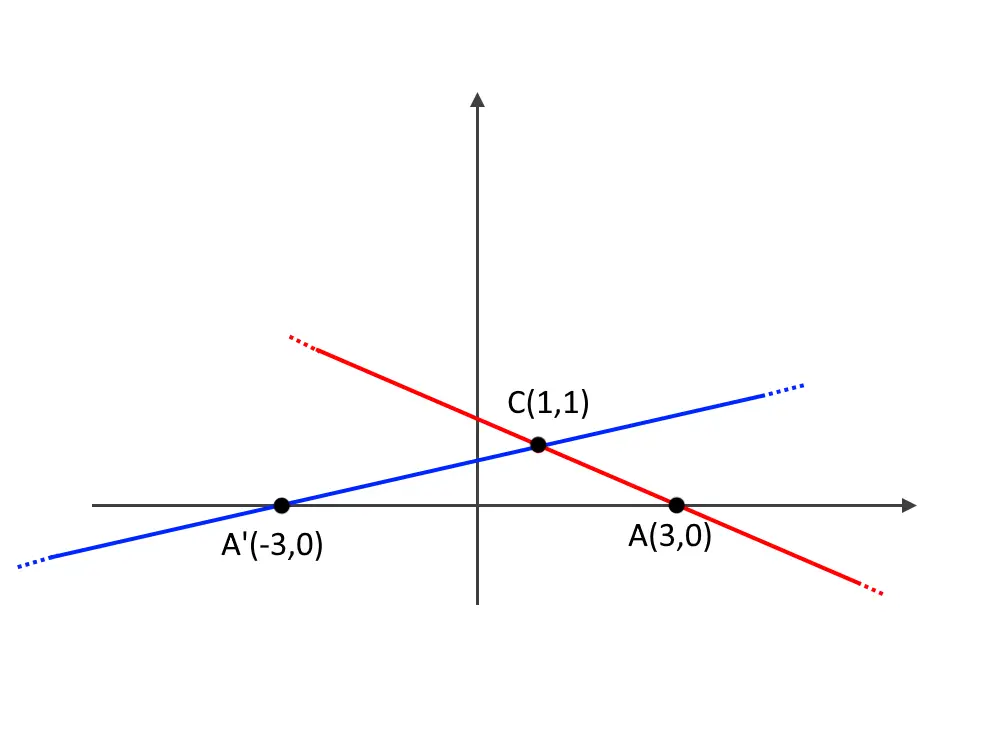
Quindi avremo due rette da calcolare! Il punto A assume due posizioni differenti. Possiamo chiamare il primo punto A ed il secondo A’.
Ma \overline{A'O} =-3? Assolutamente no! Quel segno sopra A’O sta ad indicare una lunghezza, che per definizione è positiva.
Capiamo facilmente dal disegno (fate sempre i disegni!) che i punti A e A’ hanno di coordinate:
A=(-3,0), A'=(3,0)
(Stando sull’asse x, il valore della y è 0)
Adesso quindi abbiamo una retta passante per i due punti A e C: possiamo usare la formula della retta passante per due punti per calcolarne l’equazione.
\frac{y-y_A}{y_C -y_A} = \frac{x-x_A}{x_C -x_A}
Sostituiamo i dati dei punti A=(-3,0),C=(1,1)
\frac{y-0}{1 -0} = \frac{x-(-3)}{1 -(-3)}
y = \frac{x+3}{4}
Moltiplico tutto per 4, così leviamo la frazione.
4y = x+3
E poi se volete in forma implicita portiamo semplicemente tutto a primo membro cambiando di segno:
x-4y+3 = 0
E questa è l’equazione della prima retta, ossia quella passante per i punti A ed C.
Adesso facciamo lo stesso procedimento, ma con i punti A'=(3,0),C=(1,1) .
\frac{y-0}{1 -0} = \frac{x-3}{1 -3}
y = \frac{x-3}{-2}
E come prima, ricaviamo poi:
-2y = x-3
x+2y-3 = 0
Dove per comodità cerchiamo sempre di tenere la x positiva.
Passiamo all’ultimo punto. Ci chiede il valore di k per la retta parallela all’asse x. Qui è comodissimo ritornare alla traccia del problema:
(k-3)x + (2k+2)y +1-3k=0
Questo perché? Una retta che è parallela all’asse x, ha il coefficiente della x pari a zero. Cioè se una retta è parallela all’asse x, nella sua equazione la x non deve comparire. Quindi vogliamo che la x scompaia. E scompare ponendo a zero il suo coefficiente:
k-3 = 0 \implies k=3
Ecco fatto!
Esercizio 3. Studia il fascio di rette di equazione (k+2)x + (2-k)y +3-k = 0 e determina per quali valori del parametro k la retta del fascio:
- passa per l’origine;
- è parallela alla retta y=3;
- è perpendicolare alla retta 2x+3y-4=0;
- incontra la retta di equazione x+4y-1=0 nel punto di ordinata 1;
- è parallela alla retta passante per (-1,1) e (2,-1).
Svolgimento. Partiamo dal punto 1. Dobbiamo trovare per quale valore di k vi è una retta che passa per l’origine. Una retta che passa per l’origine ha la tipica forma di y=mx. Ossia non c’è il termine noto. Quindi dobbiamo fare lo stesso con il fascio di rette: dobbiamo eliminare il suo termine noto.
(k+2)x + (2-k)y +3-k = 0
Il termine noto è ciò che non è legato ad x oppure ad y, quindi è:
3-k
E noi vogliamo che questo faccia zero, così la retta risultante avrà la forma classica di una retta passante per l’origine.
3-k=0 \implies k=3
Passiamo al secondo punto. Per quale valore di k si ha una retta parallela a y=3? Una retta che è parallela a y=3 significa che è parallela all’asse x.
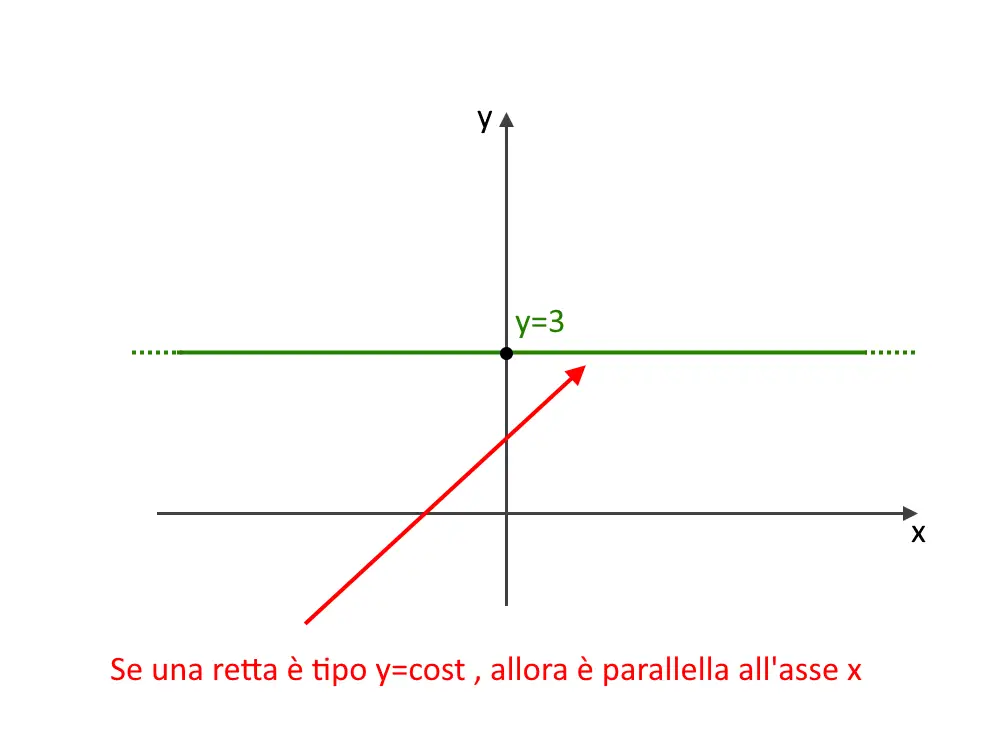
Una retta parallela all’asse x è una equazione che non contiene la x. Ossia può essere y=2, y=3 ecc. non ci deve stare la x!
DI conseguenza partendo sempre dal fascio:
(k+2)x + (2-k)y +3-k = 0
Questa volta poniamo a 0 il coefficiente della x.
k+2=0 \implies k=-2
Punto 3. Dobbiamo trovare la retta perpendicolare a 2x+3y-4=0. Una retta è perpendicolare ad un’altra se:
aa' + bb' = 0
Questa formula e questo argomento lo trovate nella pagine delle rette perpendicolari.
Quindi basterà semplicemente sostituire i coefficienti del fascio (con a ed b) e della retta (con a’ ed b’):
(k+2)2 + (2-k)3 = 0
E questa è una equazione di primo grado da risolvere!
2k+4 + 6-3k = 0 \implies k=10
Tutto qui! Adesso passiamo al punto numero 4. Nella traccia il termine incontrare vi deve far venire in mente l’intersezione. Quindi mettiamo a sistema fascio (dove dobbiamo trovare la k) e retta, per trovare l’incontro fra le due rette.
\begin{cases} (k+2)x + (2-k)y +3-k = 0 \\ x+4y-1=0 \end{cases}
Questo è un sistema di due equazioni…ma con tre incognite! Quindi non sarà mai risolvibile. Come facciamo? Il problema ci viene incontro dicendoci che si intersecano nel punto di componente y=1, quindi possiamo sostituire questo valore alla y nel sistema!
\begin{cases} (k+2)x +2-k +3-k = 0 \\ x+4-1=0 \end{cases}
Sommiamo ciò che si può sommare:
\begin{cases} (k+2)x +5-2k = 0 \\ x+3=0 \end{cases}
Dalla seconda equazione ricaviamo anche la x:
\begin{cases} (k+2)x +5-2k = 0 \\ x=-3 \end{cases}
E sostituiamo tale valore nella prima, così troveremo il k!
\begin{cases} -3(k+2) +5-2k = 0 \\ x=-3 \end{cases}
Concentriamoci solo sulla prima, che è quella che ci serve!
-3k-6 +5-2k = 0
-5k = 1 \implies k = - \frac{1}{5}
Adesso passiamo all’ultimo punto. E’ parallela alla retta passante per i due punti A=(-1,1) e B=(2,-1). Iniziamoci a trovare l’equazione di questa retta usando la formula della retta passante per due punti:
\frac{y-y_A}{y_B -y_A} = \frac{x-x_A}{x_B -x_A}
Sostituiamo i dati che abbiamo:
\frac{y-1}{-1 -1} = \frac{x-(-1)}{2 -(-1)}
\frac{y-1}{-2} = \frac{x+1}{3}
Moltiplichiamo per -2 e poi per 3, così da sbarazzarci delle frazioni.
3y-3 = -2x-2
2x+3y-1 = 0
Ed eccola qua! Ora passiamo alla parte importante: questa deve essere parallela ad una del fascio. Due rette sono parallele se:
ab' -a'b = 0
Sostituiamo i rispettivi coefficienti:
(k+2)3 -2(2-k) = 0
3k+6 -4+2k = 0 \implies k = - \frac{2}{5}
Esercizio concluso, lunghetto…ma bastano pochi per capire! Sono più o meno sempre le stesse cose.
La pagina sugli esercizi svolti sul fascio di rette è terminata. Speriamo vi sia stato tutto chiaro. Non è un argomento semplice, e lo capiamo.
Trovate altri centinaia di argomenti di Matematica, Geometria analitica e Geometria.
Continuate a supportare il nostro sito!
di rette