Codominio di una funzione: COME SI TROVA e CALCOLA
In questa pagina vedremo come si trova e calcola il codominio di una funzione. Non ci limiteremo solo a mostrarvi il procedimento per calcolare il codominio, ma vi daremo tantissimi esercizi svolti, così che possiate al meglio capire come si svolgono questi tipi di esercizi.
Indice
- Codominio ed Immagine sono la stessa cosa?
- Come si trova il codominio di una funzione
- Esercizi svolti
Detto ciò, rimbocchiamoci le maniche ed iniziamo a vedere come muoverci negli esercizi del codominio di una funzione!
Codominio ed Immagine sono la stessa cosa?
Prima di iniziare a vedere degli esercizi svolti sul come si trova il codominio di una funzione, dobbiamo chiarire alcuni dubbi. C’è tanta confusione purtroppo sui libri e su internet: a volte dicono immagine ed altre volte dicono codominio, ma sono la stessa cosa? Hanno procedimenti diversi?
La risposta è immediata, e vi chiariamo subito ogni dubbio. Se andate ad un Liceo, negli esercizi per voi codominio ed immagine sono la stessa cosa! Per semplificarvi la vita, i libri l’hanno resi uguali.
Nella pagina sul dominio e codominio, abbiamo specificato la loro differenza, ma una volta negli esercizi, purtroppo alcuni usano la parola “codominio” ed altri “immagine”, ma intendono la stessa cosa, quindi state tranquilli e seguite i procedimenti di questi esercizi svolti.
Più precisamente andremo a calcolare l’immagine di una funzione, cui però molto spesso si trova al suo posto la parola “codominio”.
Se andate all’Università, dovete approfondire meglio la situazione, e vi invito a cliccare qui. Lì purtroppo non sono esattamente la stessa cosa, quindi dovete fare attenzione.
Come si trova il codominio di una funzione
Ora che ci siamo chiariti dei dubbi, vediamo insieme il procedimento generale e guidato sul come si trova e calcola il codominio di una funzione. In questa sezione commenteremo ogni singolo passaggio.
Il libro ci dirà di solito “determina il codominio” della funzione seguente. Per esempio:
y = \frac{x^2 -2}{x}
Il PRIMO PASSAGGIO è: trovare il Dominio della funzione. Ebbene sì, prima del codominio, bisogna sempre trovare il dominio della funzione. I professori spesso lo segnano come errore.
Qui abbiamo una funzione fratta, per cui il dominio della funzione fratta è semplicemente il denominatore diverso da zero.
D: x \ne 0
Solo dopo aver trovato il dominio, possiamo andare avanti con l’esercizio.
SECONDO PASSAGGIO: troviamo x(y). Questo è più facile a farsi che a dirsi, dobbiamo in pratica portare la x a sinistra e la y a destra, ed avere un qualcosa del tipo x=…y… In questo passaggio la y la consideriamo come costante, come numero, e quindi ci facciamo quello che vogliamo.
Partendo dalla funzione che ci dà il libro, in questo caso ci dà:
y = \frac{x^2 -2}{x}
Dobbiamo isolare la x a sinistra in breve. Per far ciò bisogna un po’ manipolare la funzione. Iniziamo a moltiplicare tutto per x, così ci leviamo di torno la frazione che dà sempre fastidio:
xy = x^2 -2
Portiamo tutto a primo membro:
-x^2 +2 +xy = 0
-x^2 +xy +2 = 0
Supponendo appunto, come detto prima, che la y la consideriamo costante per questo passaggio, allora quella che vediamo è una equazione di secondo grado! E quindi la risolviamo normalmente. Iniziamo quindi a cambiare di segno tutto. Se non vi ricordate come si fanno, cliccateci un attimo e vi date una rinfrescata.
x^2 - xy -2 = 0
Troviamo il Delta:
\Delta = b^2 - 4ac = (-y)^2 - 4 \cdotp 1 \cdotp (-2) = y^2 +8
E quindi la x sarà, secondo la formula:
x = \frac{-b \pm \sqrt{\Delta} }{2a} = \frac{y \pm \sqrt{ y^2 +8 } }{2}
Notiamo insieme che siamo riusciti a ricavare la x a sinistra, e la y da sola a destra. Abbiamo quindi invertito tutto. Questo era il secondo passaggio!
TERZO PASSAGGIO: Trovo il CODOMINIO della funzione nuova trovata. Questo è un semplice passaggio che sappiamo fare. Abbiamo:
x = \frac{y \pm \sqrt{ y^2 +8 } }{2}
In sintesi, dobbiamo calcolare il “dominio” di questa nuova funzione, facendo quindi gli stessi passaggi e ragionamenti che sapete fare voi per trovare il dominio.
Solo che questa volta abbiamo a destra y, e quindi si chiama codominio. Ma i passaggi sono uguali!
A destra abbiamo una funzione radice. Il suo dominio (che ora si chiama codominio perché abbiamo y) è radicando maggiore o uguale di zero:
C: y^2 + 8 \ge 0 \implies y^2 \ge -8
Essendo che una quantità quadrata è sempre positiva, è sempre maggiore di -8 e quindi è vera per qualsiasi valore di y, ossia:
C: y \in \Reals
RICAPITOLANDO L’ULTIMO PASSAGGIO: L’ultimo passaggio non è difficile. E’ come se fosse un normale esercizio sul “trova il dominio“, e dovete seguire le stesse formule che conoscete.
L’unica cosa che cambia è che avete una y adesso, e quindi per differenziare le due cose, lo chiamiamo calcola il codominio, tutto qui. Riassumiamo il tutto nel seguente schema.

So che potreste avere ancora alcuni dubbi, quindi leggete i prossimi esercizi svolti, così ci chiarite le idee!
Calcolo Codominio: ESERCIZI SVOLTI
Esercizio 1. Trova il codominio di y = x^2 +1
Come prima cosa, andiamo a trovare il dominio. Discutiamo insieme: abbiamo una funzione polinomiale, e che non dà problemi, per cui il dominio è il seguente.
D: x \in \Reals
Passiamo ora al secondo passaggio, quello in cui dobbiamo portare la x a sinistra ed isolarla. Qui i passaggi sono più brevi, e portiamo la y a destra:
-x^2 = 1 -y
L’obiettivo finale, vi ricordiamo, è quello di avere un qualcosa del tipo x=…..Quindi iniziamo a cambiare anche di segno:
x^2 = y-1
Considerando la y sempre come una costante, e quindi come numero, qui dobbiamo usare la seguente formula di risoluzione per una equazione di secondo grado base:
x^2 = a \implies x = \pm \sqrt{a}
E nel nostro caso:
x =\pm \sqrt{ y-1 }
Ora viene il terzo ed ultimo passaggio, nel quale dobbiamo trovare il dominio di questa nuova funzione (che si chiama codominio poiché c’è la y a destra, e da ora in poi chiameremo codominio e basta).
Abbiamo una funzione radice, per cui dobbiamo porre ciò che sta dentro la radice positiva o uguale a zero:
C: y-1 \ge 0 \implies y \ge 1
L’esercizio è concluso, nulla di impossibile, basta qualche altro esercizio svolto insieme.
Esercizio 2. Calcola il codominio di y = \frac{2x-1}{x+3}
Partiamo sempre dal dominio (non dimentichiamocene). Qui abbiamo una funzione fratta, di cui il suo dominio è:
D: x + 3 \ne 0 \implies x \ne -3
Passiamo ora al secondo passaggio, che è quello in cui vi dovete allenare di più, poiché chi non ha dimestichezza verso le formule, non troverà questi passaggi facili. Qui come sempre il consiglio che vi diamo è che vi dovete sempre levare di torno le frazioni.
y(x+3) = 2x-1
yx+3y = 2x-1
Considerando la y come un numero (anche se non lo è) sembrerebbe una equazione di primo grado, sicuramente portiamo tutte le x allora a sinistra:
yx -2x = -1 -3y
Mettiamo in evidenza la x:
(y -2) x = -1 -3y
E dividiamo tutto per y-2, in tal modo abbiamo isolato la x da sola:
x = \frac{ -1 -3y }{ y-2 }
Abbiamo finito. Abbiamo ottenuto finalmente un qualcosa del genere x=…y…. Per cui dobbiamo trovare il codominio di questa funzione.
Ricordiamo ancora una volta che le regole di un dominio sono le stesse di un codominio. Qui abbiamo una funzione fratta, per cui sempre denominatore diverso da zero!!!
C: y -2 \ne 0 \implies y \ne 2
I giochi son fatti.
Esercizio 3. Determina il codominio della funzione y = e^{-x} +1
Partiamo dal dominio, poiché alcuni professori segnano errore (perciò ve lo dico). Qui abbiamo una funzione esponenziale, e che non ha problemi di dominio. Essa è definita in tutto l’asse reale.
D: x \in \Reals
Trovare ora x(y) è veloce, ma serve che vi ricordiate una determinata formula. Per fortuna che ci sono questi esercizi svolti, così che possiate segnarvi sul foglio questa utilissima formula.
Portiamo prima l’esponenziale a sinistra da solo:
- e^{-x} = 1-y
Cambiamo di segno:
e^{-x} = y-1
A questo punto, dovreste ricordarvi una formula di questo tipo, che serviva a risolvere le equazioni esponenziali e logaritmiche.
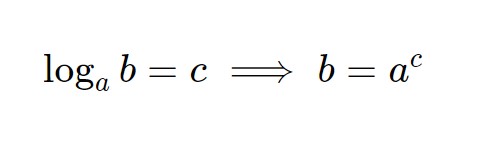
Questa ci permette di passare dall’esponenziale ad un logaritmo. Vediamo il membro di sinistra, e avremo:
-x = \ln (y-1)
Cambiamo di segno, ed otteniamo finalmente una x solitaria!
x = - \ln (y-1)
Ora non ci resta che trovare il suo coDOMINIO. Sopra di noi c’è un logaritmo. Se ci ricordiamo nella tabella dei domini, la funzione esiste se ciò che sta dentro è maggiore di zero:
C: y-1 >0 \implies y>1
Esercizio 4. Ricerca il codominio di y = \ln (2-x)
Partiamo dal dominio, abbiamo un logaritmo, di cui sappiamo che il suo dominio è:
D: 2-x > 0 \implies x<2
Fatto ciò passiamo al trasformare la nostra funzione, in ciò che vogliamo noi: la x a sinistra. Anche questa volta usiamo la stessa formula di prima, all’inverso però. RICORDATE: ogni volta che avete logaritmo oppure esponenziale si usa quella formula, in questo tipo di esercizi!
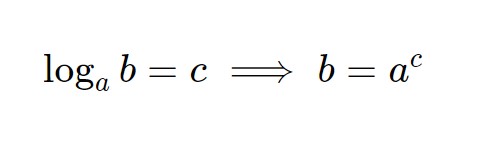
Nel nostro caso avremo di conseguenza:
2-x = e^y
RICORDA: il logaritmo naturale è un logaritmo in base “e”!
Ora è facile isolare la x, basta un immediato passaggio:
-x = e^y -2
x = -e^y +2
Ora che abbiamo ottenuto x(y), dobbiamo trovare il suo codominio. A destra abbiamo solo una funzione esponenziale che non ha problemi. Per cui:
C: y \in \Reals
Esercizio 5. Trova l’immagine di y = 1 - \sin \frac{1}{x}
Dominio per prima cosa. Qui abbiamo una funzione seno, e poi una funzione fratta. La funzione seno è definita in tutto R e quindi non ci sono problemi. Ci dobbiamo solo soffermare su quella fratta, per cui:
D: x \ne 0
Fatto ciò andiamo col secondo passaggio. Abbiamo già detto che al Liceo immagine=codominio, per cui non cambia nulla nell’esercizio. Ogni volta che abbiamo un seno o coseno, dobbiamo agire in un modo un po’ diverso. Come di solito però, isoliamo a sinistra la funzione con la x:
\sin \frac{1}{x} = 1-y
A questo punto, visto che il seno non lo possiamo levare all’improvviso dividendo o facendo qualcos’altro. In questo caso la x sta DENTRO una funzione (il seno). La cacciamo fuori con la sua funzione inversa.
\sin a = b \implies a = \arcsin b
Per noi:
\sin \frac{1}{x} = 1-y \implies \frac{1}{x} = \arcsin (1-y)
A questo punto abbiamo sì la x a sinistra, ma sta al denominatore. Invertiamo proprio tutto in un solo passaggio:
x = \frac{1}{\arcsin (1-y)}
Abbiamo finito il secondo passaggio, è stata dura e complicata (ma con il seno e coseno sono poi sempre gli stessi passaggi).
Calcoliamo il codominio di questa funzione. Commentiamola: abbiamo una funzione fratta (denominatore diverso da zero) e poi una funzione arcseno (argomento fra -1 ed 1). Essendo più codomini da considerare, vanno messi a sistema:
C: \begin{cases} -1 \le 1-y \le 1 \\ \arcsin (1-y) \ne 0 \end{cases}
La prima disequazione la risolviamo facilmente, sottraendo tutti e 3 i termini per -1:
C: \begin{cases} -2 \le -y \le 0 \\ \arcsin (1-y) \ne 0 \end{cases}
E poi cambiamo di segno il primo rigo (nelle disequazioni si cambia anche il segno del maggiore e minore):
C: \begin{cases} 0 \ge y \ge 2 \\ \arcsin (1-y) \ne 0 \end{cases}
Poi ci rimane il secondo rigo del sistema da risolvere.
\arcsin (1-y) \ne 0 \implies 1-y \ne 0 \implies y \ne 1
Per cui:
C: \begin{cases} 0 \ge y \ge 2 \\ y \ne 1 \end{cases}
Il sistema lo si risolve prendendo gli intervalli che sono in comune.
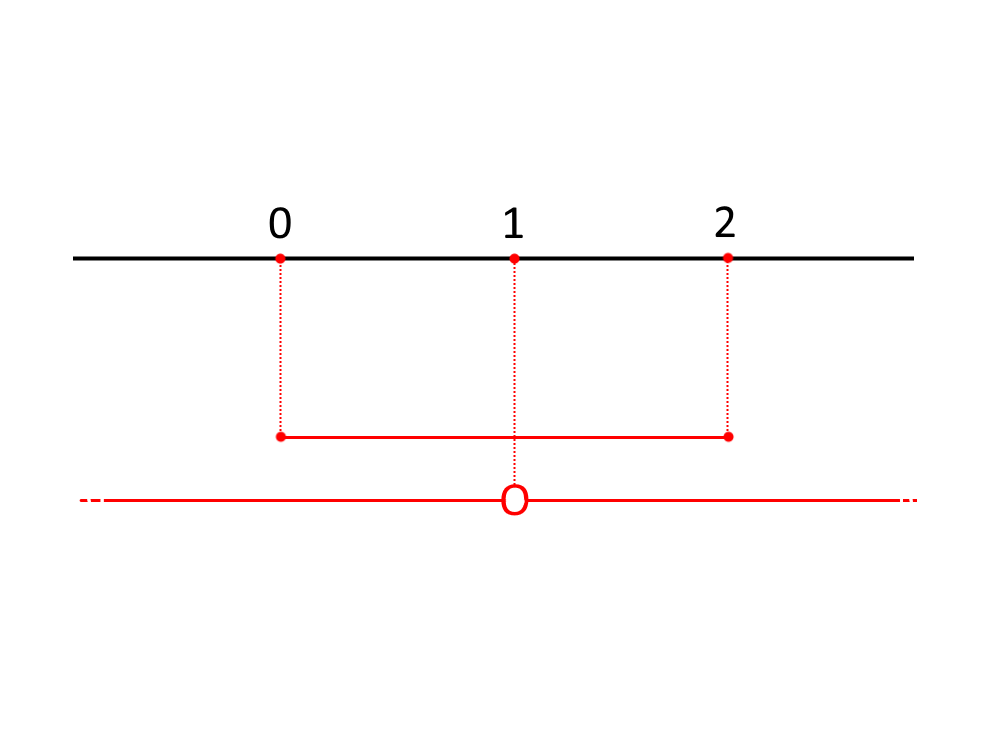
Per cui la soluzione finale sarà:
C: 0 \ge y \ge 2 \land y \ne 1
La pagina è conclusa. In questa abbiamo visto un argomento tanto discusso e tanto dubbioso, quello del codominio. Speriamo di avervi chiarito un pochetto in più le idee, e se avete domande o dubbi ricordate che potete contattarci per email. Vi risponderemo in men che non si dica!
dominio
del segno