Esercizi Equazioni Esponenziali
ESERCIZI Equazioni Esponenziali ! Ben 15 esercizi spiegati passo dopo passo e con calma; vi faremo vedere tutti i metodi che servono per risolvere le equazioni esponenziali: sarete pronti per la verifica! In questa pagina sarà necessario conoscere le basi delle equazioni di secondo grado. Ma non perdiamoci in chiacchiere ed iniziamo subito!
Indice
- Proprietà potenze
- Equazioni esponenziali con basi uguali
- Equazioni esponenziali con basi diverse
- Equazioni esponenziali con sostituzione
Vediamo prima di iniziare, alcune proprietà che ci serviranno: segnatevele!
Proprietà potenze

Iniziamo subito con gli esercizi equazioni esponenziali!
Esercizi equazioni esponenziali con basi uguali
Sintetizziamo i punti principali che dobbiamo andare a seguire per risolvere queste equazioni esponenziali.

Esercizio 1. 2^x = 16 \cdotp \sqrt{2}
Alcune equazioni esponenziali, come questa, posseggono tutti termini con stessa base: in questo caso base 2. Il trucco per la risoluzione di questi è riscrivere tutta l’equazione utilizzando le proprietà delle potenze per avere tutti 2 come base. Questo è il PRIMO PASSAGGIO.
A primo membro abbiamo già una base 2, passiamo quindi al secondo membro dell’equazione. Notiamo che abbiamo un 16, esso può essere scritto come:
16=2 \cdotp 2 \cdotp 2 \cdotp 2 = 2^4
Poi ci rimane la radice, per questo utilizziamo la settima proprietà delle potenze:
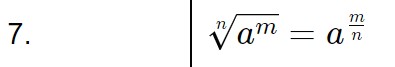
Quindi nel nostro caso la radice di 2 può essere scritta come:
\sqrt{2} = 2^{\frac{1}{2}}
Ricordatevi che la radice senza sopra scritto nulla significa radice seconda. L’equazione può essere riscritta quindi come:
2^x = 2^4 \cdotp 2^{\frac{1}{2}}
Adesso avviene il SECONDO PASSAGGIO: dobbiamo avere una sola base a sinistra ed una sola base a destra. Al secondo membro quindi facciamo la moltiplicazione fra quelle due potenze sfruttando la prima proprietà delle potenze:
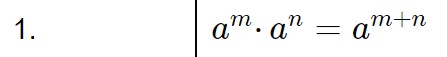
Quindi:
2^x = 2^{4 + \frac{1}{2} }
Facciamo il minimo comune multiplo solo sopra l’esponente:
2^x = 2^{ \frac{8+1}{2} }
2^x = 2^{ \frac{9}{2} }
Ora che abbiamo due basi uguali a sinistra e destra, avviene l’ULTIMO PASSAGGIO: visto che le basi sono uguali e visto che c’è una uguaglianza fra loro, allora significa che anche gli esponenti sono uguali, e quindi mettiamo in uguaglianza solo gli esponenti:
x = \frac{9}{2}
Ed abbiamo così trovato la x!
Volendo, durante la verifica in classe visto che non avete il risultato del libro, per vedere se avete commesso errori potete effettuare la verifica dell’equazione, per controllare se le soluzioni sono giuste.
Esercizio 3. 3^x = \frac{9 \sqrt{3} }{\sqrt[4]{3} }
Seguiamo sempre gli stessi punti. Facciamo una cosa alla volta. Scriviamo innanzitutto:
9=3^2
E la radice al numeratore che abbiamo già visto:
\sqrt{3}=3^{ \frac{1}{2} }
Abbiamo ora una radice con indice 4 a denominatore. Per questo sfruttiamo la settima proprietà delle potenze.
Quindi nel nostro caso:
\sqrt[4]{3} =3^{ \frac{1}{4} }
Il 4 prende il posto al denominatore nell’esponente in pratica.
Sostituiamo tutto:
3^x = \frac{3^2 3^{ \frac{1}{2} } }{3^{ \frac{1}{4} } }
Ora piuttosto che portare il denominatore sopra, possiamo anche direttamente sfruttare la seconda proprietà delle potenze:
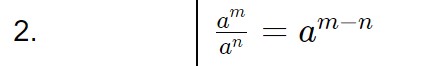
E quindi segue che andiamo a sommare gli esponenti che stanno al numeratore ed andiamo a sottrarre quello che sta al denominatore:
3^x = 3^{2 + \frac{1}{2} - \frac{1}{4} }
Facciamo il minimo comune multiplo all’esponente adesso.
3^x = 3^{2 + \frac{1}{2} - \frac{1}{4} }
3^x = 3^{ \frac{8+2-1}{4} }
E quindi:
3^x = 3^{ \frac{9}{4} }
E mettiamo gli esponenti in uguaglianza.
x = \frac{9}{4}
CI SONO ABBASTANZA PROPRIETA’, MA DOPO UN POCO LE AVRETE IMPARATE, NON VI PREOCCUPATE, I PASSAGGI SONO SEMPRE GLI STESSI.
Continuiamo con altri esercizi equazioni esponenziali svolte!
Esercizio 4. 8^x \cdotp \sqrt{2}= 4^x
Iniziamo a vedere come trattare il termine 8^x.
8^x = (8)^x = (2^3)^x
Ed a questo punto usiamo la terza proprietà delle potenze.
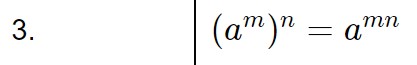
E quindi ciò che succede è che abbiamo che il 3 e la x si moltiplicano dando vita a 3x.
8^x = 2^{3x}
Discorso analogo per il termine seguente:
4^x = 2^{2x}
Mentre la radice già l’abbiamo discussa e riportiamo solo il risultato:
\sqrt{2}= 2^{ \frac{1}{2} }
Sostituiamo tutti questi risultati nell’equazione iniziale dell’esercizio.
2^{3x} \cdotp 2^{ \frac{1}{2} }= 2^{2x}
Svolgiamo la moltiplicazione solo a primo membro, per ottenere così un’unica base:
2^{3x + \frac{1}{2} }= 2^{2x}
E mettiamo direttamente in uguaglianza i membri senza fare il mcm che è più conveniente in questo caso. Ci viene una equazione:
3x + \frac{1}{2} = 2x
A differenza degli altri esercizi, qui è uscita fuori una equazione di primo grado vera e propria, quindi risolviamola! Portiamo le x da una parte e il termine noto dall’altra!
3x -2x = - \frac{1}{2}
x = - \frac{1}{2}
Continuiamo con altri esercizi equazioni esponenziali svolte!
Esercizio 5. 4^{ 2x+1 } = 8^{ 2x-1 }
Trattiamo il primo termine facendo vedere tutti i passaggi:
4^{ 2x+1 } = (4)^{ 2x+1 } = (2^2)^{ 2x+1 }
E come prima, usiamo la stessa proprietà, e moltiplichiamo quindi gli esponenti fra di loro:
4^{ 2x+1 } = (2^2)^{ 2x+1 } = 2^{2(2x+1)}
= 2^{4x + 2}
dove abbiamo svolto la parentesi semplicemente. Facciamo lo stesso discorso per il secondo termine, questa volta provateci voi e poi venite a vedere la soluzione!
8^{ 2x-1 } = (8)^{ 2x-1 } = (2^3)^{2x-1} =
=2^{ 3(2x-1) } = 2^{ 6x - 3 }
Sostituiamo i rispettivi termini trovati nell’equazione!
2^{4x + 2} = 2^{ 6x - 3 }
Ciò l’abbiamo fatto per ricondurci ad una stessa base ovviamente, non dimenticatevelo! Adesso uguagliamo gli esponenti come sempre:
4x + 2 = 6x - 3
Abbiamo ancora una volta una equazione di primo grado, svolgiamola per trovare la x.
4x - 6x = - 3 -2
- 2x = - 5
Cambiamo tutto di segno e dividiamo per 2, otteniamo la soluzione dell’esercizio:
x=\frac{5}{2}
Esercizio 6. 7^x = 1
Questo è un esercizio utile perchè può tornare in diversi esercizi. Qui il trucchetto è semplicemente scrivere quell’1 come:
1=7^0
E quindi l’1 non rappresenta mai un problema perchè può essere ricondotto a qualsiasi base!
7^x = 7^0
\implies x=0
Continuiamo con altri diversi esercizi equazioni esponenziali!
Equazioni esponenziali con basi diverse
Esercizio 7. 4^{ x+1 } + 3^x = 0
Allora partiamo col dire che questo sicuramente è la tipologia di esercizio più difficile degli esponenziali. Quindi se non riuscite a capire per il momento andate avanti e poi tornate un’altra volta qui.
Il trucco alla base di questi tipi di equazioni esponenziali senza base comune è quello di dividere tutta l’equazione per uno dei termini esponenziali. Ad esempio in questo caso se dividiamo per 3^x segue che:
\frac{4^{ x+1 } }{3^x} + \frac{3^x}{3^x} = 0
\frac{4^{ x+1 } }{3^x} + 1 = 0
Sciogliamo il termine al numeratore sfruttando al contrario la prima proprietà delle potenze (cioè leggendo la formula da destra a sinistra).
\frac{4^x \cdotp 4^1 }{3^x} + 1 = 0
\frac{4^x \cdotp 4 }{3^x} + 1 = 0
Mettiamo il 4 davanti alla frazione.
4 \frac{4^x }{3^x} + 1 = 0
Ora sfruttiamo la sesta proprietà delle potenze, ossia quella in cui abbiamo non la stessa base ma stesso esponente!
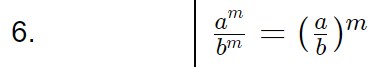
Segue che:
4 (\frac{4}{3})^x + 1 = 0
Ora portiamo l’1 a secondo membro:
4 (\frac{4}{3})^x = -1
E dividiamo per 4:
(\frac{4}{3})^x = - \frac{1}{4}
Abbiamo che un termine esponenziale è uguale ad un numero negativo, ma ciò è impossibile perchè un esponenziale per definizione è sempre positivo. Quindi questa equazione non ha soluzione.
Continuiamo con altri esercizi equazioni esponenziali!
Esercizio 8. 6 \cdotp 2^{ x+3 } = 4 \cdotp 7^x - 2^x
Quindi in queste equazioni piuttosto che stessa base il trucco sta NEL RICONDURRE TUTTO AD UNO STESSO ESPONENTE.
Qui sciogliamo solamente il 2^{x+3} applicando al contrario la prima proprietà delle potenze ed otteniamo già uno stesso esponente:
6 \cdotp 2^x \cdotp 2^3 = 4 \cdotp 7^x - 2^x
6 \cdotp 2^3 \cdotp 2^x = 4 \cdotp 7^x - 2^x
Moltiplico il 6 con il 2^3, cosa che posso fare tranquillamente.
48 \cdotp 2^x = 4 \cdotp 7^x - 2^x
E poi porto il 2^x a primo membro, in modo che i due si possano sommare:
48 \cdotp 2^x + 2^x= 4 \cdotp 7^x
49 \cdotp 2^x = 4 \cdotp 7^x
Due esponenziali uguali si possono sommare, sommando i coefficienti relativi. Ad esempio per capire meglio posso sommare:
3 \cdotp a^x + 2 \cdotp a^x = 5 \cdotp a^x
Torniamo al nostro esercizio. Ora quello che dobbiamo fare è dividere per uno dei due termini esponenziali, ad esempio dividiamo tutto per 7^x:
49 \frac{2^x}{7^x} = 4 \frac{7^x}{7^x}
49 \frac{2^x}{7^x} = 4
Ed ora dividiamo per 49 in modo da isolare il termine esponenziale:
\frac{2^x}{7^x} = \frac{4}{49}
Applichiamo la sesta proprietà delle potenze, avendo uno stesso esponente.
(\frac{2}{7})^x = \frac{4}{49}
A questo punto notiamo che possiamo riscrivere anche il secondo membro come:
(\frac{2}{7})^x = \frac{2^2}{7^2}
Ed applichiamo la medesima proprietà.
(\frac{2}{7})^x = (\frac{2}{7})^2
Siamo arrivati al primo caso: cioè stessa base da ambo le parti. Quindi uguagliamo gli esponenti ed il gioco è fatto!
x =2
Continuiamo con degli esercizi equazioni esponenziali con sostituzione!
Esercizi equazioni esponenziali
con sostituzione
Esercizio 9. 4^x = 2^x - 2
Il primo passo per questo tipo di equazioni è quello di ricondurci prima di tutto ad una stessa base per i termini esponenziali, gli altri numeri possono rimanere così come sono. Quindi riscriviamo solo il primo termine come:
4^x = (4)^x = (2^2)^x = 2^{2x}
Sostituiamo questo dato nell’equazione dell’esercizio.
2^{2x} = 2^x - 2
A questo punto che abbiamo i termini esponenziali con stessa base procediamo per sostituzione. Poniamo:
2^x = z
E quindi:
z^2 = z - 2
In pratica ci siamo ricondotti ad una semplice equazione di secondo grado. Se non avete capito perchè esce fuori z^2 ve lo spiego meglio passo per passo:
2^{2x} = (2^x)^2 = (z)^2 =z^2
Torniamo all’esercizio. Riordiniamo nella classica forma l’equazione di secondo grado:
z^2 - z + 2 = 0
E la risolviamo con il solito procedimento: calcoliamo prima di tutto il discriminante. (se non ricordate questi passaggi andateveli un attimino a vedere cliccando qui).
\Delta = b^2 - 4ac = 1 - 8 = -7<0
Visto che il Delta<0 non esiste soluzione all’equazione, e quindi l’equazione iniziale è impossibile.
Esercizio 10. 8 + 2^{ x+1 } = 2^{ 2x }
Primo passo: ricondurre solo i termini esponenziali ad una stessa base per questo tipo di equazioni. Qui già ce l’abbiamo, scriviamo allora semplicemente per una forma migliore e per poi poter sostituire senza problemi:
8 + 2^x \cdotp 2 = 2^{ 2x }
Ed ora siamo nelle condizioni per poter sostituire il termine esponenziale. Poniamo:
z=2^x
Sostituendo nell’equazione risulta:
8 + 2z = z^2
Riordiniamo ad una forma migliore l’equazione di secondo grado per poi poter calcolare il discriminante.
z^2 -2z - 8 = 0
Calcoliamo il discriminante, utilizzando la formula per il coefficiente b pari:
\frac{\Delta}{4} = (\frac{b}{2})^2 - ac = 1 + 8 = 9
Il delta>0 e quindi ci aspettiamo due soluzioni distinte e separate, andiamocele a calcolare utilizzando la formula:
z_{1,2}= \frac{-\frac{b}{2} \pm \sqrt{\frac{\Delta}{4}} }{a} = \frac{1 \pm 3}{1}
E quindi le due soluzioni sono:
z_1 = \frac{1 + 3}{1} = 4
z_2 = \frac{1 - 3}{1} = -2
L’esercizio attenzione perchè non è concluso! Queste sono le soluzioni nella variabile z, ora dobbiamo ripassare alla variabile x! E quindi risostituiamo.
z=2^x
Partiamo dalla prima soluzione:
4=2^x
Riconduciamo tutto ad una stessa base:
2^2=2^x
Ed abbiamo una semplice equazione esponenziale del primo tipo che abbiamo visto all’inizio di questa pagina. Essendo stessa base a destra e sinistra mettiamo in uguaglianza gli esponenti, quindi:
x=2
Adesso passiamo all’altra soluzione z= -2:
z=2^x
-2 =2^x
Ricordiamo sempre che un esponenziale è per definizione sempre positivo (non la x ma proprio tutto l’esponenziale) e quindi non può essere uguale a -2: qui non c’è soluzione.
L’unica soluzione che prendiamo è quella di prima e cioè x=2.
Continuiamo con altri esercizi equazioni esponenziali svolte!
Esercizio 11. 9^x -3 = 2 \cdotp 3^x
Primo passo come sempre: ricondurci ad una stessa base qualora fosse possibile. Quindi riscriviamo solo:
9^x = (3^2)^x = 3^{2x}
Ed ora la nostra equazione esponenziale ci piace:
3^{2x} - 3 = 2 \cdotp 3^x
A questo punto possiamo procedere per sostituzione. Poniamo:
3^x = z
E quindi la nostra equazione diventa:
z^2 - 3 = 2z
Ossia una equazione di secondo grado, riordiniamola un attimo:
z^2 -2z - 3 = 0
Ora che la nostra forma va bene, calcoliamo il discriminante ( o delta sono sinonimi ) per coefficiente b pari :
\frac{\Delta}{4} = (\frac{b}{2})^2 - ac = 1 + 3 = 4
Il delta>0 quindi esistono due soluzioni, calcoliamole:
z_{1,2}= \frac{-\frac{b}{2} \pm \sqrt{\frac{\Delta}{4}} }{a} = \frac{1 \pm 2}{1}
E quindi le due soluzioni sono:
z_1 = \frac{1 + 2}{1} = 3
z_2 = \frac{1 - 2}{1} = -1
La seconda opzione la scartiamo di già per il discorso fatto in precedenza, cioè un esponenziale non può essere negativo e quindi:
3^x = z \implies 3^x = -1
non avrebbe soluzione. Pensiamo solo alla prima z=3:
3^x = z \implies 3^x = 3
3^x = 3^1
Stessa base, quindi uguaglianza degli esponenti ed allora l’unica soluzione è x=1!
Esercizio 12. 5^{ 2x } - 5^x = 5^{ x-2 } - \frac{1}{25}
I termini a primo membro ci stanno bene, mentre 5^{ x-2 } merita di essere un attimo scomposto meglio, altrimenti non si può fare la sostituzione. Usiamo la seconda proprietà delle potenze.
5^{ x-2 } = \frac{5^x}{5^2} = \frac{5^x}{25}
L’equazione ora è pronta per effettuare una sostituzione.
5^{ 2x } - 5^x = \frac{5^x}{25} - \frac{1}{25}
Poniamo:
z= 5^x
E quindi l’equazione diventa sempre una equazione di secondo grado:
z^2 - z = \frac{z}{25} - \frac{1}{25}
Per comodità moltiplichiamo tutto per 25 così ci leviamo da mezzo tutte le frazioni.
25z^2 - 25z = z - 1
25z^2 - 25z -z +1 = 0
E come al solito abbiamo una equazione di secondo grado ( possono anche uscire altri tipi di equazione ):
25z^2 - 26z +1 = 0
Calcoliamo il discriminante, usando la formula del coefficiente b pari:
\frac{\Delta}{4} = (\frac{b}{2})^2 - ac = 169 - 25 = 144
Discriminante>0, quindi le soluzioni esistono, andiamo a calcolarle:
z_{1,2}= \frac{-\frac{b}{2} \pm \sqrt{\frac{\Delta}{4}} }{a} = \frac{13 \pm 12}{25}
E quindi le due soluzioni sono:
z_1 = \frac{13 + 12}{25} = 1
z_2 = \frac{13 - 12}{25} = \frac{1}{25}
Partiamo dalla prima soluzione, ritornando alla variabile x iniziale, risostituendo:
z= 5^x
1= 5^x
L’1 come visto precedentemente in uno degli esercizi, si può scrivere come:
5^0= 5^x
Quindi la prima soluzione uguagliando gli esponenti, visto che è stessa base, è:
x=0
Calcoliamo l’altra:
\frac{1}{25}= 5^x
\frac{1}{5^2}= 5^x
Che riscriviamo come:
5^{-2}= 5^x
E quindi x=-2 è l’altra. In sintesi:
x=-2 \lor x=0
Continuiamo con altri esercizi equazioni esponenziali svolte!
Esercizio 13. 3^x + 3^{ 1-x } = 4
Iniziamo a scomporre, per rendere possibile la sostituzione, il secondo termine, applicando le solite proprietà delle potenze.
3^{ 1-x } = 3 \cdotp 3^{-x} = 3 \cdotp (3^x)^{-1}
E quindi:
3^x + 3 \cdotp (3^x)^{-1} = 4
Ora possiamo continuare, poniamo:
z=3^x
La nostra equazione diventa:
z + 3 \cdotp z^{-1} = 4
z + 3 \frac{1}{z} = 4
Abbiamo una equazione fratta, quindi prima di fare qualsiasi cosa bisogna prima scrivere le condizioni di esistenza, ossia denominatore diverso da zero.
CE: z \ne 0 \implies 3^x \ne 0
Ma questo è sempre diverso da zero, perchè l’esponenziale è definito positivo, ossia >0 (un’esponenziale non è mai negativo nè uguale a zero).
Ritornando all’equazione, è possibile risolverla in due modi equivalenti: o moltiplicando tutto per z o facendo il minimo comune multiplo. Noi scegliamo ad esempio di moltiplicare già tutto per z. In tal modo viene fuori una equazione di secondo grado.
z^2 + 3 = 4z
z^2 -4z + 3 = 0
Calcoliamo il delta-quarti:
\frac{\Delta}{4} = (\frac{b}{2})^2 - ac = 4 - 3 = 1
Discriminante>0: calcoliamo le due soluzioni in variabile z:
z_{1,2}= \frac{-\frac{b}{2} \pm \sqrt{\frac{\Delta}{4}} }{a} = \frac{2 \pm 1}{1}
E quindi le due soluzioni sono:
z_1 = 2+1=3
z_2 = 2-1 = 1
Ritorniamo alla variabile x iniziale, risostituiamo mettendoci la prima soluzione z=3:
3^x = 3 \implies x = 1
E poi l’altra:
3^x = 1 \implies 3^x = 3^0 \implies x = 0
Continuiamo con altri esercizi equazioni esponenziali svolte!
Esercizio 14. (\frac{1}{2})^{2x} - \frac{12}{2^x} + 32 = 0
Questa può sembrare difficile a prima vista, in realtà è solo molto “disordinata”. Riscriviamo il primo termine in una forma più umana e risolvibile:
\frac{1}{2^{2x} } - \frac{12}{2^x} + 32 = 0
Passiamo a sostituire:
z=2^x
\frac{1}{z^2 } - \frac{12}{z} + 32 = 0
Abbiamo una equazione fratta sicuramente, quindi andiamo a fare le condizioni di esistenza.
CE: z\ne 0 \implies z \ne 0
Procediamo come sempre per quanto riguarda le equazioni fratte, col mcm.
\frac{1 - 12z + 32z^2}{z^2 } = 0
E poi semplifichiamo il denominatore.
1 - 12z + 32z^2 = 0
Cioè una equazione di secondo grado ancora!
32z^2 -12z +1= 0
Calcoliamo il delta-quarti:
\frac{\Delta}{4} = (\frac{b}{2})^2 - ac = 36 - 32 = 4
Discriminante>0: calcoliamo le due soluzioni in variabile z:
z_{1,2}= \frac{-\frac{b}{2} \pm \sqrt{\frac{\Delta}{4}} }{a} = \frac{6 \pm 2}{32}
E quindi le due soluzioni sono:
z_1 = \frac{6 + 2}{32}= \frac{1}{4}
z_2 = \frac{6 - 2}{32} = \frac{1}{8}
Entrambe rispettano le CE, quindi non ne scartiamo nessuna. Risostituiamo:
2^x = \frac{1}{4}
2^x = 2^{-2} \implies x=-2
E l’altra:
2^x = \frac{1}{8}
2^x = 2^{-3} \implies x=-3
E l’esercizio è concluso!
Esercizio 15. \frac{4}{2^x - 1} + \frac{3}{2^x +1 } = 5
Possiamo passare direttamente alla sostituzione.
z= 2^x
\frac{4}{z - 1} + \frac{3}{z +1 } = 5
Abbiamo un’altra volta una equazione fratta (cliccateci sopra per ripeterle un attimino). Prima di mettere mano alla risoluzione, calcoliamo le condizioni di esistenza delle due frazioni.
CE: z-1 \ne 0 \implies z \ne 1
CE: z+1 \ne 0 \implies z \ne -1
Ora possiamo svolgerla. Nelle equazioni fratta il primo punto è fare il minimo comune multiplo ad ambo i membri.
\frac{ 4(z+1) + 3(z-1) }{(z - 1)(z+1)} = \frac{5(z - 1)(z+1)}{(z - 1)(z+1)}
Poi semplifichiamo i denominatori:
4(z+1) + 3(z-1) = 5(z - 1)(z+1)
Per il secondo termine sfruttiamo la seguente regola algebrica della differenza di quadrati per risolverla più velocemente:
a^2 - b^2 = (a-b)(a+b)
Ed allora:
4z+4 + 3z-3 = 5( z^2 -1 )
4z+4 + 3z-3 = 5z^2 -5
Sommiamo i termini simili e portiamo tutto a primo membro:
5z^2 -7z - 6 = 0
Abbiamo una equazione di secondo grado, calcoliamo il delta:
\Delta = b^2 - 4ac = 49 + 120 = 169
E le due conseguenti soluzioni sono:
z_{1,2}= \frac{-b \pm \sqrt{\Delta} }{2a} = \frac{7 \pm 13}{10}
z_1 = \frac{7 + 13}{10} = 2
z_2 = \frac{7 - 13}{10} = - \frac{6}{10}
Entrambe rispettando le CE.
La seconda la scartiamo perchè è negativa ed un esponenziale non può essere negativo.
La prima invece risostituiamo:
2^x = 2 \implies x=1
In questa pagina abbiamo visto come svolgere degli esercizi sulle equazioni esponenziali, applicando vari metodi compreso quello per sostituzione. Potete continuare ad esercitarvi su questo sito con altre centinaia di esercizi di tutti i tipi sia di matematica che di geometria analitica e geometria!
Altro argomento importante per questa pagina sono state le equazioni chiaramente, le equazioni di secondo grado e le equazioni fratte, vi consiglio di ripeterle o vedere giusto un po’ le formule ed i passaggi.
Per approfondire:
https://it.wikipedia.org/wiki/Equazione_esponenziale
Esercizi equazioni esponenziali.
composta
esponenziali