Equazioni irrazionali ESERCIZI
Equazioni irrazionali ESERCIZI: 15 esercizi SVOLTI! Lo svolgimento delle equazioni irrazionali ruota attorno ad una sola formula ed alle condizioni di esistenza. Ci sono però diverse applicazioni che tale formula può avere: in questa pagina le vedremo tutte, spiegate passo dopo passo e con calma! Iniziamo subito!
Indice
- Formule per le equazioni irrazionali
- Equazioni irrazionali \sqrt{ A(x) } = k
- Equazioni irrazionali \sqrt{ A(x) } = B(x)
- Equazioni irrazionali con due radicali
Iniziamo subito a vedere le due formule molto simili che andremo ad utilizzare in diversi casi in questa pagina!
Formule per le equazioni irrazionali

Iniziamo subito con le equazioni irrazionali esercizi svolti!
Equazioni irrazionali esercizi
\sqrt{ A(x) } = k
Esercizio 1. \sqrt{x-3} = 5
Come primissima cosa in qualsiasi equazione e disequazione bisogna scrivere le condizioni di esistenza: importantissime perché ci permetteranno di dire alla fine dell’esercizio se la soluzione trovata è da scartare o da tenere.
Le condizioni di esistenza di una radice (con indice pari) consiste nel porre il radicando (cioè quello che c’è dentro) maggiore o uguale a zero. Quando non vedete nessun indice sopra la radice significa che è 2. In questo esercizio l’indice è quindi 2 e perciò bisogna fare le CE.
Nel nostro caso:
CE: x-3 \ge 0 \implies x \ge 3
Quindi la soluzione finale dovrà essere maggiore o uguale di 3. Ora passiamo alla risoluzione dell’esercizio vera e propria. Vedendo nelle formule, applichiamo la prima, con radice pari.
Dobbiamo quindi risolvere il seguente sistema:
\begin{cases} 5 \ge 0 \\ x-3 = 5^2 \end{cases}
\begin{cases} 5 \ge 0 \\ x-3 = 25 \end{cases}
Il primo termine del sistema è un 5 che è ovviamente sempre maggiore o uguale di zero indipendentemente dalla x, perché non c’è qui! Quindi scriviamo \forall x : cioè per qualsiasi x!
\begin{cases} \forall x \\ x-3 = 25 \end{cases}
Il secondo termine è una equazione lineare, che risolviamo semplicemente portando il -3 a secondo membro.
\begin{cases} \forall x \\ x = 28 \end{cases}
In un sistema si prendono le soluzioni comuni. Visto che il primo termine è per qualsiasi x, allora prendiamo proprio x=28!
Adesso c’è l’ultimo passaggio di ogni equazione o disequazione: verificare se la soluzione va bene con le CE. Per far ciò si mette a sistema le CE e la soluzione:
\begin{cases}x \ge 3 \\ x = 28 \end{cases}
Vedete chiaramente nello schema seguente che la soluzione va bene!
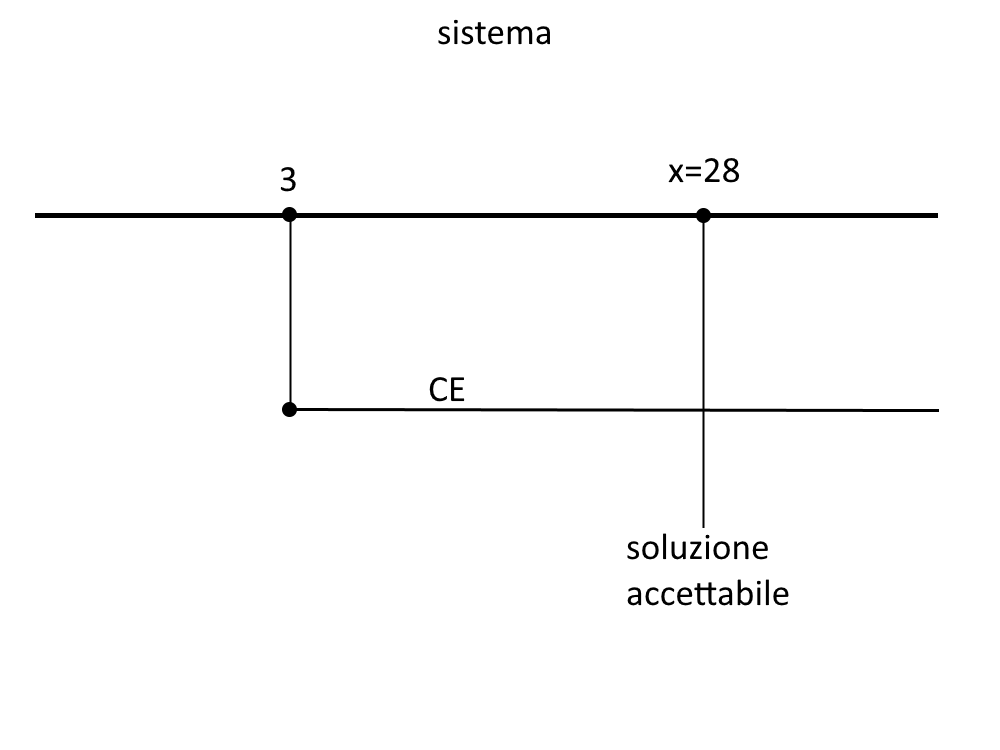
Volendo, durante la verifica in classe visto che non avete il risultato del libro, per vedere se avete commesso errori potete effettuare la verifica dell’equazione, per controllare se le soluzioni sono giuste.
Esercizio 2. \sqrt[3]{x+2} = 4
Qua abbiamo una equazione irrazionale con radice con indice dispari. Quando abbiamo un indice dispari le condizioni di esistenza NON si devono fare!
Passiamo direttamente allo svolgimento dell’esercizio: applichiamo la seconda formula, quella con indice dispari. Eleviamo quindi solamente alla terza tutto:
(\sqrt[3]{x+2})^3 = 4^3
x+2 = 64
Abbiamo una equazione normale, che risolviamo:
x = 64-2
x=62
Qui non ci sono le CE, e quindi la soluzione va bene.
Esercizio 3. \sqrt{3x-4} = -2
Abbiamo una radice con indice pari, quindi scriviamo le condizioni d’esistenza: cioè radicando maggiore o uguale di 0.
CE: 3x-4 \ge 0 \implies 3x \ge 4
\implies x \ge \frac{4}{3}
Passiamo all’esercizio. Adesso possiamo passare all’applicare la formula!
\begin{cases} -2 \ge 0 \\ (\sqrt{3x-4})^2 = (-2)^2 \end{cases}
Visto che il primo termine è negativo sempre, allora non esisterà nessuna x per la quale il -2 sia maggiore o uguale di 0! Questo primo termine in questi casi è importantissimo!
Quindi scriviamo:
\begin{cases} \nexists x \\ (\sqrt{3x-4})^2 = (-2)^2 \end{cases}
In un sistema si prendono le soluzioni in comune, ma visto che il primo termine mi dice per nessuna x, allora non c’è bisogno di fare altri calcoli perché non esisterà soluzione!
Continuiamo con altre equazioni irrazionali esercizi svolti!
Esercizio 4. \sqrt[3]{2x} = -2
Qui abbiamo una radice con indice dispari, per cui non dobbiamo scrivere alcuna CE per la radice. Passiamo direttamente all’applicare la formula per indice dispari!
( \sqrt[3]{2x})^3 = (-2)^3
A differenza di prima, un numero negativo non comporta problemi con indice dispari.
2x = -8
Divido tutto per 2:
x = -4
Esercizio 5. 3\sqrt[4]{5x} = 3
Abbiamo una radice con indice pari (4) e allora scriviamo innanzitutto le condizioni di esistenza.
CE: 5x \ge 0 \implies x \ge 0
Adesso passiamo all’esercizio. Non possiamo ancora applicare la formula perché non abbiamo a sinistra solamente una radice ma c’è anche un 3! Nella formula come vedete al primo membro c’è solo la radice. Quindi dividiamo tutto per 3:
\sqrt[4]{5x} = 1
Ora siamo nelle condizioni di applicare la formula! Risolviamo il sistema:
\begin{cases} 1 \ge 0 \\ 5x = 1^4 \end{cases}
\begin{cases} 1 \ge 0 \\ 5x = 1 \end{cases}
Il primo termine è ovviamente maggiore o uguale di zero, quindi scriviamo per ogni x! Il secondo dividiamo per 5:
\begin{cases} \forall x \\ x = \frac{1}{5} \end{cases}
La soluzione di questo sistema è quindi x = \frac{1}{5} .
Vediamo adesso se questa soluzione va bene o bisogna scartarla: mettiamola a sistema con le CE.
\begin{cases} x = \frac{1}{5} \\ x \ge 0 \end{cases}
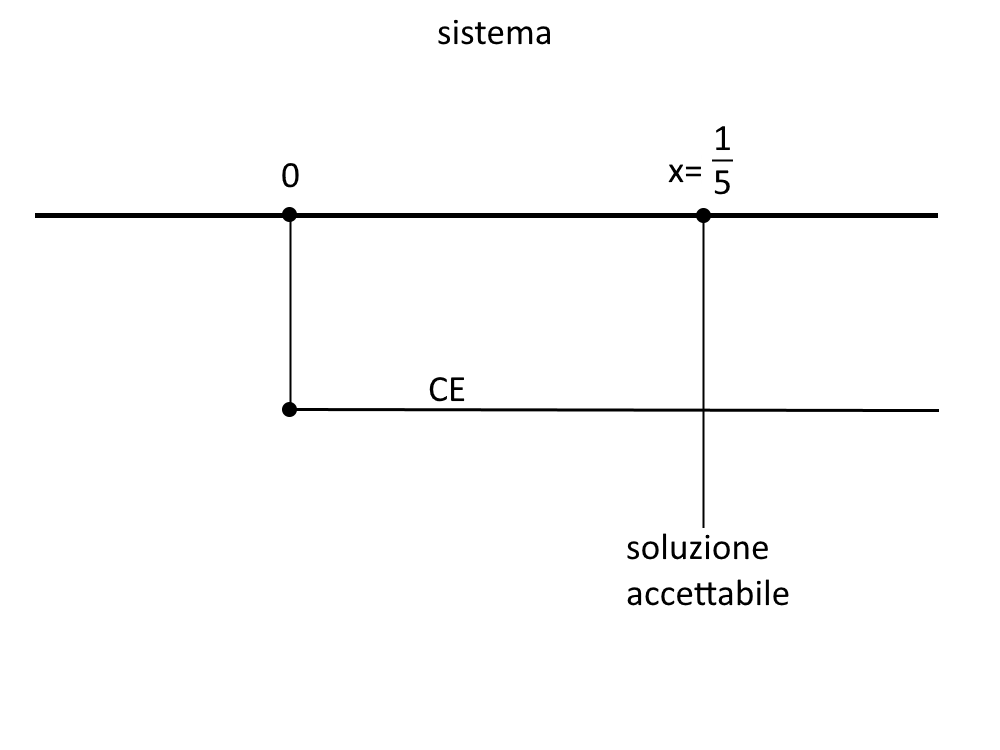
Continuiamo con altre equazioni irrazionali esercizi svolti!
Equazioni irrazionali esercizi
\sqrt{ A(x) } = B(x)
Esercizio 6. 1= 3x - \sqrt{ x+3 }
Abbiamo una radice con indice pari, scriviamo la sua condizione d’esistenza prima di tutto.
CE: x +3 \ge 0 \implies x \ge -3
Passiamo all’esercizio: dobbiamo arrivare alla forma della formula, ossia con una radice a sinistra e gli altri termini a destra. Portiamo la radice a primo membro, e l’1 al secondo.
\sqrt{ x+3 } = 3x - 1
Ora siamo nelle condizioni giuste. Applichiamo la formula e scriviamo il sistema. Nel nostro caso:
A(x)=x+3
B(x)=3x-1
Ed allora:
\begin{cases} 3x-1 \ge 0 \\ x+3 = (3x-1)^2 \end{cases}
A secondo termine abbiamo un quadrato di un binomio. Se non vi ricordate come si fanno eccovi:
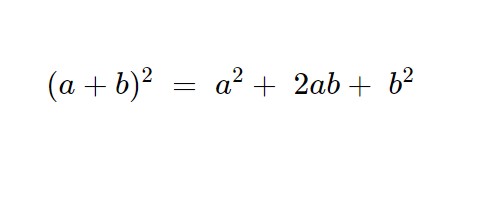
\begin{cases} 3x \ge 1 \\ x+3 = 9x^2 -6x +1\end{cases}
Abbiamo a secondo termine una equazione di secondo grado. Porto tutto da un lato quindi, in modo da poter poi calcolare il delta. Se non vi ricordate cliccateci sopra per le formule che comunque vi farò vedere.
\begin{cases} x \ge \frac{1}{3} \\ 9x^2 -6x +1 -x-3 =0\end{cases}
\begin{cases} x \ge \frac{1}{3} \\ 9x^2 -7x -2 =0\end{cases}
La prima disequazione è ok, calcoliamo quindi il discriminante della seconda equazione:
\Delta = b^2 -4ac = 49+72=121
Delta>0 e quindi esistono due soluzioni distinte. Calcoliamole:
x_{1,2} = \frac{-b \pm \sqrt{\Delta} }{2a} = \frac{7 \pm 11}{18}
E quindi le due soluzioni sono:
x_1 = \frac{7 + 11}{18} = 1
x_2 = \frac{7 - 11}{18} = - \frac{2}{9}
Adesso prima di concludere l’esercizio, dobbiamo verificare se queste soluzioni vanno bene. Mettiamole a sistema con le CE:
\begin{cases} x \ge -3 \\ x=1 \lor x=- \frac{2}{9} \end{cases}
E quindi prendiamo solamente x=1. L’altra la scartiamo!
Esercizio 7. \sqrt{ x^2 -9x } =5-x
CE: x^2 -9x \ge 0
Mettiamo in evidenza la x:
CE: x(x -9) \ge 0
E risolviamo questo con un falso sistema.
\big\| x \ge 0 \\ \big\| x-9 \ge 0
\big\| x \ge 0 \\ \big\| x \ge 9
Facciamo ora un quadro dei segni, e prendiamo le parti col segno + visto che la disequazione è con un maggiore o uguale.
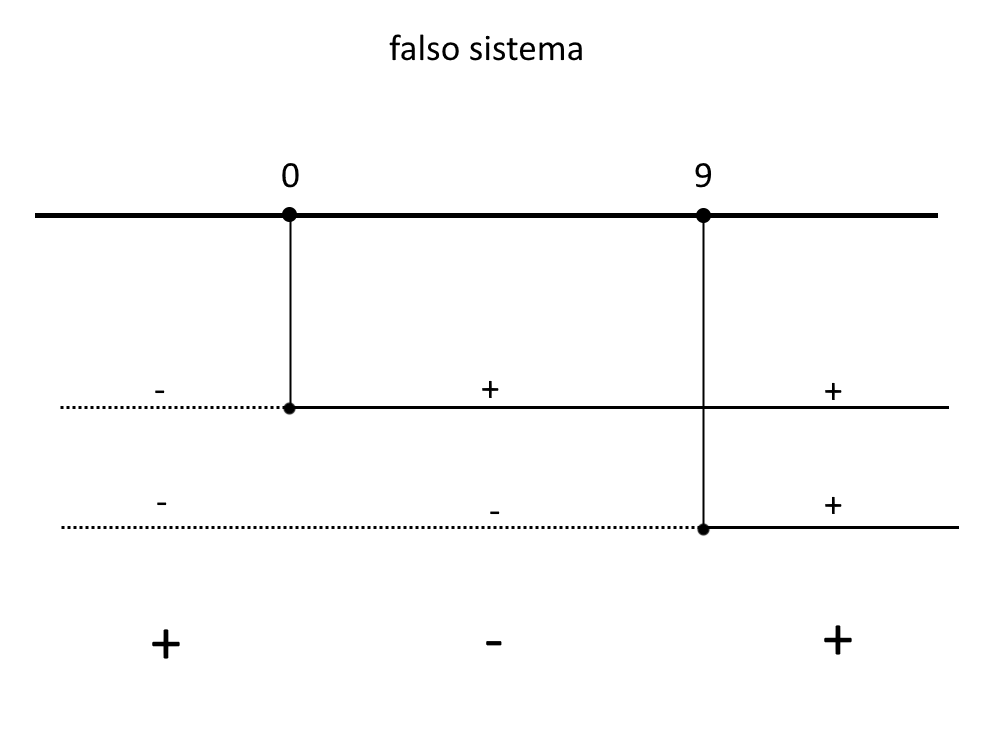
Ossia:
CE: x \le 0 \lor x \ge 9
Adesso passiamo all’esercizio: siamo nelle condizioni giuste e quindi applichiamo subito la formula. Risolviamo il seguente sistema.
\begin{cases} 5-x \ge 0 \\ x^2 -9x =(5-x)^2 \end{cases}
\begin{cases} -x \ge -5 \\ x^2 -9x = 25 +x^2 -10x \end{cases}
Al primo cambiamo di segno, al secondo portiamo le x a primo membro:
\begin{cases} x \le 5 \\ x = 25 \end{cases}
Come possiamo vedere tale sistema non è soddisfatto per nessuna x. Cioè x=25 non rientra nell’intervallo del primo termine (x minore o uguale di 5). Quindi non c’è soluzione o è impossibile!
Esercizio 8. \sqrt{ x^2 -x +3 } -x = 1
CE: x^2 -x +3 \ge 0
Essa è una disequazione di secondo grado, quindi per la risoluzione calcoliamo il discriminante:
\Delta = b^2 -4ac = 1-12 =-11
Il Delta<0, ed in una disequazione con il \ge significa che c’è sempre soluzione (cliccateci sopra per le formule), quindi:
CE: \forall x
In pratica qualsiasi soluzione andrà bene.
Portiamo il -x a secondo membro per ottenere la forma giusta per la formula, ossia con la radice da sola a sinistra.
\sqrt{ x^2 -x +3 } = 1 +x
Risolviamo il solito sistema.
\begin{cases} 1+x \ge 0 \\ x^2 -x+3 = (1+x)^2 \end{cases}
\begin{cases} x \ge -1 \\ x^2 -x+3 = 1+x^2 +2x \end{cases}
Al secondo termine portiamo le x a primo membro.
\begin{cases} x \ge -1 \\ -3x = 1-3 \end{cases}
\begin{cases} x \ge -1 \\ x = \frac{2}{3} \end{cases}
La soluzione in comune è x = \frac{2}{3} .
Le CE ci dicevano che qualsiasi soluzione sarebbe andata bene, e quindi questa la teniamo!
Continuiamo con altre equazioni irrazionali esercizi svolti!
Esercizio 9. Calcolare le condizioni di esistenza della seguente equazione:
\frac{1}{2} \sqrt{ \frac{x+1}{x} } = x
Condizioni di esistenza: qui dobbiamo farla sia della radice che anche della frazione. Per la frazione significa porre il denominatore diverso da zero! Mettiamo a sistema le diverse CE per ottenere una unica CE:
CE: \begin{cases} \frac{x+1}{x} \ge 0 \\ x \ne 0 \end{cases}
La prima è una disequazione fratta, che la risolviamo da parte un attimo con un falso sistema.
\big\| x +1 \ge 0 \\ \big\| x > 0
(Ricordatevi che alla disequazione del denominatore non si mette mai l’uguale anche, perché non può essere uguale a zero per le CE)
\big\| x \ge -1 \\ \big\| x > 0
Nel quadro dei segni, prendiamo gli intervalli positivi:
x \le -1 \lor x>0
Sostituiamo questo risultato nel sistema iniziale!
CE: \begin{cases} x \le -1 \lor x>0 \\ x \ne 0 \end{cases}
E quindi riotteniamo sempre:
CE: x \le -1 \lor x>0
Esercizio 10. \sqrt[3]{ x^3 +x +2 } =x
Qui abbiamo una radice con indice dispari, non dimenticatevi mai che questa radici non hanno bisogno di CE, e seguono un’altra formula!
Quindi passiamo direttamente a seguire tale formula, che è equivalente ad elevare tutto alla terza.
\implies x^3 +x +2 =x^3
x +2 =0 \implies x=-2
Continuiamo con altre equazioni irrazionali esercizi svolti!
Equazioni irrazionali esercizi con due radicali
Esercizio 11. \sqrt{ x+4 } = \sqrt{ x^2 -16 }
Questo è il caso di due radicali all’interno della stessa equazione. Il primo punto è sempre lo stesso, ossia di scrivere le condizioni di esistenza, questa volta non più di un solo radicale ma di due. Quindi dobbiamo porre due radicandi maggiore o uguale a zero. Risolviamo il sistema in cui mettiamo ogni singola CE:
CE: \begin{cases} x+4 \ge 0 \\ x^2 -16 \ge 0 \end{cases}
CE: \begin{cases} x \ge -4 \\ x^2 \ge 16 \end{cases}
Il secondo termine ha come soluzioni le due radici con segno opposto, e poi si prendono di queste i valori esterni essendoci un maggiore o uguale.
x^2 = 16 \implies x = \pm 4 \implies x \le -4 \lor x \ge 4
CE: \begin{cases} x \ge -4 \\ x \le -4 \lor x \ge 4 \end{cases}
E quindi otteniamo come unica comune soluzione:
CE: x \le -4 \lor x \ge 4
Passiamo allo svolgimento. Ci sono diversi modi di agire: ora vediamo il primo caso. Quando abbiamo due sole radici con segno positivo davanti ad entrambe (cioè non ad es. - \sqrt{}) allora quello che facciamo è elevare solamente tutto al quadrato.
(\sqrt{ x+4 })^2 = (\sqrt{ x^2 -16 } )^2
x+4 = x^2 -16
Abbiamo una equazione di secondo grado, quindi riordiniamola portando tutto a primo membro:
-x^2 +16 +x+4 = 0
-x^2 +x+ 20 = 0
Il coefficiente della x^2 è negativo, e come detto nella pagina dedicata alle equazioni di secondo grado, conviene cambiare tutto di segno.
x^2 -x - 20 = 0
Solo adesso possiamo calcolare il delta:
\Delta = b^2 - 4ac = 1 + 80 = 81
Delta>0 ed esistono quindi due soluzioni. Calcoliamole con la formula:
x_{1,2} = \frac{-b \pm \sqrt{\Delta} }{2a} = \frac{ 1 \pm 9 }{2}
E quindi:
x_1 = \frac{ 1 + 9 }{2} = 5
x_2 = \frac{ 1 - 9 }{2} = -4
Abbiamo trovate finalmente le due soluzioni: ora dobbiamo controllare se vanno bene, quindi mettiamole a sistema con le CE.
\begin{cases} x=-4 \lor x=5 \\ x \le -4 \lor x \ge 4 \end{cases}
Vanno bene entrambe perchè rientrano negli intervalli delle CE! L’esercizio è concluso con le soluzioni x=-4, x=5!
Esercizio 12. \sqrt{ (x+3)(x-3) } - \sqrt{ 5x-3 } =0
Prima di ragionare sul da farsi, facciamo ciò che è sicuro fare: ossia le condizioni di esistenza, CE di tutte e due le radici. Quando ci sono più CE mettiamole a sistema che è più comodo il tutto!
CE: \begin{cases} (x+3)(x-3) \ge 0 \\ 5x-3 \ge 0 \end{cases}
Il secondo termine è immediato, scriviamo direttamente il risultato.
CE: \begin{cases} (x+3)(x-3) \ge 0 \\ x \ge \frac{3}{5} \end{cases}
Il primo termine invece è una disequazione con un prodotto, che si risolve con un falso sistema scritto un attimo da parte.
\big\| x+3 \ge 0 \\ \big\| x-3 \ge 0
Qui, essendo un prodotto, tutte e due i termini del falso sistema contengono l’uguale anche. Piccola parentesi: qualche caso fa c’era una frazione e quindi la disequazione relativa al denominatore non poteva contenere l’uguale, qui c’è un prodotto.
\big\| x \ge -3 \\ \big\| x \ge 3
Prendiamo gli intervalli positivi nello schema dei segni, ossia:
x \le -3 \lor x \ge 3
Sostituiamo tale risultato nel sistema iniziale delle CE.
CE: \begin{cases} x \le -3 \lor x \ge 3 \\ x \ge \frac{3}{5} \end{cases}
Ricaviamo una unica CE comune che è:
CE: x \ge 3
Passiamo all’esercizio: questo si può ricondurre al caso precedente, ossia una radice a sinistra ed una a destra senza nient’altro. Portiamo quindi la seconda radice a secondo membro:
\sqrt{ (x+3)(x-3) } = \sqrt{ 5x-3 }
Come detto già prima, in tali casi, l’unica cosa da fare è elevare tutto al quadrato in modo da levare le radici e poi risolvere quello che esce fuori!
(\sqrt{ (x+3)(x-3) })^2 = (\sqrt{ 5x-3 } )^2
(x+3)(x-3) = 5x-3
Il primo termine è immediato se usiamo la formula della differenza di quadrati:
a^2 - b^2 = (a-b)(a+b)
Quindi nel nostro caso:
x^2 - 9 = 5x-3
Portiamo tutto a primo membro perché abbiamo di fronte ancora una volta una equazione di secondo grado.
x^2 - 9 - 5x+3 = 0
x^2 - 5x -6 = 0
Calcoliamo il discriminante:
\Delta = b^2 - 4ac = 25 + 24 = 49
Delta>0 ed esistono quindi due soluzioni. Troviamole:
x_{1,2} = \frac{-b \pm \sqrt{\Delta} }{2a} = \frac{ 5 \pm 7 }{2}
E così le singole soluzioni dell’esercizio sono:
x_1 = \frac{ 5 + 7 }{2}= 6
x_2 = \frac{ 5 - 7 }{2} = -1
Controlliamo se queste due soluzioni vanno bene, mettiamole a sistema con le CE per vedere se qualcuna bisogna scartarla.
\begin{cases} x = 6 \lor x= -1 \\ x \ge 3 \end{cases}
Di conseguenza prendiamo solamente la soluzione x=6 essendo che le CE ci dicono che la soluzione deve essere maggiore o uguale di 3.
Esercizio 13. \sqrt{ 27+x } -\sqrt{ x } = 3
CE: \begin{cases} 27+x \ge 0 \\ x \ge 0 \end{cases}
CE: \begin{cases} x \ge -27 \\ x \ge 0 \end{cases}
E quindi l’unica CE comune è:
CE: x \ge 0
Qui abbiamo oltre le due radici, anche un altro numero: è un caso un po’ diverso, ma i passaggi non saranno poi così diversi, quindi tranquilli!
Come prima cosa isoliamo una radice a primo membro e portiamo tutto il resto dall’altra parte:
\sqrt{ 27+x } = \sqrt{ x } + 3
L’importante è avere la prima radice con un segno positivo davanti (cioè non vogliamo - \sqrt{} ).
Ora prima di andare avanti bisogna fare una cosa: VERIFICARE che il secondo membro sia positivo. Di solito ci si arriva quando si può senza calcoli, ma semplicemente spiegando il perché è positivo. Qui ad esempio abbiamo un 3 e poi una radice che è sicuramente positiva per definizione, quindi 3+ qualcosa di positivo= positivo!
E solo a questo punto si può andare avanti col punto successivo: elevare tutto al quadrato!
(\sqrt{ 27+x })^2 = (\sqrt{ x } + 3)^2
27+x = x+9 + 6\sqrt{x}
Semplifichiamo la x. Qui poi ci ricolleghiamo ad un caso che abbiamo già visto, ossia quello in cui avevamo:
\sqrt{ A(x) } = k
Di fatti isoliamo la radice a primo membro:
-6 \sqrt{x} = -18
Cambiamo tutto di segno e poi dividiamo per 6, per avere solamente la radice a sinistra.
\sqrt{x} = 3
Ora siamo nelle condizioni di applicare la formula classica che abbiamo usato tante volte. Quindi risolviamo il sistema:
\begin{cases} 3 \ge 0 \\ x = 3^2 \end{cases}
\begin{cases} \forall x \\ x = 9 \end{cases}
Di conseguenza la soluzione è x=9.
Mettiamola a sistema con le CE per vedere se va bene:
\begin{cases} x=9 \\ x \ge 0 \end{cases}
E quindi come soluzione x=9 va bene perchè è maggiore o uguale di 0!
Esercizio 15. \sqrt{ x-3 } - \sqrt{ x+2 } = 5
CE: \begin{cases} x-3 \ge 0 \\ x+2 \ge 0 \end{cases}
CE: \begin{cases} x \ge 3 \\ x \ge -2 \end{cases}
Ossia CE: x \ge 3
Ora passiamo alla risoluzione dell’esercizio: questo è esattamente il caso dell’esercizio precedente, quindi seguiamo gli stessi passaggi. Isoliamo la prima radice:
\sqrt{ x-3 } = \sqrt{ x+2 } + 5
Adesso sulla sinistra abbiamo una radice sola che è positiva o al massimo uguale a zero: dobbiamo verificare prima di procedere se anche il secondo membro è positivo o uguale a zero. E di fatti come prima abbiamo un 5 + una radice = sicuramente positivo!
Possiamo procedere: eleviamo tutto al quadrato! (Se il secondo membro risultasse negativo non si poteva procedere e si scriveva impossibile)
(\sqrt{ x-3 })^2 = (\sqrt{ x+2 } + 5 )^2
x-3 = x+2 + 25 + 10 \sqrt{ x+2 }
Semplifichiamo la x:
-3 = +2 + 25 + 10 \sqrt{ x+2 }
Portiamo la radice a primo membro e tutto il resto al secondo: ciò che vogliamo fare è ricollegarci al caso:
\sqrt{A(x)}= k
- 10 \sqrt{ x+2 } = 30
Adesso vogliamo la radice isolata, cambiamo tutto di segno e poi dividiamo per 10:
\sqrt{ x+2 } = -3
Abbiamo una radice che non può mai essere negativa né tanto meno uguale a -3, quindi la soluzione è impossibile.
Se non siete convinti, procediamo passo dopo passo, applicando la formula e risolvendo il sistema:
\begin{cases} -3 \ge 0 \\ x+2 = (-3)^2 \end{cases}
Il primo termine chiaramente non può mai essere maggiore o uguale a zero, perché è -3 sempre e quindi non esiste nessuna x tale per cui quella disequazione venga soddisfatta.
\begin{cases} \nexists x \\ x+2 = (-3)^2 \end{cases}
Non serve continuare perché se non esiste nessuna x, visto che in un sistema si prendono le soluzioni comuni, allora non esisterà nessuna soluzione comune. Quindi è impossibile!
In questa pagina abbiamo visto quali sono le formule da utilizzare per saper risolvere qualsiasi equazione irrazionale.
Per approfondire:
https://it.wikipedia.org/wiki/Equazione_irrazionale
Equazioni irrazionali esercizi.
valore
assoluto
irrazionali
esercizi