Equazioni pure: ESERCIZI SVOLTI e FORMULE
Le equazioni pure sono un argomento importante, poiché ritorna molte volte durante tutto il Liceo. E’ importante dunque capire bene come si fanno. Non dovete preoccuparvi poiché non è nulla di impossibile, leggete con calma questa pagina e prenderete un bel voto nel compito in classe.
Indice
- Cosa sono le equazioni pure: definizione
- Formule per risolvere le equazioni pure
- ESERCIZI SVOLTI
- Equazioni pure impossibili
Fatta quindi questa piccola premessa, iniziamo col vedere cosa sono e come distinguere una equazione pura.
Cosa sono le equazioni pure: definizione
Prima di partire a bomba col mostrarvi degli esercizi e delle formule, bisogna un attimino comprendere e riuscire a distinguere una equazione pura.
Partiamo dalla forma usuale della equazione di secondo grado:
ax^2 +bx +c = 0
Partiamo da questo, poiché le equazioni pure sono un caso specifico delle equazioni di secondo grado. L’unica differenza è che ora il coefficiente b=0!
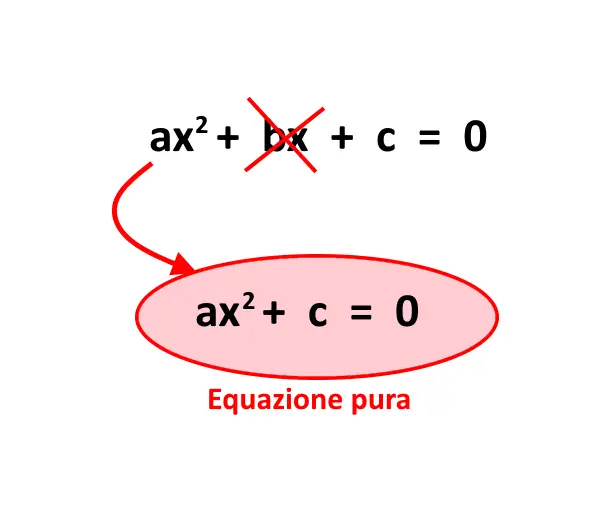
E allora non ho capito: le equazioni pure sono di secondo grado o no? Allora, proprio come detto nella pagina delle equazioni spurie, se il grado più alto dell’equazione è il termine x^2, allora essa si dirà di secondo grado. Poi siamo noi che andiamo a distinguere il sottocaso “equazione pura”!
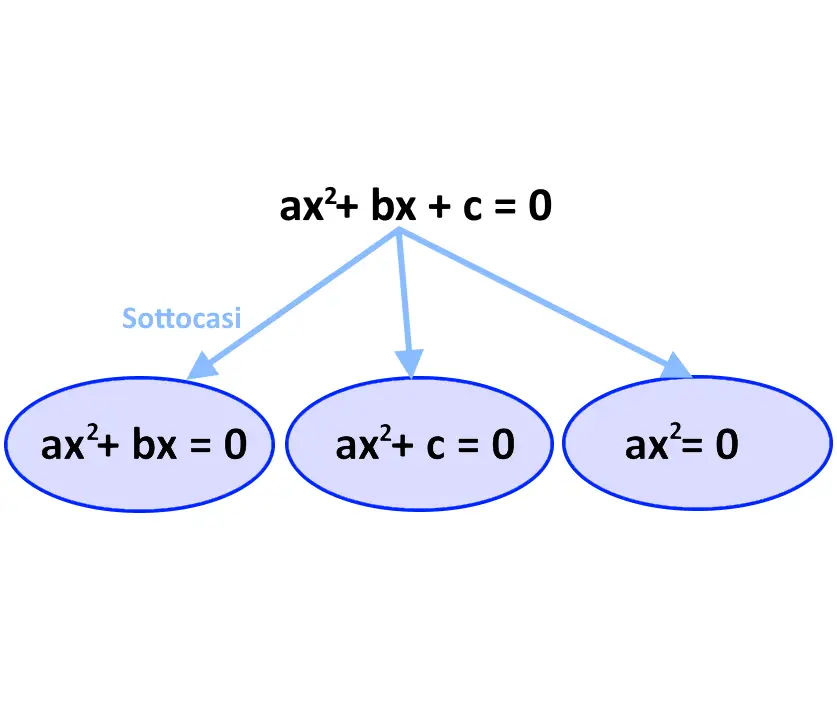
Ora che abbiamo capito come riconoscere una equazione pura, eccovi anche alcuni esempi per capire meglio di cosa stiamo parlando!

Ora siamo assolutamente pronti per andare a vedere come si risolvono! Nel prossimo paragrafo vedremo delle formule da usare, e dei passaggi da seguire per evitare di incorrere nell’errore.
Formule per risolvere le equazioni pure
Ricapitoliamo. Questa seguente è una equazione pura:
ax^2 +b = 0
Ed adesso come la risolviamo? Prima di arrivare alla formula da usare, vi facciamo vedere anche i passaggi che dovrete fare negli esercizi! Seguite con calma questo paragrafo e capirete tutto, senza confondervi o avere problemi con le formule.
L’obiettivo delle equazioni è sempre lo stesso: trovare la x. Quindi iniziamo ad isolare a sinistra la x:
ax^2 = -b
Vogliamo la x vero? E allora del coefficiente “a” non ci interessa. Dividiamo tutto per a:
\frac{ax^2}{a} = -\frac{b}{a}
A sinistra il coefficiente a si semplifica:
x^2= -\frac{b}{a}
Perfetto, e ora come facciamo? Adesso per la risoluzione ci servirà una delle seguenti due formulette.
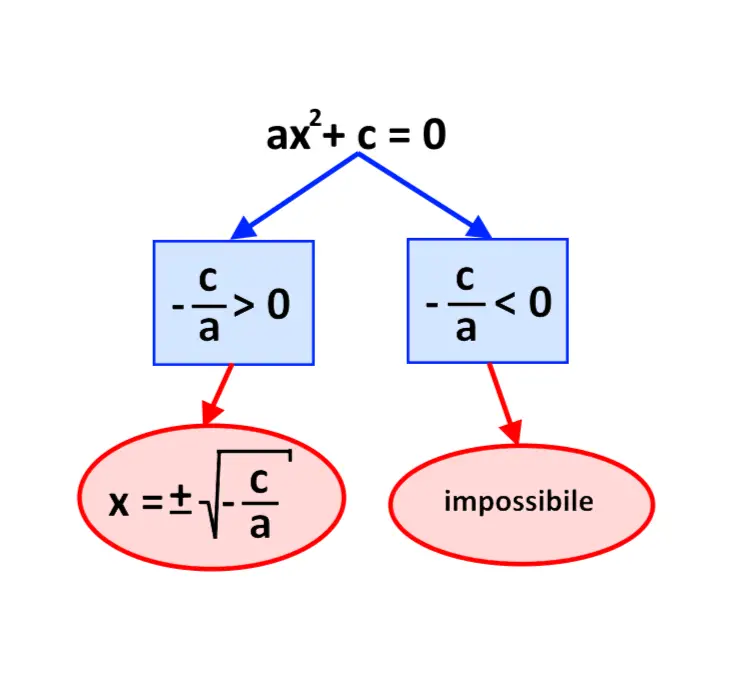
Ora prima di andare avanti nella pagina, vi PREGO di leggere queste righe. Iniziamo a commentare queste formule per capirle meglio. Non impariamole a memoria per favore.
Partiamo dal secondo caso: quello in cui se - \frac{b}{a} < 0 allora l’equazione è impossibile.
Questo è quello che succede quando ad esempio abbiamo:
x^2 = - 9
Tale caso vuol dire, in parole povere, che a destra abbiamo un numero negativo, tutto qui.
L’equazione è “impossibile”, cosa vuol dire e perché? Beh, ponetevi una domanda: esiste un numero che elevato al quadrato dia un numero negativo? No, poiché qualsiasi numero ci mettiamo al posto della x, ci verrà un numero positivo:
(3)^2 = 9>0
(-3)^2 = 9>0
Quindi non verrà mai -9 in nessun caso. L’equazione si dice “impossibile” o “senza soluzione”, ed ora avete capito il perché! Inoltre altra dimostrazione è che non si può usare la prima formula, perché altrimenti dovremmo fare:
x = \pm \sqrt{- 9}
E sappiamo che la radice di un numero negativo non esiste.
Passiamo al primo caso, quello della formuletta. Qui invece a destra abbiamo un numero positivo, ad esempio:
x^2 = 4
La prima formula ci dice che dobbiamo farne la radice, e prenderne sia la parte positiva che negativa. Perché?
Sul fatto del perché dobbiamo farne la radice è abbastanza ovvio, visto che abbiamo il termine quadratico x^2, quindi per ottenere solo “x” ne dobbiamo fare la radice. E allora ci aspettiamo che la soluzione sia solo:
\sqrt{x^2} = \sqrt{4}
x = 2
Però la formula ci dice di prendere anche la radice, con davanti il segno meno, ossia:
x_2 = -\sqrt{4} = -2
E come mai anche questa dobbiamo prendere? Vi basta eseguire una verifica della equazione per capirlo. La formula ci dice che le due soluzioni sono:
x_1 = 2, x_2 = -2
Proviamo a mettere questi due valori all’interno dell’equazione per vedere se ci troviamo, e se il libro ha ragione.
x^2 = 4
Mettiamoci il 2:
2^2 = 4
Giusto, sinistra è uguale a destra e quindi questa soluzione va bene. Mettiamo l’altra, quella col meno, quella che abbiamo più dubbi sul perché la si prende:
(-2)^2 = 4
Ecco la risposta: un termine negativo elevato al quadrato diventa positivo. Quindi dobbiamo prendere la radice, una col segno + e l’altra col segno -!
Ora che forse abbiamo capito a fondo le formule da usare, cerchiamo di consolidare, con degli esercizi.
ESERCIZI SVOLTI sulle equazioni pure
Gli esercizi saranno in difficoltà graduale, dai più semplici ai più difficili. Inoltre il paragrafo sulle equazioni pure impossibili sono alla fine, a parte.
Esercizio 1. x^2 - 6 = 0
Da ora in poi ci saranno esercizi, che vi mostreranno che non serve imparare a memoria quelle formule! Le svolgeremo con furbizia e col cervello.
L’obiettivo della equazione è ricavare la x, quindi isoliamo la x a sinistra:
x^2 = 6
Ricordiamo sempre di cambiare segno al termine, quando lo si porta dall’altra parte! A questo punto c’è il termine x al quadrato. A destra abbiamo un numero positivo, quindi possiamo farne la radice, o meglio le due radici con segno opposto:
x = \pm \sqrt{6}
Quindi le due soluzioni sono distintamente:
x_1 = + \sqrt{6}
x_2 = - \sqrt{6}
Esercizio 2. \frac{x^2}{\sqrt{5} } = 0
Dobbiamo avere la x a sinistra da sola. Come facciamo? Moltiplichiamo tutto per la radice di 5:
\frac{x^2}{\sqrt{5} } \sqrt{5} = 0 \cdotp \sqrt{5}
La frazione si semplifica, mentre a destra chiaramente fa zero.
x^2 = 0
A destra abbiamo un numero positivo, quindi dobbiamo applicare la prima formula, ossia in pratica fare la radice e prenderne i due segni:
x = \pm \sqrt{0}
La radice di zero fa zero. Quindi:
x = \pm 0
“Più zero” e “meno zero” sono la stessa cosa. Quindi abbiamo due soluzioni, uguali!
x_{1,2} = 0
Esercizio 3. 4x^2 - 16 = 0
Eccoci con un nuovo esercizio, la cui difficoltà aumenta gradualmente. Ora abbiamo anche un coefficiente attaccato al termine quadratico. Partiamo sempre con il tenere da sola la x a sinistra:
4x^2 = 16
Dopo di che non ci accontentiamo, vogliamo la x e basta o no? E allora dividiamo per 4:
x^2 = \frac{16}{4}
x^2 = 4
Il numero a destra è positivo, quindi c’è soluzione. Come la troviamo? Facendo la radice, e prendendo i due segni:
x= \pm \sqrt{ 4}
Le due soluzioni sono allora:
x_1 =2, x_2 = -2
Una prova che state facendo bene è che vi verranno sempre due segni opposti, ma con stesso numero.
Esercizio 4. \frac{2}{13} x^2 = 13
Abbiamo ora come coefficiente “a” una frazione. Con le frazioni spesso si sbaglia facilmente, anche con errori stupidi. Dunque facciamo un passaggio alla volta. L’obiettivo è levare quella frazione. Iniziamo a moltiplicare dunque tutto per 13:
13 \cdotp \frac{2}{13} x^2 = 13 \cdotp 13
A sinistra il denominatore va via, mentre a destra risulta comodo scriverlo come 13^2 (perché dopo dovremo fare la radice quadrata).
2 x^2 = 13^2
Ed adesso invece dividiamo tutto per 2, e ci siamo levati di mezzo il coefficiente attaccato al termine della x!
x^2 = \frac{ 13^2 }{2}
Il numero è positivo, dunque facciamo la radice e poi prendiamo entrambi i segni:
x = \pm \sqrt{ \frac{ 13^2 }{2} }
Sopra il quadrato se ne va con la radice quadrata, dunque la radice rimane solo giù.
x = \pm \frac{ 13 }{ \sqrt{2} }
Il libro potrebbe portare un risultato diverso, dovuto al passaggio solito della “razionalizzazione”. Questo passaggio consiste nel portare la radice su’. Come si fa? Si moltiplica e divide per la radice:
x = \pm \frac{ 13 }{ \sqrt{2} } \frac{ \sqrt{2}}{ \sqrt{2}}
Dunque:
x = \pm \frac{ 13\sqrt{2} }{ 2 }
Esercizio 5. - \sqrt{3}t^2 = -3
Osserviamo l’equazione che l’esercizio ci dà: notiamo che in entrambe le parti vi sono dei segni negativi, quindi la prima comodità che possiamo avere è quella di cambiare tutto di segno.
\sqrt{3}t^2 = 3
Cerchiamo di tenere solo la parte con la t quadratica, quindi dividiamo per la radice:
t^2 = \frac{3}{ \sqrt{3} }
A destra si ha un numero positivo, perché:
- il 3 al numeratore è positivo;
- la radice di 3 (basta farla sulla calcolatrice) fa 1,73 che è positivo.
Abbiamo la radice al denominatore, razionalizziamo.
t^2 = \frac{3}{ \sqrt{3} } \frac{ \sqrt{3} }{ \sqrt{3} }
t^2 = \frac{ 3\sqrt{3} }{ 3 }
Semplificando:
t^2 = \sqrt{3}
Quindi la soluzione finale sarà:
t = \pm \sqrt{\sqrt{3}}
Abbiamo la radice di una radice, ossia:
\sqrt{\sqrt{3}} = \sqrt[4]{3}
Quindi:
t = \pm \sqrt[4]{3}
Esercizio 6. 8( 4x^2 - 2 ) = 4^3
Maneggiamo in questo esercizio proposto dal libro dei numeri con potenze! Il consiglio che vi do è quello di lasciare tali numeri così come sono fino alla fine. E magari solo proprio alla fine levare la potenza e scriverli in esteso.
32x^2 - 16 = 4^3
32x^2 = 4^3 + 16
A questo punto dobbiamo per forza scriverlo estesamente (se non sapete come farlo basta che fate con la calcolatrice 4x4x4):
32x^2 = 64 + 16
32x^2 = 80
Dividiamo per 32:
x^2 = \frac{80}{32}
Con questi numeroni giganti semplifichiamo poco alla volta, facendo diviso 2 per il momento:
x^2 = \frac{40}{16}
E continuando a piccoli passi arriviamo a:
x^2 = \frac{5}{2}
L’esercizio è finito!
x = \pm \sqrt{ \frac{5}{2} }
Esercizio 7. ( \frac{x+1}{2} )^2 = \frac{1}{3} \cdotp \frac{3x}{2} + \frac{5}{4}
Questo già sembra un esercizio molto più complicato dei precedenti: contiene frazioni, quadrati e moltiplicazioni. Da cosa partiamo?
Partiamo da ciò che volete. Volendo rispettare l’ordine sinistra-destra, partiamo dal fare il quadrato della frazione. Come si fa? Il quadrato deve essere applicato al numeratore ed al denominatore, come nell’esempio.
( \frac{a}{b})^2 = \frac{a^2}{b^2}
Quindi otteniamo:
\frac{ (x+1)^2 }{4} = \frac{1}{3} \cdotp \frac{3x}{2} + \frac{5}{4}
E allora facciamo a sto punto anche il quadrato del binomio al numeratore!
\frac{ x^2 + 1 +2x }{4} = \frac{1}{3} \cdotp \frac{3x}{2} + \frac{5}{4}
Ok passiamo oltre. Facciamo la moltiplicazione fra quelle due frazioni:
\frac{ x^2 + 1 +2x }{4} = \frac{3x}{6} + \frac{5}{4}
Notiamo che si può semplificare la frazione! Facendo diviso 3:
\frac{ x^2 + 1 +2x }{4} = \frac{x}{2} + \frac{5}{4}
Come si levano le frazioni ora? Moltiplicando entrambi i lati per il denominatore più alto (4 in questo caso).
4 \cdotp \frac{ x^2 + 1 +2x }{4} = 4 \cdotp \frac{x}{2} + 4 \cdotp \frac{5}{4}
E semplificando viene fuori:
x^2 + 1 +2x = 2x + 5
x^2 + 1 +2x - 2x - 5 = 0
x^2 - 4 = 0
Ora concludiamo l’esercizio.
x^2 = 4 \implies x = \pm 2
Esercizio 8. 4(x+1)(x-2) = - ( 1+2x )^2
Qui abbiamo due passaggi in cui possiamo rincorrere nell’errore: uno è la moltiplicazione (per non sbagliare usate le dita per puntare i termini da moltiplicare) e poi il quadrato. Facciamoli. Il 4 davanti alle parentesi moltiplica tutto quindi lasciamolo!
4( x^2 -2x +x -2 ) = - ( 1+4x^2 + 4x )
Il segno meno anche non lo abbiamo levato, perché ci dice che dobbiamo cambiare i segni di tutti i termini a destra!
4x^2 -8x +4x -8 = - 1-4x^2 - 4x
Senza saper leggere né scrivere buttiamo tutto a sinistra e via!
4x^2 -8x +4x -8 + 1+4x^2 + 4x = 0
Sommiamo i termini simili.
8x^2 -7 = 0
8x^2 = 7
Poi:
x^2 = \frac{7}{8}
E giungiamo alla soluzione (sul libro questo esercizio di solito ha soluzione errata):
x = \pm \sqrt{ \frac{7}{8} }
Volendo si può anche pensare di razionalizzare, se volete, noi però ci scocciamo 🙂
Esercizio 9. ( a+ \sqrt{2} )^2 + ( \sqrt{2}a -1 )^2 = 6
La difficoltà di questo esercizio consiste nel saper maneggiare le radici, con le sue potenze e prodotti. L’unico passaggio insidioso è il primo, quello del svolgere i quadrati dei due binomi.
( a^2 + \sqrt{2}^2 + 2\sqrt{2}a ) + ( \sqrt{2}^2a^2 +1 - 2 \sqrt{2}a ) = 6
Il quadrato di una radice fa “semplificare” la radice (passatemi il termine terra terra).
( a^2 + 2 + 2\sqrt{2}a ) + ( 2a^2 +1 - 2 \sqrt{2}a ) = 6
Possiamo levare le parentesi: ci sono dei segni + prima di esse, e dunque possiamo stare tranquilli.
a^2 + 2 + 2\sqrt{2}a + 2a^2 +1 - 2 \sqrt{2}a = 6
Sommiamo:
3a^2 + 2 +1 = 6
3a^2 = 3
Di conseguenza ricaviamo, dividendo tutto per 3:
a^2 = 1
A questo punto ne facciamo la radice, sapendo che la radice di 1 è di nuovo 1!
a = \pm 1
Vediamo adesso delle equazioni pure, cui non c’è soluzione. Le cosiddette equazioni pure impossibili.
Equazioni pure impossibili
Esercizio 1. x^2 + 36 = 0
Iniziamo a vedere le equazioni pure impossibili, qualche esercizio che ci darà quindi questo risultato. Come nel paragrafo precedente, non dobbiamo fare nulla di diverso all’inizio, sempre isolare la x.
x^2 = -36
A questo punto ci dobbiamo porre la seguente domanda: il numero a destra è positivo o negativo? E’ chiaramente negativo.
Poi ci poniamo un’altra domanda. Esiste un numero che elevato al quadrato (x^2) dia come risultato un numero negativo? No. Quindi l’equazione pura si dice impossibile.
Come abbiamo detto nel paragrafo iniziale, impossibile significa senza risultato, senza soluzione.
Esercizio 2. b(b-4) = -4(b+1)
Nel corso delle varie pagine da noi offerte gratis, ci è capitato tante volte di non avere la solita “x”, ma di vedere una lettera diversa. Come agiamo quindi?
Una incognita o variabile la possiamo chiamare come vogliamo. Solitamente si dà il nome di x, ma in questo caso non dobbiamo preoccuparci. L’obiettivo dell’esercizio è trovare la “b”! Iniziamo a svolgere le moltiplicazioni:
b^2 -4b = -4b -4
Portiamo il termine -4b a sinistra (vogliamo sempre tutta la parte di incognita a sinistra):
b^2 = -4
Siamo giunti alla forma classica dell’equazione pura. Il numero a destra è negativo, e dunque è impossibile.
Esercizio 3. \sqrt{5} (y+0,5) + (y-1)^2 = -y ( 2- \sqrt{5} )
Osservando l’equazione capiamo che abbiamo un bel po’ di cose da fare. Partiamo dalla più semplice: riscrivere il termine con la virgola (0,5) in frazione.
\sqrt{5} (y+ \frac{1}{2} ) + (y-1)^2 = -y ( 2- \sqrt{5} )
Poi ci possiamo concentrare sul quadrato del binomio, ricordando di usare la formula seguente.
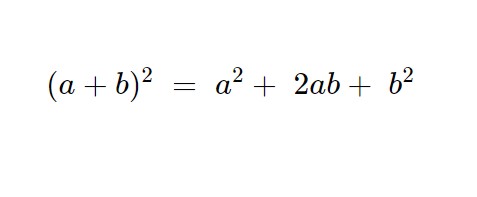
\sqrt{5} (y+ \frac{1}{2} ) + y^2 + 1 - 2y = -y ( 2- \sqrt{5} )
Ci rimane da levare quelle due parentesi tonde. Facciamo la moltiplicazione, ed il primo passo è stato fatto.
\sqrt{5}y+ \frac{ \sqrt{5} }{2} + y^2 + 1 - 2y = -2y + \sqrt{5}y
Nella seconda parentesi, ricordate che il segno meno davanti cambia il segno di tutti i termini contenuti all’interno.
Calcolare la y: portiamo tutte le y a sinistra ed il resto a destra.
\sqrt{5}y + y^2 - 2y +2y - \sqrt{5}y = -1 - \frac{ \sqrt{5} }{2}
y^2 = -1 - \frac{ \sqrt{5} }{2}
A secondo membro non abbiamo bisogno di fare nessun minimo comune multiplo, se ve lo state chiedendo. Perché? Perché possiamo già dire che a destra ci sarà sicuramente un numero negativo.
Come mai? Ragionate: se fate -1 – qualcos’altro sicuro vi darà un numero negativo!
L’equazione pura è impossibile.
Esercizio 4. (10^3 x + 0,1 )^2 = 200x
Qui abbiamo due scelte: la prima è continuare a portare il numero con la virgola (solo se avete la calcolatrice o se sapete fare a mano la moltiplicazione con esso), la seconda scelta è (senza calcolatrice) trasformare in frazione.
Di solito nei compiti in classe si usa la calcolatrice, quindi adotteremo il primo metodo. Svolgiamo il quadrato del binomio, facendo il quadrato di 0,1 con la calcolatrice. Anche 10^3 = 1000 lo potete fare con la calcolatrice. Basta che fate shift, poi cliccate “log” e poi scrivete 3.
1000^2x^2 + 0,01 + 2 \cdotp 0,1 \cdotp 1000 x = 200x
1000^2x^2 + 0,01 + 2 \cdotp 100 x = 200x
1000^2x^2 + 0,01 + 200 x = 200x
Portiamo le x a primo membro:
1000^2x^2 + 200 x - 200x = - 0,01
1000^2x^2 = - 0,01
Non serve nemmeno dividere tutto, a destra sta un numero negativo. Impossibile!
Esercizio 5. ( 2y + \sqrt{3} -1 )^2 + 4y = 2\sqrt{3} (2y-1)
Possiamo partire dalla cosa più facile a destra, levando la parentesi:
( 2y + \sqrt{3} -1 )^2 + 4y = 4\sqrt{3}y - 2\sqrt{3}
A sinistra abbiamo il cosiddetto “quadrato di un trinomio”. Questo è molto raro, anche nei compiti, quindi è inutile imparare la formula (lunga) a memoria. E allora come facciamo? Scriviamo per esteso la moltiplicazione, e poi moltiplichiamo tutti i termini singolarmente, non lasciandone neanche uno.
( 2y + \sqrt{3} -1 )( 2y + \sqrt{3} -1 ) + 4y = 4\sqrt{3}y - 2\sqrt{3}
Ora facciamo la moltiplicazione (primo per il primo, primo per il secondo, ecc.). Come prova che state facendo bene, essendo 3×3, vi dovranno venire 9 termini. Vediamo!
4y^2 + 2\sqrt{3}y - 2y + 2\sqrt{3}y + \sqrt{3}^2 - \sqrt{3} -2y - \sqrt{3} +1 + 4y = 4\sqrt{3}y - 2\sqrt{3}
Eh sì bello lunghetto. Tra l’altro è facile sbagliare quindi ricontrollate. Portiamo tutto a primo membro e sommiamo tutto quello che possiamo sommare!
4y^2 + 2\sqrt{3}y - 2y + 2\sqrt{3}y + \sqrt{3}^2 - \sqrt{3} -2y - \sqrt{3} +1 + 4y - 4\sqrt{3}y + 2\sqrt{3} = 0
Sommiamo:
4y^2 + \sqrt{3}^2 - \sqrt{3} - \sqrt{3} +1 + 2\sqrt{3} = 0
4y^2 + 3 - 2\sqrt{3} +1 + 2\sqrt{3} = 0
Sommiamo ancora:
4y^2 +4 = 0
Eccoci qui alla fine! Portiamo il 4 a destra e finalmente l’equazione è impossibile…in tutti i sensi!
4y^2 = -4
Questa lunga pagina finalmente è giunta alla fine. Gli argomenti toccati segnateveli, poiché vi ritorneranno utili nel corso degli anni del Liceo e dell’Università, questo è un argomento di base! Se notate errori contattateci per email a riferirci tutto!