ESERCIZI derivate: 25 esercizi SVOLTI
ESERCIZI derivate: 25 esercizi SVOLTI! In questa pagina vedremo come risolvere esercizi di derivate di tutti i tipi e di tutte le funzioni possibili: un paio di giorni su questa pagina e sarete pronti per la verifica in classe! Iniziamo subito a vedere come risolvere gli esercizi guidati sulle derivate: passo dopo passo spiegheremo ogni passaggio mostrando il procedimento e la soluzione. Ci sono due indici dove potete cliccare: uno è per esercizi liceali, l’altro universitari.
Indice Liceo
- Formule derivate
- Derivate di una somma di funzioni
- Derivate di una frazione
- Derivate di una radice
- Derivate esponenziale e logaritmo
- Derivata di seno e coseno
- Derivata di un prodotto di funzioni
- Derivata del quoziente di funzioni
- Derivata di funzioni composte
- Esercizi difficili sulle derivate
Iniziamo subito a vedere le proprietà e formule che useremo, prima di vedere come risolvere gli esercizi derivate.
Formule derivate


Possiamo iniziare con gli esercizi sulle derivate svolti, partiamo dal caso base: esercizi sulle derivate di una somma di funzioni.
Esercizi derivate: somma di funzioni
In questi esercizi sulle derivate di una somma di funzioni utilizzeremo la seguente formula:
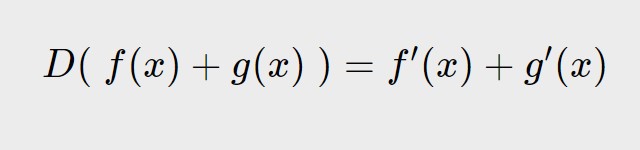
Partiamo subito: vedremo diverse funzioni una alla volta!
Esercizio 1. y=x^3 + x^2
Come potete vedere abbiamo una somma di due funzioni diverse: ossia abbiamo x^3 sommato a x^2. Come vedete dalla formula sopra, la derivata di tutto è semplicemente la derivata dei singoli termini.
In questo caso abbiamo due funzioni per la quale la derivata, come vedete in tabella, è:
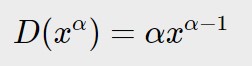
Di conseguenza la derivata del primo termine è:
D(x^3)= 3x^2
Mentre la derivata del secondo termine è:
D(x^2)=2x
La derivata di tutto è semplicemente la somma delle singole derivate, e quindi:
y' = 3x^2 + 2x
Esercizio 2. y=2x^2 - 3x +4
Anche qui come potete vedere abbiamo delle somme di singoli termini, quindi è lo stesso caso precedente: la derivata di tutto (y’) è semplicemente la somma delle singole derivate. Partiamo dal primo termine, abbiamo una costante (2) che moltiplica x^2, le costanti moltiplicative non danno mai problemi. Quello che si fa è calcolare la derivata della funzione, che in questo caso è x^2 e poi moltiplicarla alla fine per 2.
Quindi calcoliamo prima la derivata di x^2, usando la stessa formula di prima.
D(x^2)=2x
E poi solo dopo aver calcolato la derivata, la moltiplichiamo per la costante, che è 2. E quindi diventa:
2 \cdotp 2x = 4x
Ed il primo termine ce l’abbiamo! Adesso passiamo al secondo. Anche qui prendiamo sempre la funzione da derivare, e non le costanti. Dobbiamo derivare quindi solo la funzione x. Usiamo la formula:
D(x) = 1
Quindi la sua derivata è 1, adesso moltiplichiamo questa per la sua costante moltiplicativa.
-3 \cdotp 1 = -3
Passiamo adesso al terzo ed ultimo termine, questo è semplice perché la derivata di una qualsiasi costante è sempre zero.
D(k)=0
Adesso che abbiamo calcolato la derivata di ogni singolo termine, sommiamoli fra loro:
y'= 4x-3
Vediamo adesso come comportarsi quando dobbiamo c’è la derivata di una somma di funzioni fratte.
Esercizi derivate di una frazione
Esercizio 3. y= \frac{1}{x} + \frac{1}{x^2} + \frac{1}{x^3}
Adesso vediamo come comportarci quando abbiamo a che fare con delle funzioni fratte. Dobbiamo semplicemente fare un passaggio in più rispetto a prima: sfruttando una delle proprietà delle potenze possiamo scrivere una frazione come una potenza:
y= x^{-1} + x^{-2} + x^{-3}
E quindi non c’è nulla di nuovo, ci siamo ricondotti esattamente al caso precedente. Di fatti usiamo sempre la solita formula:
D(x^{\alpha}) = \alpha x^{\alpha -1}
L’unica accortezza è stare attenti ai segni meno. Proprio come prima allora, partiamo con la derivata del primo termine:
D(x^{-1}) = -1 \cdotp x^{-2} = - \frac{1}{x^2}
Alla fine ritorniamo alla forma delle frazioni per comodità. Passiamo al secondo termine:
D(x^{-2}) = -2 \cdotp x^{-3} = - \frac{2}{x^3}
E poi all’ultimo:
D(x^{-3}) = -3 \cdotp x^{-4} = - \frac{3}{x^4}
Sommiamo tutti i termini ed otteniamo la derivata y’ di tutto:
y' = - \frac{1}{x^2} - \frac{2}{x^3} - \frac{3}{x^4}
Volendo possiamo anche fare ora il mcm per una forma più compatta ma non è necessario.
Esercizio 4. y= \frac{1}{2}x^4 - \frac{2}{3}x^3 -5x^2 +2x -4 +\frac{1}{2x}
La storia è sempre la stessa in una somma: facciamo la derivata delle singole funzioni, e poi alla fine le sommiamo. Partiamo con la derivata del primo termine:
D(x^4)= 4x^3
E poi gli moltiplichiamo la sua costante:
\frac{1}{2} \cdotp 4x^3 = 2x^3
Secondo termine:
D(x^3)= 3x^2
Poi gli moltiplichiamo la sua costante con il segno meno anche!
- \frac{2}{3} \cdotp 3x^2 = -2x^2
Ed andiamo avanti con gli altri termini. Possiamo anche scrivere nel modo seguente per una maggior velocità:
D(-5x^2) = -5 \cdotp 2x = -10x
D(2x) = 2
D(-4) = 0
D(\frac{1}{2x})
Questo termine sopra per non confonderci mai, separiamo innanzitutto costante e funzione fratta:
D(\frac{1}{2} \frac{1}{x})
E poi scriviamo la frazione come potenza:
D( \frac{1}{2} x^{-1} ) = \frac{1}{2} \cdotp (-x^{-2})
=-\frac{1}{2} \frac{1}{x^2}=-\frac{1}{2x^2}
Sommiamo tutti i contributi ed abbiamo concluso il calcolo della derivata di questo esercizio!
y' = 2x^3-2x^2 -10x +2 -\frac{1}{2x^2}
Vediamo come comportarci se davanti a noi ci si presenta una radice!
Esercizi derivate di una radice
Esercizio 5. y= 2\sqrt{x} - \frac{1}{x}
Qui abbiamo una somma sempre, fra una radice ed una frazione. Anche la radice può essere riscritta come una potenza e quindi ricollegarci sempre alla solita formula. Grazie alla settima proprietà delle potenze, la nostra radice può essere scritta come:
2\sqrt{x} = 2 x^{ \frac{1}{2} }
Ed a questo punto ci siamo ricondotti ad una potenza. Per ricordarvi, basta mettere al denominatore l’indice della radice. Facciamone la derivata:
D( 2 x^{ \frac{1}{2} } ) = 2 \cdotp \frac{1}{2} x^{ \frac{1}{2} -1 }
Semplifichiamo il 2 e facciamo il minimo comune multiplo all’esponente:
= x^{ -\frac{1}{2} } = \frac{1}{ \sqrt{x} }
Facciamo la derivata dell’altro termine:
D(- \frac{1}{x} ) = -x^{-1} = - \cdotp -x^{-2} = \frac{1}{x^2}
Sommiamo ed otteniamo il risultato dell’esercizio:
y'= \frac{1}{ \sqrt{x} } + \frac{1}{x^2}
Esercizio 6. y= \sqrt[4]{x^3} + 3x -2
Adesso vediamo un caso importante da tenere a mente, ossia quando abbiamo una radice e dentro una x elevata a qualcosa.
Usando sempre la settima proprietà delle potenze, vedete bene che una radice può essere scritta come una potenza: di cui l’indice va al denominatore, mentre al numeratore ci mettiamo la potenza della x in pratica. Ossia:
\sqrt[4]{x^3} = x^{ \frac{3}{4} }
E da qui usiamo sempre la solita formula per calcolare la derivata:
D( x^{ \frac{3}{4} } ) = \frac{3}{4} x^{ \frac{3}{4}-1 } =
= \frac{3}{4} x^{ -\frac{1}{4} } = \frac{3}{4} \frac{1}{\sqrt[4]{x} }
Poi:
D(3x) = 3
D(-2) = 0
Sommiamo ed abbiamo finito il calcolo di questa derivata, con radici.
y' = \frac{3}{4} \frac{1}{\sqrt[4]{x} } +3
Vediamo adesso degli esempi di derivate con la presenza di esponenziali e logaritmi.
Esercizi derivate di un esponenziale e logaritmo
Esercizio 7. y= 2e^x - 3 \ln x
L’esponenziale semplice possiede la formula della derivata più semplice:
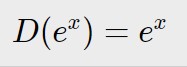
Bellissimo! Di fatti:
D(2e^x)=2e^x
Cioè ci ritorna a dare l’esponenziale! Mentre per il logaritmo naturale:
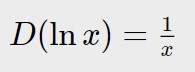
D(3\ln x ) =3 \frac{1}{x}
Sommiamo ed otteniamo:
y' = 2e^x + 3\frac{1}{x}
Esercizio 8. y=2^x + \log_3 x
Il primo termine è un esponenziale in base 2, quando la base è generale la formula che si usa è:
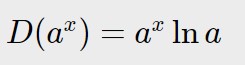
Quindi nel nostro caso:
D(2^x) = 2^x \ln 2
Passiamo al secondo termine, che è un logaritmo in base generale (3) e si usa la seguente formula.
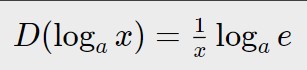
Nel nostro caso quindi:
D( \log_3 x) = \frac{1}{x} \log_3 e
Sommiamo ed abbiamo finito l’esercizio. C’è da dire una cosa però dopo.
y' = 2^x \ln 2 + \frac{1}{x} \log_3 e
Le due formule usate in questo esercizio in particolare c’è da dire però che sono meno frequenti negli esercizi. C’è da dire che nella verifica sicuramente un termine così la professoressa ve lo metterà…
Vediamo come fare le derivate adesso delle funzioni goniometriche: seno, coseno, tangente e cotangente.
Esercizi derivate seno e coseno
Esercizio 9. y=4x + 3\sin x -2\cos x -1
Abbiamo qui la somma di diverse funzioni, tra cui seno e coseno. Per esse usiamo le formule seguenti, molto utilizzate, quindi tenetele a mente!
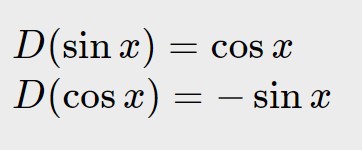
Usando queste iniziamo a fare le derivate:
D(4x)=4
D(3\sin x) = 3 \cos x
Adesso facciamo la derivata del coseno, che comporta sempre più errori: il segno cambia quindi bisogna stare attenti al segno finale, soprattutto se come in questo caso anche la costante moltiplicativa ha un meno!
D(-2\cos x) = -2 \cdotp (- \sin x ) = -2\sin x
D(-1)=0
Otteniamo quindi:
y'= 4 +3 \cos x -2\sin x
Come vedete le formule sono tante, quindi scrivetele mano mano tutte su un foglio e piano piano le memorizzerete. (Altrimenti scritte su un foglietto e via, però fate gli esercizi perché su alcune formule bisogna stare attenti)
Esercizio 10. y=\tg x - \cotg x
Arriviamo alle due ultime formule di questo capitolone sulla derivata di una somma di funzioni.
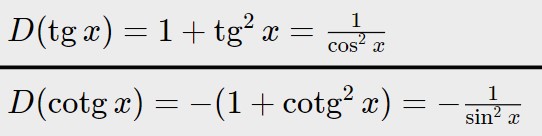
La prima uguaglianza solo a volte conviene, se per esempio gli altri termini escono fuori in tangente. Qui però essendo un caso semplice, usiamo la seconda uguaglianza nella formula.
D(\tg x) = \frac{1}{\cos^2 x}
D(-\cotg x) = - \cdotp -\frac{1}{\sin^2 x} =\frac{1}{\sin^2 x}
E di conseguenza:
y' = \frac{1}{\cos^2 x} + \frac{1}{\sin^2 x}
Facciamo il minimo comune multiplo per un risultato più compatto:
y' = \frac{\sin^2 x + \cos^2 x }{\cos^2 x \sin^2 x }
Ricordandoci la prima relazione fondamentale della goniometria:
\sin^2 x + \cos^2 x = 1
Possiamo quindi riscrivere il numeratore semplicemente come:
y' = \frac{ 1}{\cos^2 x \sin^2 x }
Vediamo cosa succede con esercizi derivata di un prodotto di funzioni, anziché somma!
Esercizi Derivata del PRODOTTO di funzioni
Negli esercizi precedenti abbiamo visto come ci si comporta e come si risolvono esercizi con derivate di una somma di funzioni, adesso vediamo come svolgere esercizi derivate di un prodotto di funzioni. Useremo le seguenti due formule (per la maggioranza la prima formula) per il prodotto di funzioni.
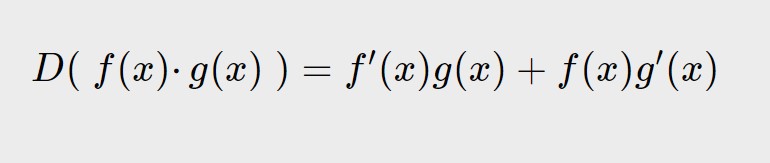
Esercizio 11. y= 3x \cdotp \ln x
Dando uno sguardo alla formula, in pratica noi abbiamo nel nostro caso che:
f(x) = 3x
g(x) = \ln x
Adesso calcoliamo anche le singole derivate, che ci servono nella formula:
f'(x) = 3
g'(x) = \frac{1}{x}
Ed ora applichiamo semplicemente la formula, stando attenti a mettere insieme i giusti termini!
y' = 3\ln x + 3x \frac{1}{x}
y' = 3\ln x +3
In pratica va prima la derivata di uno e poi dell’altro, invertendosi i ruoli!
Esercizio 12. y=5e^x \cdotp ( \sin x +x )
Qui abbiamo che si moltiplica un primo termine e poi una parentesi: sempre due termini sono! Quindi il procedimento è lo stesso. Identifichiamo con:
f(x) = 5e^x
g(x) = ( \sin x +x )
Calcoliamo le rispettive singole derivate:
f'(x) = 5e^x
g'(x) = (\cos x + 1)
Applichiamo la formula e sostituiamo i corrispettivi termini. Otteniamo:
y' = 5e^x ( \sin x +x ) + 5e^x(\cos x + 1)
Esercizio 13. y=3xe^x \tg x
Qui vediamo per completezza anche il caso in cui abbiamo un prodotto di tre funzioni (più raro in genere). Facciamo la stessa cosa, ossia scriviamo le tre funzioni:
f(x) = 3x
g(x) = e^x
h(x) = \tg x
E poi calcoliamo le derivate:
f'(x) = 3
g'(x) = e^x
h'(x) = \frac{1}{\cos^2 x}
Adesso passiamo alla formula: i termini sono tanti, quindi state super attenti e mettetene uno alla volta. Inoltre è fondamentale essere ordinati e ricontrollare! Non è nulla di difficile, semplicemente qui si possono fare errori stupidi. Otteniamo:
y' = 3e^x \tg x + 3x e^x \tg x + 3x e^x \frac{1}{\cos^2 x}
Vediamo adesso degli esercizi derivate sul quoziente di funzioni (ossia due funzioni che si dividono fra di loro).
Esercizi derivata del quoziente di funzioni
Per questo capitoletto, in cui affronteremo il calcolo della derivata di funzioni in una frazione (quindi sia una funzione al numeratore che al denominatore), useremo solo questa unica formula.
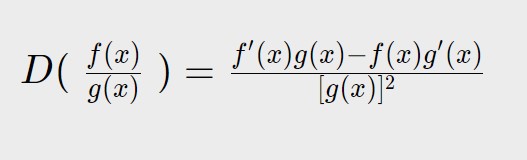
Esercizio 14. y=\frac{x^2}{2\ln x}
Il primo passo da fare è capire cosa abbiamo di fronte: come vedete abbiamo una funzione (x^2) al numeratore ed una funzione (2 ln x) al denominatore, quindi ricadiamo in questo nuovo caso nella quale dobbiamo utilizzare la formula sopra-scritta.
FATE ATTENZIONE! Bisogna avere una funzione al numeratore ed una al denominatore, quindi ad esempio la seguente:
y=\frac{2}{x}
NON rientra in questo caso, ma bensì in quello fatto all’inizio di questa pagina, riguardo la derivata di una frazione.
Ritorniamo all’esercizio. Scriviamo le due funzioni (cioè numeratore e denominatore) della formula nel nostro caso:
f(x)=x^2
g(x)=2 \ln x
Adesso calcoliamo le rispettive derivate:
f'(x)=2x
g'(x)=2 \frac{1}{x}
Poi ci manca il denominatore di ciò che verrà fuori, ossia il quadrato della funzione g(x):
g(x)^2 = 4 \ln^2 x
E sostituiamo il tutto nella formula, per risolvere l’esercizio:
y' = \frac{2x \cdotp 2 \ln x - x^2 \cdotp 2 \frac{1}{x} }{ 4 \ln^2 x }
ATTENZIONE che qui fra i due termini c’è un segno meno, mentre col prodotto non c’era!
y' = \frac{4x \ln x - 2x }{ 4 \ln^2 x }
Molto spesso gli esercizi con le derivate di un quoziente non si fermano all’applicazione della formula ma vanno avanti. Vanno avanti nel senso che bisogna cercare anche termini da semplificare ecc. per ottenere una forma più compatta. Qui mettiamo in evidenza il 2x:
y' = \frac{2x( 2\ln x -1) }{ 4 \ln^2 x }
y' = \frac{x( 2\ln x -1) }{ 2 \ln^2 x }
Questo è importante soprattutto con gli esercizi più complicati, nel quale semplificare ci permette di non avere calcoli troppo complicati.
Esercizio 15. y=\frac{x \sin x}{e^x}
Qui abbiamo a che fare con un esercizio esemplare, con un qualcosa di diverso rispetto all’esercizio precedente. Abbiamo sì una funzione al numeratore ed una al denominatore in frazione, tali che:
f(x)=x \sin x
g(x)= e^x
La cosa che cambia è che la f(x) è un prodotto di funzioni, per cui per la derivata usiamo la formula discussa già nel capitolo di prima.
f'(x)= (\sin x + x \cos x)
g'(x)=e^x
Inoltre:
g(x)^2 = (e^x)^2 = e^{2x}
Sostituiamo i rispettivi termini. Arriviamo alla derivata y’ che è:
y' = \frac{ (\sin x + x \cos x)e^x - x\sin x e^x }{e^{2x} }
L’esercizio non è concluso, mettiamo in evidenza il termine esponenziale:
y' = \frac{ e^x(\sin x + x \cos x - x\sin x ) }{e^{2x} }
E semplifichiamo:
y' = \frac{ \sin x + x \cos x - x\sin x }{e^x }
E mettiamo anche in evidenza per compattezza il seno:
y' = \frac{ \sin x(1-x) + x \cos x }{e^x }
Adesso vediamo quello che è il capitolo più importante di tutti, quello delle derivate di funzioni composte. In pratica tutta la verifica in classe volgerà attorno al prossimo capitolo.
Esercizi derivate di funzioni composte
Per questa parte di esercizi prenderemo in considerazione soprattutto la seconda parte della tabella, che è quella che dobbiamo assolutamente prendere familiarità.
Esercizio 16. y= (x^2 + 1)^8
Qui abbiamo una funzione del tipo seguente.
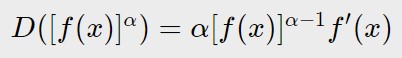
In cui c’è una funzione f(x) che è:
f(x)=(x^2 +1)
che è elevata tutta alla \alpha = 8
Per risolvere tale derivata, seguiamo passo passo la formula. Quindi non solo dobbiamo abbassare di grado l’esponente, ma dobbiamo poi moltiplicare il tutto per la derivata di quello che c’è dentro.
y' = 8 (x^2 +1 )^7 \cdotp 2x = 16x (x^2 +1 )^7
Esercizio 17. y= 2 \sin 5x
Qui abbiamo una funzione che è quella della seguente formula…formule che trovate tutte nella seconda parte della tabella.
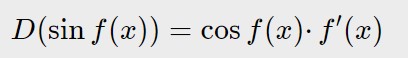
Dove nel nostro caso la funzione interna al seno f(x) è:
f(x)=5x
Quindi seguiamo passo passo la formula che ci dice in pratica che dobbiamo prima fare la derivata del seno senza considerare ciò che c’è dentro, e poi moltiplicare la derivata di ciò che c’è dentro. Questa è una politica a strati che ricorrerà molto spesso in questi esercizi: cioè partire dal fare la derivata della funzione più esterna fino a quella più interna. Scriviamo ciò che ci dice la formula:
y' = 2 \cos 5x \cdotp D(5x) = 2 \cos 5x \cdotp 5 = 10 \cos 5x
Esercizio 18. y= \sin \ln 2x
Adesso vediamo esattamente cosa significa fare le derivate a strati, quando ci sono più funzioni una dentro l’altra.
Qui quale formula prendiamo prima? Quella del seno? Quella del logaritmo? Quella della derivata di x?
La risposta è che si parte dal fare la derivata PIU’ ESTERNA! Partiamo da sinistra…ed incontriamo il seno! Quindi iniziamo ad utilizzare la formula del seno, usata nell’esercizio precedente:
y' = \cos (\ln 2x) \cdotp D(\ln 2x)
Adesso abbiamo diminuito le funzioni da derivare come vedete, dobbiamo fare la derivata solo di un logaritmo e di un 2x. Quale formula utilizziamo? Chiaramente quella del logaritmo adesso, perché partendo da sinistra è la prima funzione che incontriamo ALL’INTERNO SEMPRE DEL D( )!!! Non quella che incontriamo in generale, ma la prima che incontriamo all’interno del D()!!!
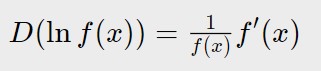
Quindi:
y' = \cos (\ln 2x) \cdotp \frac{1}{2x} \cdotp D(2x)
Adesso ci rimane solamente una funzione che sappiamo derivare facilmente! La derivata di 2x è 2! Otteniamo alla fine:
y' = \cos \ln 2x \cdotp \frac{1}{2x} \cdotp 2 = \frac{\cos \ln 2x }{x}
Questo significa fare le derivate a strati, partire dalla funzione più esterna o quella che sta più a sinistra e via via vedere cosa esce fuori da derivare ancora!
Esercizio 19. y=\ln \sin 3x
Anche qui stessa cosa, adottiamo il metodo del fare le derivate a strati, visto che abbiamo a che fare con una funzione composta dal logaritmo, dal seno, e poi dal 3x.
Partiamo da sinistra, incontriamo prima il logaritmo! Quindi usiamo prima di tutto la formula del logaritmo per fare la derivata di y!
y'=\frac{1}{\sin 3x} \cdotp D(\sin 3x)
Adesso all’interno della D(), ossia di ciò che dobbiamo derivare, dobbiamo seguire la formula della derivata del seno (sempre nella seconda parte della tabella mi raccomando! Queste sono funzioni composte quindi le formule da usare sono le ultime che trovate nella tabella):
y'=\frac{1}{\sin 3x} \cos 3x \cdotp D(3x)
E facciamo l’ultima semplice derivata e l’esercizio è concluso:
y'=\frac{1}{\sin 3x} \cos 3x \cdotp 3 = 3 \frac{\cos 3x}{\sin 3x} = 3 \cotg 3x
Dove alla fine abbiamo usato la definizione di cotangente di un angolo.
Esercizio 20. y= e^{ \ln^2 x }
Questo non è un esercizio semplice, però vi consiglio di provarci da soli e poi venire qui a vedere come si risolve! Suggerimento: partite dall’esterno verso l’interno.
Allora la prima funzione che troviamo è l’esponenziale. Quindi seguiamo la formula dell’esponenziale seguente come prima cosa.
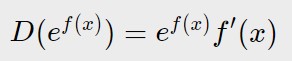
E quindi:
y' = e^{ \ln^2 x } \cdotp D(\ln^2 x)
Adesso cosa incontriamo prima? Potremmo dire il logaritmo no? Però quando ci sono degli esponenti in gioco (ln^2) riscriviamo il tutto come:
y' = e^{ \ln^2 x } \cdotp D( [\ln x]^2 )
E quindi come vedete in realtà la prima funzione esterna che incontriamo è quella di un qualcosa elevato alla alfa per il quale la formula l’abbiamo usata anche nell’esercizio 16.
y' = e^{ \ln^2 x } \cdotp 2\ln x \cdotp D( \ln x )
Adesso l’ultima funzione che incontriamo è quella di un logaritmo naturale semplice. Facciamone la derivata ed abbiamo concluso l’esercizio:
y' = e^{ \ln^2 x } \cdotp 2\ln x \cdotp \frac{1}{x} = \frac{2\ln x e^{ \ln^2 x } }{x}
Esercizio 21. y= \frac{1}{\ln^2 x}
Come detto nell’esercizio precedente è meglio quindi scrivere l’esponente come:
y= \frac{1}{ (\ln x)^2}
Poi, abbiamo visto nel capitoletto delle frazioni, che una frazione è meglio scriverla come potenza:
y= (\ln x)^{-2}
E quindi ci siamo ricondotti alla formula usata anche prima, cioè quella di una funzione f(x) elevata alla alfa. Iniziamo quindi ad usare tale formula e farne questa prima derivata:
y'= -2(\ln x)^{-3} \cdotp D(\ln x)
E poi incontriamo la funzione logaritmo naturale semplice all’interno sempre del D() chiaramente, quindi facciamone la derivata:
y'= -2(\ln x)^{-3} \cdotp \frac{1}{x} = \frac{-2}{x \ln^3 x}
Esercizio 22. y=x \sqrt{\ln^3 x } +4
Adesso non è un discorso di chi viene prima e chi viene dopo, semplicemente qui come prima cosa notiamo che abbiamo un prodotto di due funzioni (che abbiamo visto nel capitoletto di una derivata di un prodotto, quindi dobbiamo prima usare tale formula) :
f(x)=x
g(x)=\sqrt{\ln^3 x }
E poi abbiamo il 4 che nel momento in cui facciamo la derivata della somma se ne va via.
f'(x)=1
g'(x)=D(\sqrt{\ln^3 x })
La derivata g'(x) come vedete è una derivata di una funzione composta, e quindi possiamo adottare la politica di fare la derivata a strati per questa g'(x). Essendo non immediata la facciamo dopo, applichiamo la formula del prodotto innanzitutto:
y' = f'(x)g(x) + f(x)g'(x)
y' = \sqrt{\ln^3 x } + xg'(x)
Calcoliamo da parte g'(x) che non è immediato.
g'(x)=D(\sqrt{\ln^3 x })
Come detto nel capitoletto della derivata di una radice, è meglio scriverla sotto forma di potenza:
g'(x)=D(\ln^{\frac{3}{2} } x)
Portiamo l’esponente, come detto prima, nel modo seguente. In tal modo capiamo subito qual è la funzione più esterna:
g'(x)=D( [ \ln x ] ^{\frac{3}{2} })
Quindi dobbiamo prima fare la derivata di un qualcosa elevato alla alfa:
g'(x)= \frac{3}{2} \ln^{ \frac{3}{2} -1 } x \cdotp D(\ln x)
Adesso ci rimane da fare solo la derivata del logaritmo naturale semplice:
g'(x)= \frac{3}{2} \ln^{ \frac{1}{2} } x \frac{1}{x} = \frac{3}{2} \sqrt{\ln x} \frac{1}{x}
Adesso sostituiamo nella formula ed abbiamo concluso l’esercizio e trovato y’!
y' = \sqrt{\ln^3 x } + \frac{3}{2} \sqrt{\ln x}
Volendo possiamo anche mettere in evidenza ma non è necessario.
Esercizi derivate difficili
Esercizio 23. y= \frac{3 \sin 2x }{ 2 \cos x (1 + \sin^2 x) }
Prima di iniziare a fare derivate notiamo subito che possiamo semplificare il tutto, utilizzando la formula di duplicazione del seno:
\sin 2x = 2 \sin x \cos x
E quindi:
y= \frac{6 \sin x \cos x }{ 2 \cos x (1 + \sin^2 x) }
E possiamo levarci di mezzo il coseno:
y= \frac{3 \sin x }{1 + \sin^2 x}
A questo punto iniziamo a fare la derivata, usando la formula della derivata del quoziente di due funzioni.
y'= \frac{3 \cos x (1+ \sin^2 x) - 3 \sin x (2 \sin x \cos x) }{(1 + \sin^2 x)^2}
Svogliamo le parentesi:
y'= \frac{3 \cos x + 3 \cos x \sin^2 x - 6 \sin^2 x \cos x }{(1 + \sin^2 x)^2}
Sommiamo i termini comuni a numeratore:
y'= \frac{3 \cos x - 3 \cos x \sin^2 x }{(1 + \sin^2 x)^2}
Mettiamo in evidenza il 3 cos x:
y'= \frac{3 \cos x (1 - \sin^2 x ) }{(1 + \sin^2 x)^2}
All’interno della parentesi al numeratore, usando la prima relazione fondamentale della goniometria possiamo scrivere:
y'= \frac{3 \cos x \cos^2 x }{(1 + \sin^2 x)^2}
y'= \frac{3 \cos^3 x }{(1 + \sin^2 x)^2}
Come vedete le formule anche studiate in passato, soprattutto della goniometria, sono importantissime! Segnatevele!
Esercizio 24. y= \sqrt{ 1-x^2 } -x \arccos x
Abbiamo diverse cose insieme, derivata di una somma, di un prodotto, e di funzioni composte. Partiamo da sinistra verso destra lo stesso:
y'= D(\sqrt{ 1-x^2 }) - D(x \arccos x)
Nel primo caso facciamo la derivata della radice che sappiamo fare, nel secondo caso sfruttiamo la formula della derivata dell’arcocoseno che trovate in tabella come sempre.
y'= \frac{1}{2} (1 -x^2)^{- \frac{1}{2} } \cdotp D(1-x^2) - [\arccos x - \frac{x}{\sqrt{1-x^2} } ]
y'= - \frac{x}{\sqrt{1 -x^2} } -\arccos x + \frac{x}{\sqrt{1-x^2} }
Sommiamo i due termini opposti ed abbiamo concluso l’esercizio con la soluzione:
y'= -\arccos x
Esercizio 25. y=\ln \frac{ \sqrt{x^2 +1} +x }{ \sqrt{x^2 +1} -x }
La cosa che conviene fare in questo caso prima di iniziare a fare derivate è quella di sfruttare la relazione algebrica seguente:
[algeb]
E quindi andiamo a moltiplicare e dividere l’argomento del logaritmo per:
y=\ln \frac{ \sqrt{x^2 +1} +x }{ \sqrt{x^2 +1} -x } \cdotp \frac{\sqrt{x^2 +1} -x}{\sqrt{x^2 +1} -x}
In tal modo al numeratore abbiamo ottenuto la relazione sopra-scritta, mentre al denominatore un quadrato semplice. Quindi:
y=\ln \frac{ (\sqrt{x^2 +1})^2 -x^2 }{ (\sqrt{x^2 +1} - x)^2 }
y=\ln \frac{ x^2 +1 -x^2 }{ (\sqrt{x^2 +1} - x)^2 }
E quindi abbiamo semplificato la forma dell’argomento:
y=\ln \frac{1}{ (\sqrt{x^2 +1} - x)^2 }
Ora possiamo passare a fare la derivata a strati: partendo da sinistra troviamo il logaritmo.
y'=(\sqrt{x^2 +1} - x)^2 \cdotp D( \frac{1}{ (\sqrt{x^2 +1} - x)^2 } )
Poi troviamo una funzione fratta, scriviamola come potenza però, è più comodo:
y'=(\sqrt{x^2 +1} - x)^2 D( [\sqrt{x^2 +1} - x]^{-2} )
y'=(\sqrt{x^2 +1} - x)^2 \cdotp -2 [\sqrt{x^2 +1} - x]^{-3} \cdotp D( \sqrt{x^2 +1} - x )
Poi facciamo anche quell’altra derivata, e nel frattempo semplifichiamo gli esponenti.
y'= -2 [\sqrt{x^2 +1} - x]^{-1} \cdotp ( \frac{x}{\sqrt{x^2 +1}} - 1 )
y'= - \frac{2}{\sqrt{x^2 +1} - x} \cdotp ( \frac{x -\sqrt{x^2 +1} }{\sqrt{x^2 +1}} )
Metto un segno meno in evidenza (e levo quindi quello all’inizio), e scrivo il numeratore in parentesi nel modo seguente, così posso semplificare:
y'= \frac{2}{\sqrt{x^2 +1} - x} \cdotp ( \frac{ \sqrt{x^2 +1}-x }{\sqrt{x^2 +1}} )
y'= \frac{2}{\sqrt{x^2 +1}}
Abbiamo concluso questa lunga ma importantissima pagina sullo svolgimento degli esercizi derivate svolti!
Trovate altre centinaia di esercizi e argomenti sia di matematica che altro ancora! Continuate ad esercitarvi sul nostro sito!
Per approfondire:
https://it.wikipedia.org/wiki/Regole_di_derivazione
notevoli
esercizi
esercizi
svolti