Esercizi Disequazioni Esponenziali
Esercizi Disequazioni Esponenziali: 15 ESERCIZI svolti! In questa pagina saranno spiegati degli esercizi disequazioni esponenziali con tutti i passaggi spiegati passo dopo passo e con calma. La struttura e lo svolgimento degli esercizi è simile a quello delle equazioni esponenziali, che vi invito un attimo a vedere. Detto ciò iniziamo subito!
Indice
- Proprietà potenze
- Disequazioni esponenziali con base uguale
- Disequazioni esponenziali con base diversa
- Disequazioni esponenziali con sostituzione
Iniziamo subito a vedere le proprietà che ci serviranno durante questi esercizi, segnateveli!
Proprietà potenze

Iniziamo subito con gli esercizi disequazioni esponenziali svolti!
Esercizi Disequazioni Esponenziali con base uguale
Riassumiamo un attimo i passaggi fondamentali che andremo a seguire insieme.

Esercizio 1. 3^{2x} > 81
I passaggi sono bene o male gli stessi delle equazioni esponenziali, se non ve li ricordate li ripeteremo lo stesso passo dopo passo! Il PRIMO PUNTO è scrivere tutti i termini con stessa base. Nel nostro caso:
81=3 \cdotp 3 \cdotp 3 \cdotp 3 = 3^4
Abbiamo già stesse basi, ed è già soddisfatto anche il secondo punto, ossia avere una sola base (3) a sinistra ed una nell’altro membro a destra:
3^{2x} > 3^4
Ora per arrivare alla soluzione, seguiamo il TERZO PUNTO: mettere in disuguaglianza gli esponenti. Ossia scrivere SOLO gli esponenti con lo stesso segno della disequazione.
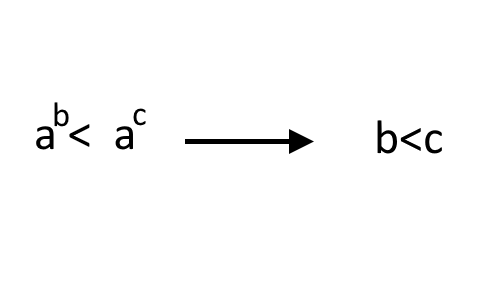
Nel nostro caso:
2x > 4
Abbiamo una equazione di primo grado, che sappiamo risolvere. Dividiamo per 2 tutto ed otteniamo:
x > \frac{4}{2}
Che sarebbe:
x > 2
L’esercizio è concluso!
Esercizio 2. 3^{2x +2 } < \frac{1}{3}
L’unica base da cambiare è la seconda, che sfruttando la quarta proprietà delle potenze, possiamo scrivere come:
\frac{1}{3} = 3^{-1}
E l’equazione diventa:
3^{2x +2 } < 3^{-1}
Le basi sono uguali adesso, e anche singole al primo membro ed al secondo. Possiamo ora mettere in disuguaglianza gli esponenti:
2x +2 < -1
Risolviamo questa equazione, portando il 2 a secondo membro innanzitutto:
2x < -1 -2
2x < -3
E poi dividendo per 2, abbiamo la soluzione della disequazione esponenziale:
x < - \frac{3}{2}
Esercizio 3. (\frac{3}{2})^x > \frac{27}{8}
Ricordiamo il primo punto: scrivere tutto con stessa base.
Anche in questo caso è possibile riscrivere il secondo termine:
\frac{27}{8} = \frac{3^3}{2^3}
E poi applicando la sesta proprietà delle potenze, possiamo scrivere questo come:
\frac{3^3}{2^3} = (\frac{3}{2})^3
E sostituendo tale risultato, notiamo che siamo riusciti a ricondurci ad una stessa base (primo punto).
(\frac{3}{2})^x > (\frac{3}{2})^3
Anche se una frazione, comunque sono basi uguali. Notiamo che la base 3:2= 1,5 che è maggiore di 1, quindi non cambia nulla; nell’esercizio successivo vedremo cosa succede se la base è minore di 1.
Mettiamo in disuguaglianza gli esponenti ed arriviamo alla soluzione immediata dell’esercizio:
x > 3
Continuiamo con altri esercizi disequazioni esponenziali !
Esercizio 4. (\frac{1}{27})^x > \frac{1}{81}
Scriviamo come sempre tutto nelle stesse basi, partiamo dal primo termine:
(\frac{1}{27})^x = (\frac{1}{3^3})^x
E poi applichiamo la terza proprietà delle potenze. E quindi il 3 va a moltiplicarsi con la x:
(\frac{1}{3^3})^x = (\frac{1}{3})^{3x}
Ora possiamo passare a riscrivere il secondo termine:
\frac{1}{81} = \frac{1}{3^4} = (\frac{1}{3})^4
(81 = 3^4 per il ragionamento fatto nel primo esercizio)
Sostituiamo il tutto nell’esercizio, ottenendo così:
(\frac{1}{3})^{3x} > (\frac{1}{3})^4
Ora per applicare il terzo punto c’è da stare attenti! Quando la base è più piccola di 1 come in questo caso:
1:3 = 0,333
Allora quando mettiamo in disuguaglianza gli esponenti, il segno della disequazione va invertito! Quindi:
3x < 4
Questo è molto importante, perchè a volte fate tutto bene e poi vi chiedete perchè non vi trovate. Questo può essere un motivo, segnatevelo!
Risolviamola dividendo per 3, ottenendo la seguente soluzione:
x < \frac{4}{3}
Esercizio 5. 9^{2x} > 1
Questo è un esercizio esemplare! L’1 a secondo membro è un Jolly! Cioè lo si può sempre scrivere come una qualsiasi base elevata alla zero, nel nostro caso ci serve la base 9 e quindi esso lo scriviamo come:
1=9^0
Abbiamo così:
9^{2x} > 9^0
Mettiamo in disuguaglianza gli esponenti ed il gioco è fatto!
2x > 0 \implies x > 0
Esercizio 6. 4 \cdotp 2^{3x} - 4^{x+2} < 0
PRIMO PUNTO: ricondurre a stessa base il tutto. Facciamo una cosa alla volta: partiamo da sinistra a destra, e quindi con il primo 4.
2^2 \cdotp 2^{3x} - 4^{x+2} < 0
Poi il secondo 4 lo possiamo scrivere come:
4^{x+2} =(2^2)^{x+2} =2^{2(x+2)} = 2^{2x+4}
dove è stata applicata la terza proprietà delle potenze. Sostituiamo nell’equazione ricavando:
2^2 \cdotp 2^{3x} - 2^{2x+4} < 0
Il primo punto è finito: avere tutto in stessa base.
Adesso vediamo il secondo punto: avere una sola base a sinistra e destra. Iniziamo a portare l’ultimo termine a secondo membro:
2^2 \cdotp 2^{3x} < 2^{2x+4}
Il problema qui è a primo membro, che abbiamo due basi ancora. Applichiamo quindi la prima proprietà delle potenze unendo i due termini e scriviamo quindi:
2^{3x+2} < 2^{2x+4}
Ora che la forma è quella giusta, passiamo al punto tre: mettere in disuguaglianza gli esponenti.
3x+2 < 2x+4
Portiamo le x da una parte e i numeri dall’altra:
3x-2x < 4-2
\implies x < 2
Continuiamo con altri esercizi disequazioni esponenziali con base diversa!
Esercizi Disequazioni Esponenziali con base diversa
Esercizio 7. 2^x < \frac{ 7^{x+1} }{2}
Qui abbiamo dei termini esponenziali con la x con diversa base, analogamente alle equazioni esponenziali, il trucco per la risoluzione di questi tipi di equazioni è quello di ricondurre tutto prima ad uno stesso esponente e poi cercare di avere stesse basi. Quindi la differenza è che qui c’è un primo passaggio in più.
Vediamolo subito che capiamo meglio!
Partiamo con lo scomporre il 7 per comodità:
2^x < \frac{ 7 \cdotp 7^x }{2}
Il primo passo è quello di raggruppare i termini con stesso esponente. Quindi dividiamo tutto per 7^x:
\frac{ 2^x }{ 7^x } < \frac{ 7 }{2}
Ora applichiamo la sesta proprietà delle potenze e quindi il primo termine diventa:
(\frac{2}{7})^x < \frac{ 7 }{2}
Il secondo punto è quello di cercare di avere la stessa base del termine esponenziale con la x.
Qui basta applicare la quarta proprietà delle potenze al secondo termine:
(\frac{2}{7})^x < (\frac{2}{7})^{-1}
Abbiamo quindi come nel caso precedente di disequazioni esponenziali, una stessa base: e quindi possiamo mettere in disuguaglianza gli esponenti. ATTENZIONE però se la base è più piccola di 1, allora si deve cambiare il segno della disequazione!
\implies x > -1
Esercizio 8. 16 \cdotp 4^{2x} < 3^{x+1}
I termini esponenziali (con la x ) hanno diversa base. Qui se seguiamo alla perfezione gli stessi passaggi di prima non riusciamo ad arrivare alla soluzione. Questo perchè dobbiamo arrivare ad avere stessi esponenti. Quindi facciamo come segue:
4^{2x} = (4^2)^x = 16^x
E così abbiamo un altro 16, e quindi possiamo applicare la prima proprietà delle potenze e moltiplicare i due termini.
16 \cdotp 16^x < 3^{x+1}
Segue che:
16^{x+1} < 3^{x+1}
Come vedete abbiamo ottenuto stessi esponenti, quindi prima di iniziare a risolvere, cercate di notare sempre come è fatta l’equazione!
Ora dividiamo tutto per 3^{x+1}:
\frac{16^{x+1} }{3^{x+1} }< 1
E da qui in poi è come nell’esercizio precedente: quindi applichiamo sempre la sesta proprietà delle potenze ed il primo termine diventa:
(\frac{16}{3})^{x+1} < 1
L’1 è come detto tante volte un jolly, di fatti lo possiamo scrivere come una qualsiasi base elevata alla zero:
(\frac{16}{3})^{x+1} < (\frac{16}{3})^0
E siamo arrivati al secondo punto, ossia quello di avere stesse basi. Il gioco è fatto!
x+1 < 0 \implies x < -1
Continuiamo con altri esercizi disequazioni esponenziali con sostituzione!
Esercizi Disequazioni Esponenziali con sostituzione
Esercizio 11. 3^x - 2 \cdotp 3^{ 2-x } < 7
Analogamente alle equazioni esponenziali risolvibili con sostituzione, quando notiamo che il termine esponenziale ha la stessa base allora si può procedere per sostituzione. Con termine esponenziale intendiamo quello con la x per intenderci. In questo caso i due termini con la x hanno la stessa base (3), degli altri non ci interessa.
Iniziamo a scomporre il secondo termine esponenziale con la x:
3^x - 2 \cdotp 3^2 \cdotp 3^{-x} < 7
Scriviamolo come frazione, che è più comodo:
3^x - 2 \cdotp 3^2 \cdotp \frac{1}{3^x} < 7
Ora possiamo procedere con una sostituzione. Come vedete ci disinteressiamo di tutti gli altri termini. Poniamo infatti:
3^x = z
E quindi otteniamo:
z - 2 \cdotp 3^2 \cdotp \frac{1}{z} < 7
Ossia una disequazione fratta, se non ve le ricordate cliccateci sopra e ripetetele un attimo, almeno i passaggi da seguire in generale.
Come prima cosa calcoliamo le condizioni di esistenza, ossia denominatore diverso da zero.
CE: z \ne 0
Poi andiamo ad ottenere la forma seguente:
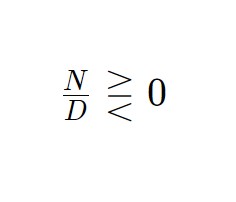
z - 2 \cdotp 3^2 \cdotp \frac{1}{z} - 7 < 0
Adesso andiamo a fare il minimo comune multiplo:
\frac{z^2 -18 -7z }{z} < 0
Ed andiamo a risolvere un falso sistema per arrivare a degli intervalli di soluzione.
\big\| z^2 -18 -7z <0 \\ \big\| z < 0
Il secondo termine è apposto, prendiamo il primo termine un attimo da parte.
z^2 -18 -7z <0
z^2 -7z -18 <0
Essa è una disequazione di secondo grado, calcoliamo quindi il discriminante:
\Delta = b^2 - 4ac = 49 + 72 = 121
Delta>0 e disequazione con segno di minore (<) e quindi calcoliamo le singole soluzioni e poi prendiamone i valori interni. (Cliccateci un attimo sopra nella pagina delle disequazioni di secondo grado per vedere la tabella molto comoda). Calcoliamo le soluzioni singole:
z_{1,2} = \frac{-b \pm \sqrt{ \Delta } }{2a} = \frac{7 \pm 11 }{2}
E quindi:
z_1 = \frac{7+11}{2} = 9
z_2 = \frac{7-11}{2} = -2
La soluzione è i valori interni, quindi:
-2 < z < 9
Sostituiamo questo dato nel falso sistema iniziale:
\big\| -2 < z < 9 \\ \big\| z < 0
Con il quadro dei segni, prendiamo l’intervallo negativo perchè la disequazione dell’esercizio ha un segno di minore.
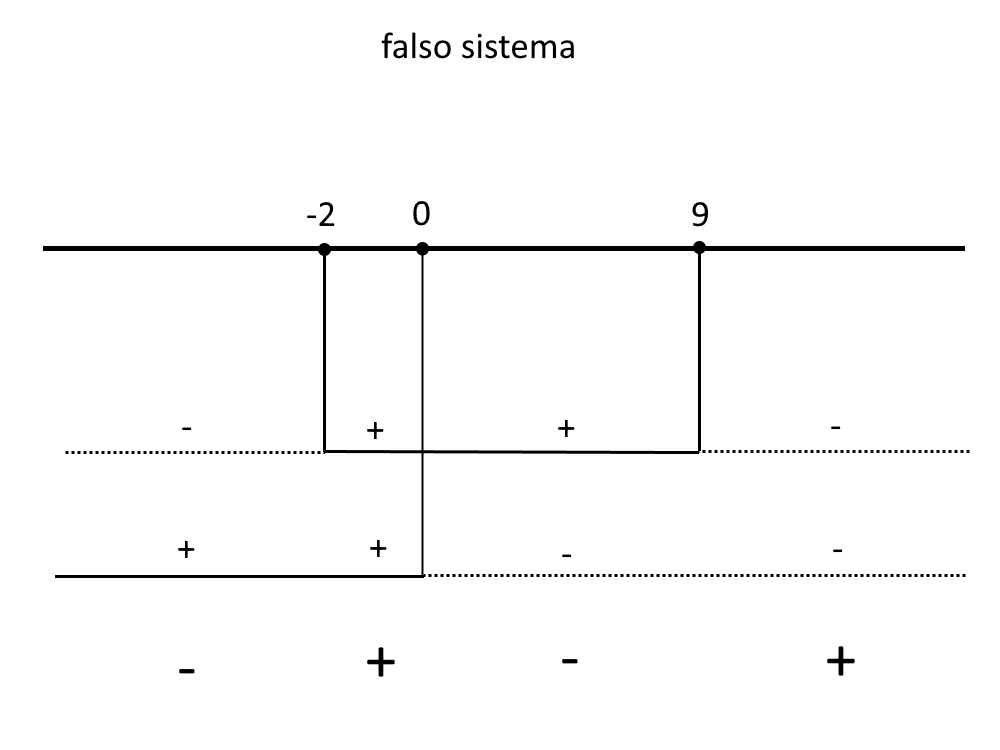
z<-2 \lor 0<z<9
Ora dobbiamo ritornare alla variabile x iniziale:
z<-2 la scartiamo perchè è impossibile, visto che:
3^x < -2 e visto che è un esponenziale che per definizione è positivo, è impossibile che sia più piccolo di -2.
Per 0<3^x<9 risolviamo il sistema:
\begin{cases} 0 < 3^x \\ 3^x < 9 \end{cases}
\begin{cases} 3^x > 0 \\ 3^x < 9 \end{cases}
Essendo un esponenziale per definizione positivo, esso è sicuramente maggiore di 0.
\begin{cases} \forall x \\ 3^x < 3^2 \end{cases}
Il secondo termine lo sappiamo risolvere, sarebbero gli esponenziali con stessa base e quindi mettiamo in disuguaglianza gli esponenti.
\begin{cases} \forall x \\ x<2 \end{cases}
E la soluzione finale dell’esercizio è x<2 !
Esercizio 12. 2 \cdotp 3^{-x} - 3^x \ge 1
Scriviamo il termine esponenziale come frazione, così facilitiamo la sostituzione successiva.
2 \frac{1}{3^x} - 3^x \ge 1
Ora siamo in grado di sostituire, come vedete i termini esponenziali sono addirittura uguali. Poniamo:
z = 3^x
Quindi l’equazione dell’esercizio diventa in questa nuova variabile:
2 \frac{1}{z} - z \ge 1
Questa è ancora una volta una disequazione fratta, quindi per la risoluzione facciamo innanzitutto le condizioni d’esistenza e ci leviamo il pensiero.
CE: z \ne 0
Ora possiamo decidere se moltiplicare tutto per z, oppure fare il minimo comune multiplo. Conviene assolutamente in questi casi moltiplicare tutto per z, che è più veloce:
2 - z^2 \ge z
- z^2 -z +2\ge 0
Abbiamo una disequazione di secondo grado, quindi innanzitutto cambiamo tutto di segno ( e quindi anche il segno stesso della disequazione) e calcoliamo il delta.
z^2 +z -2 \le 0
\Delta = b^2 - 4ac = 1 + 8 = 9
Delta>0 quindi esiste soluzione. Calcoliamo le singole soluzioni come se fosse una equazione normale di secondo grado, e poi prendiamone i valori interni (essendo la disequazione col minore).
z_{1,2} = \frac{-b \pm \sqrt{ \Delta } }{2a} = \frac{-1 \pm 3 }{2}
E così::
z_1 = \frac{-1+3}{2} = 1
z_2 = \frac{-1-3}{2} = -2
Essendo la disequazione col minore, prendiamo i valori interni:
-2 \le z \le 1
Qui intervengono le CE, perchè ci dicono che dobbiamo scartare z=0. Quindi riscriviamo scartando z=0:
-2 \le z < 0 \lor 0 < z \le 1
L’intervallo di soluzione -2 \le z < 0 lo scartiamo perchè z è un esponenziale e non può essere mai più piccolo di zero, essendo per definizione positivo. Quindi concentriamoci sulla seconda soluzione 0<z \le 1 , e ritorniamo alla variabile x.
0 < 3^x \le 1
Valori interni e valori esterni si risolvono con un sistema così come vedete:
\begin{cases} 3^x > 0 \\ 3^x \le 1 \end{cases}
\begin{cases} 3^x > 0 \\ 3^x \le 3^0 \end{cases}
Il primo termine è un esponenziale ed è sempre positivo.
\begin{cases} \forall x \\ x \le 0 \end{cases}
E visto che in un sistema prendiamo i valori comuni, allora la soluzione dell’esercizio è proprio x \le 0 !
Continuiamo con altri esercizi disequazioni esponenziali !
Esercizio 13. -4^x - 3 \cdotp 2^x > 2^{2x} - 2^x
Scriviamo i termini esponenziali con la x in stessa base, con le proprietà visti già negli esercizi precedenti, ossia solo il termine con base 4.
-2^{2x} - 3 \cdotp 2^x > 2^{2x} - 2^x
Possiamo tranquillamente già passare al cambiamento di variabile. Poniamo:
z= 2^x
La nostra equazione diventa:
-z^2 - 3 z> z^2 - z
Portiamo tutto a primo membro.
-z^2 - 3 z- z^2 + z > 0
-2z^2 - 2z > 0
Abbiamo ancora una volta una disequazione di secondo grado. Prima di tutto cambiamo di segno tutto per avere tutto positivo. Ricordatevi che quando si cambia tutto di segno una disequazione si cambia anche il segno stesso della disequazione!
2z^2 + 2z < 0
Piuttosto che calcolare il discriminante ecc., è più veloce mettere in evidenza una z:
z(2z + 2) < 0
Per risolvere questo prodotto si risolve un falso sistema.
z(2z + 2) < 0
\big\| z<0 \\ \big\| 2z +2 0
Ossia:
\big\| z<0 \\ \big\| z < -1
Prendiamo gli intervalli col segno – (essendo la disequazione con un minore < ) nel quadro dei segni:
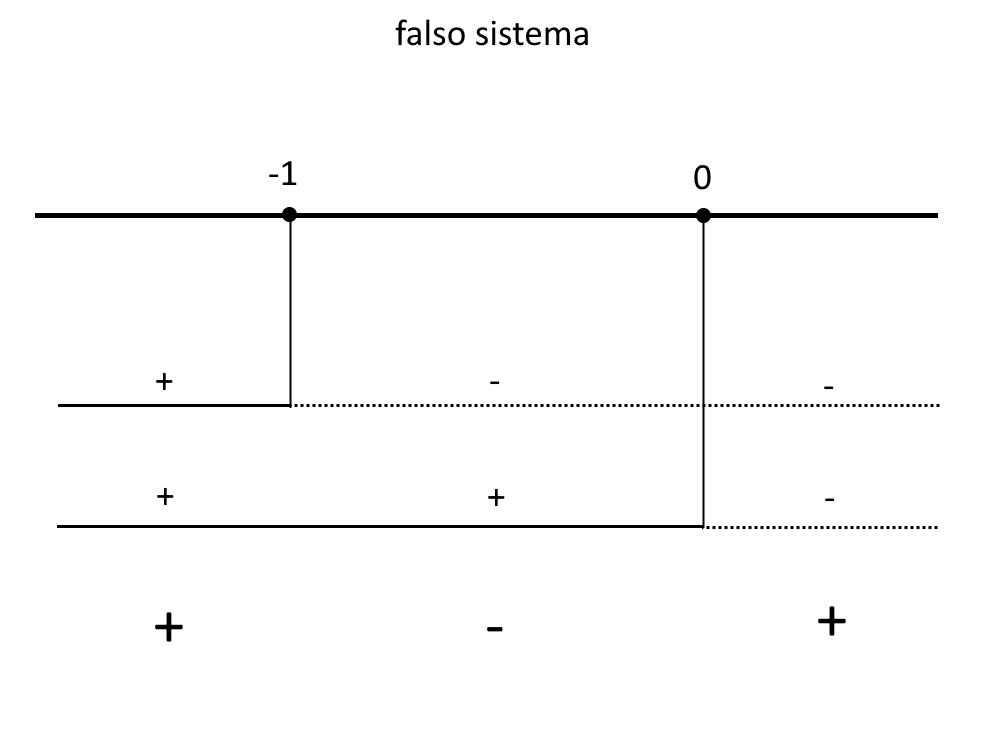
-1 < z < 0
Ritorniamo alla variabile iniziale adesso.
-1 < 2^x < 0
Essendo un esponenziale per definizione positivo (>0) non può mai essere più piccolo di zero, quindi non esiste soluzione.
Esercizio 14. \frac{1}{ 3^x - 9 } - \frac{1}{ 3^x + 1 } > 0
Come potete notare abbiamo due termini esponenziali uguali, possiamo subito andare ad effettuare una sostituzione!
z=3^x
L’equazione diventa nella nuova variabile:
\frac{1}{ z - 9 } - \frac{1}{ z + 1 } > 0
Essa è una disequazione fratta, quindi effettuiamo le condizioni di esistenza innanzitutto, ossia denominatori diversi da zero.
CE: z- 9 \ne \implies z \ne 9
CE: z +1 \ne 0 \implies z \ne -1
Facciamo il minimo comune multiplo:
\frac{z+1 - (z-9)}{ (z-9)(z + 1) } > 0
\frac{10}{ (z-9)(z + 1) } > 0
Ora ragioniamo un attimo: tutto questo deve essere >0, cioè positivo. Il numeratore 10 è ovviamente positivo, quindi basterà che anche il denominatore sia positivo per far sì che il tutto sia >0.
Risolviamo solamente:
(z-9)(z + 1) > 0
Questo è un prodotto in una disequazione, e si risolve con un falso sistema:
\big\| z-9>0 \\ \big\| z+1 > 0
\big\| z>9 \\ \big\| z > -1
Facciamo uno schema dei segni, e prendiamo la parte con il segno + (essendoci un > maggiore nella disequazione). Quindi:
z < -1 \lor z > 9
Le CE sono già incluse, quindi non dobbiamo scartare nulla.
Ora dobbiamo ripassare alla variabile iniziale x!
3^x < -1 \lor 3^x > 9
La prima soluzione la scartiamo ovviamente perchè il termine esponenziale non può essere negativo. Il secondo lo risolviamo come abbiamo fatto tante volte già:
3^x > 3^2 \implies x > 2
Esercizio 15. \frac{-6}{ 2^x - 2 } + \frac{9}{ 2^x - 1 } < 0
Come nell’esercizio precedente, possiamo subito fare una bella sostituzione:
z=2^x
Abbiamo una disequazione fratta simile all’esercizio 14! Provate a risolverla da soli e poi venite a vedere la soluzione!
\frac{-6}{ z - 2 } + \frac{9}{ z - 1 } < 0
Iniziamo con le condizioni di esistenza dei denominatori.
CE: z-2 \ne 0 \implies z \ne 2
CE: z-1 \ne 0 \implies z \ne 1
Adesso passiamo a fare il minimo comune multiplo e ridurre tutto in una forma compatta.
\frac{ -6(z-1) + 9 (z-2) }{ (z - 2)(z-1) } < 0
\frac{ -6z +6 + 9z - 18 }{ (z - 2)(z-1) } < 0
Sommiamo i rispettivi termini simili.
\frac{ 3z - 12 }{ (z - 2)(z-1) } < 0
Ora siamo nelle condizioni di risolvere questa disequazione con un falso sistema:
\big\| 3z - 12 < 0 \\ \big\| (z - 2)(z-1) < 0
\big\| 3z < 12 \\ \big\| (z - 2)(z-1) < 0
Il primo termine è risolvibile molto facilmente, dividiamo per 3:
\big\| z < 4 \\ \big\| (z - 2)(z-1) < 0
Il secondo termine è una disequazione con prodotto, quindi lo svolgiamo con un altro falso sistema fatto a parte, e poi andiamo a sostituire il risultato. Quindi facciamo un attimo da parte:
\big\| z-2 < 0 \\ \big\| z-1 < 0
\big\| z < 2 \\ \big\| z < 1
Con un quadro dei segni, prendendo la parte col segno – (essendoci un minore nella disequazione presa) abbiamo:
1<z<2
Sostituiamo questo nel falso sistema base, e risolviamolo finalmente:
\big\| z < 4 \\ \big\| 1<z<2
Con un quadro dei segni, prendendo gli intervalli col segno -, abbiamo che la soluzione è:
z<1 \lor 2<z<4
Queste rispettano anche le CE. Ora è arrivato il momento di risostituire ed avere la soluzione nella variabile x iniziale. Ricordiamo che:
z=2^x
Risolviamo un termine alla volta: partiamo dal primo.
2^x < 1
2^x < 2^0 \implies x < 0
Ed abbiamo trovato la prima soluzione. Passiamo al secondo termine, quando vedete dei valori interni o esterni si risolvono con un sistema:
\begin{cases} 2^x > 2 \\ 2^x < 4 \end{cases}
\begin{cases} 2^x > 2^1 \\ 2^x < 2^2 \end{cases}
Ed abbiamo:
\begin{cases} x>1 \\ x < 2 \end{cases}
Visto che è un sistema, e nel sistema si prendono i valori comuni, ossia 1<x<2 come in figura.
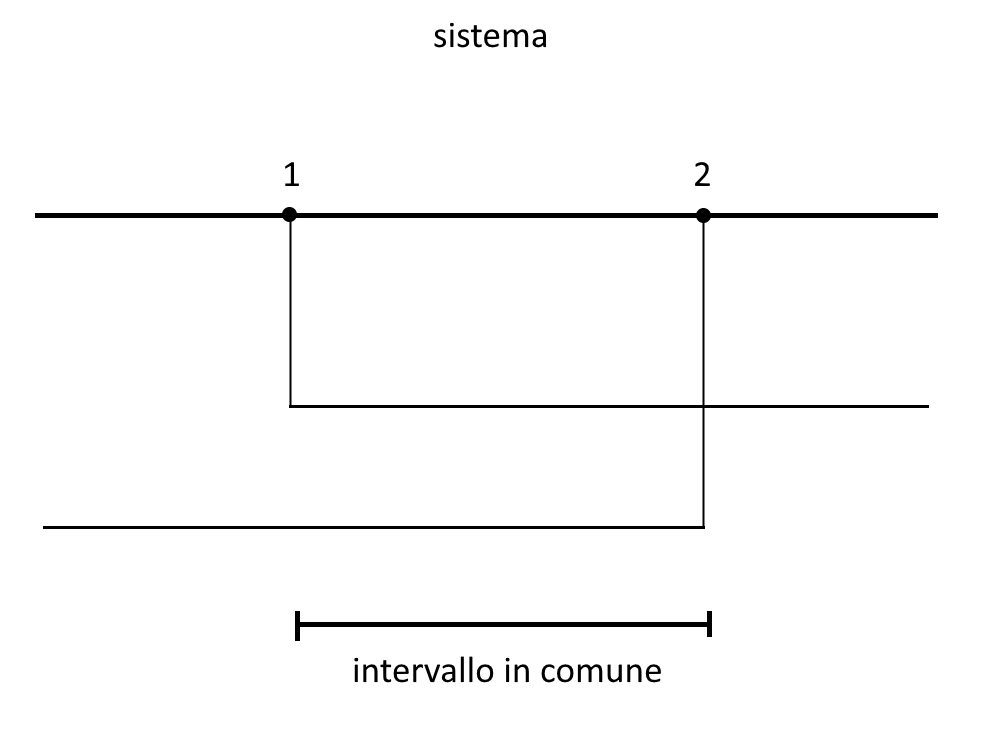
E quindi unendo anche la soluzione di prima abbiamo:
x < 0 \lor 1<x<2
In questa pagina abbiamo visto come risolvere gli esercizi disequazioni esponenziali. Inoltre abbiamo visto che per essere pronti al meglio, è importante sapere o comunque dare un’occhiata sulle equazioni esponenziali. Nel corso degli esercizi ci si trova di fronte anche a disequazioni fratte e disequazioni di secondo grado!
Trovate altre centinaia di esercizi su questo sito sia di matematica che altro ancora!
Per approfondire:
https://it.wikipedia.org/wiki/Disequazione_esponenziale
esponenziali
esercizi
numero in
logaritmo